«ХАИ»
Интерполирование для таблиц с постоянным шагом
Цель: для функции, заданной таблично, найти приближённое значение в точках x1, x2, x3 и значение производной в точке x4.
Вычислительная схема:
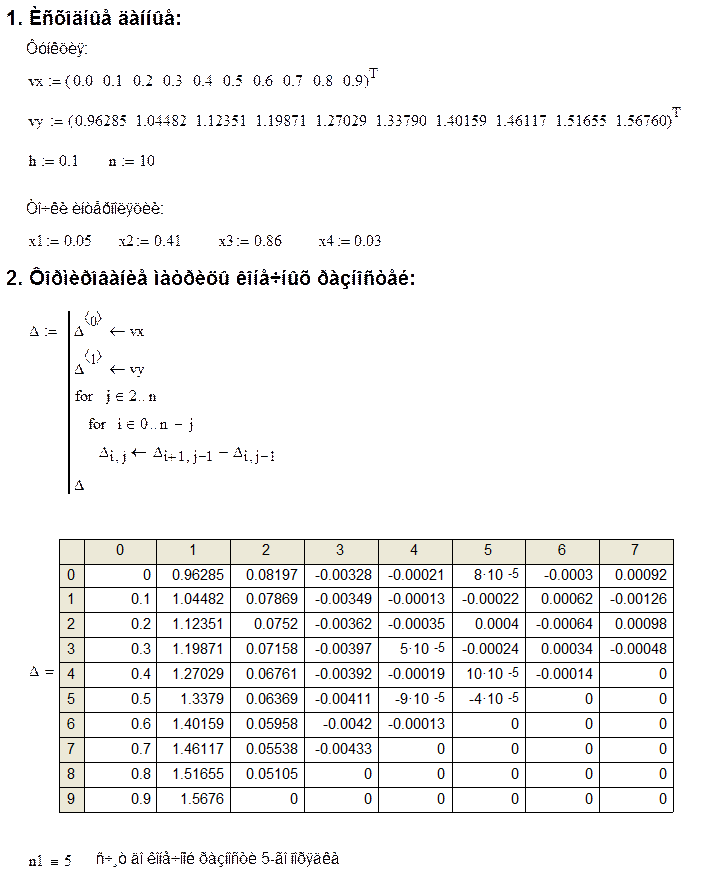
1. Составление таблицы конечных разностей:
Пусть таблица ![]() задана с постоянным
шагом
задана с постоянным
шагом ![]()
Конечной разностью 1-го порядка называется
![]()
Конечной разностью n-го порядка называется
![]()
Конечные разности записываются в виде таблицы или треугольной матртцы:

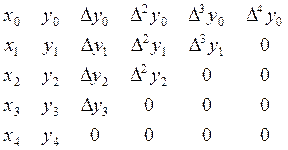
2. Первая интерполяционная формула Ньютона:
![]()
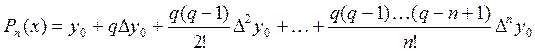 ,
,
![]()
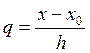
![]() Формула
используется для интерполирования в начале таблицы.
Формула
используется для интерполирования в начале таблицы.
![]() Погрешность
для первой интерполяционной формулы Ньютона:
Погрешность
для первой интерполяционной формулы Ньютона:
![]()
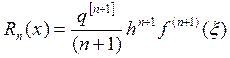 ,где xÎ(
,где xÎ(![]() ,
,![]() ) и
) и
![]()
![]()
![]()
3. Вторая
интерполяционная формула Ньютона:![]()
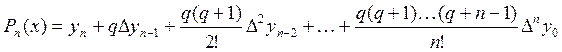 ,
,
![]()
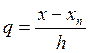
![]() Формула
используется для интерполирования в конце таблицы.
Формула
используется для интерполирования в конце таблицы.
![]() Погрешность
для второй интерполяционной формулы Ньютона:
Погрешность
для второй интерполяционной формулы Ньютона:
![]()
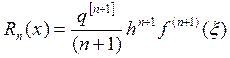 ,где xÎ(
,где xÎ(![]() ,
,![]() ) и
) и
![]()
![]()
![]()
4. Интерполяционная формула Гаусса:
Пусть точка интерполирования ![]() лежит в середине таблицы между узлами
интерполяции
лежит в середине таблицы между узлами
интерполяции ![]() и
и ![]() :
:
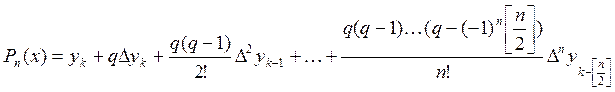 ,
,
![]()
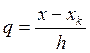
Погрешность для интерполяционной формулы Гаусса:
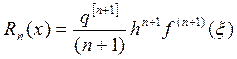 ,где xÎ(
,где xÎ(![]() ,
,![]() )
и
)
и
![]()
![]()
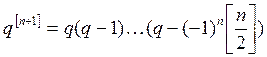
5. Численное дифференцирование:
Для нахождения производной ![]() функцию
функцию ![]() приблизительно
заменяем интерполяционным полиномом, построенным на узлах
приблизительно
заменяем интерполяционным полиномом, построенным на узлах ![]() ,¼,
,¼,![]() ,
, ![]() :
:
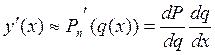
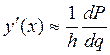
Погрешность численного дифференцирования
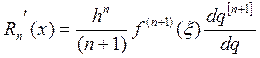
6. Обратное интерполирование:
Задача сводится к нахождению аргумента по заданному значению функции. Для решения задачи используется метод последовательных приближений.
Пусть точка ![]() лежит в
середине таблицы между узлами интерполяции
лежит в
середине таблицы между узлами интерполяции ![]() и
и ![]()
Приведём уравнение
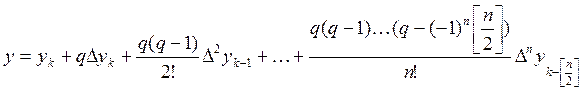
к виду ![]() :
:
 ,
,
В качестве начального приближения выбираем:

![]()
Продолжая процесс итераций, получим:
![]()
Процесс итераций продолжаем до тех пор, пока не установятся цифры заданной точности и получим
![]() .
.
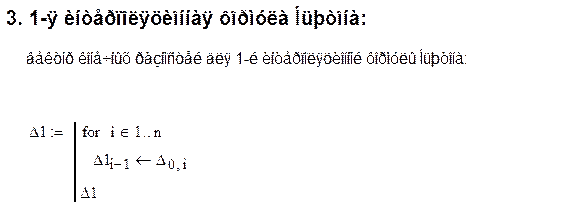
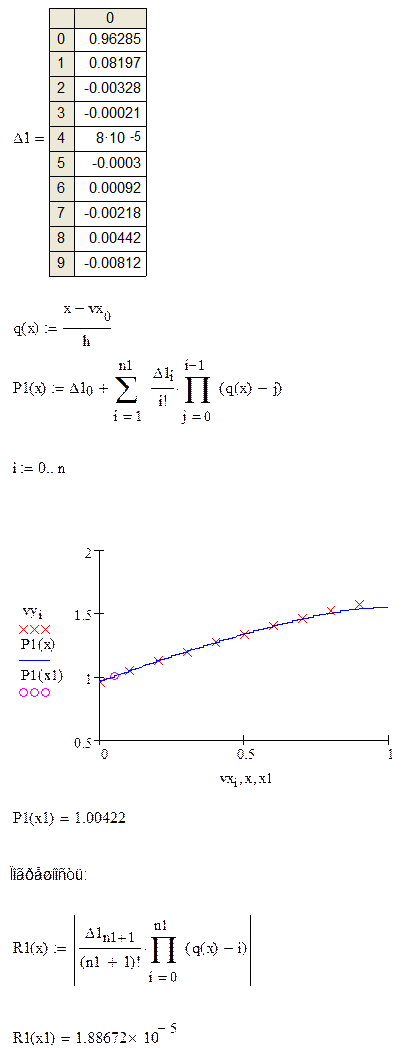


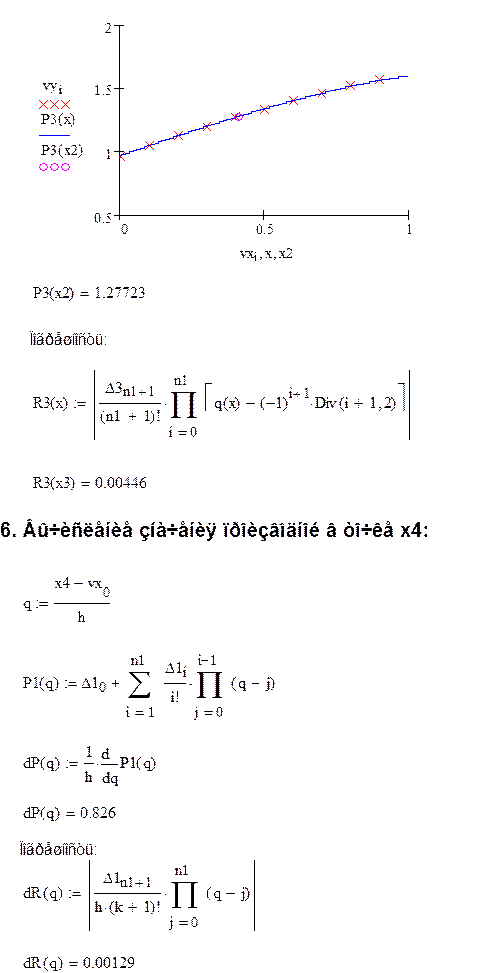
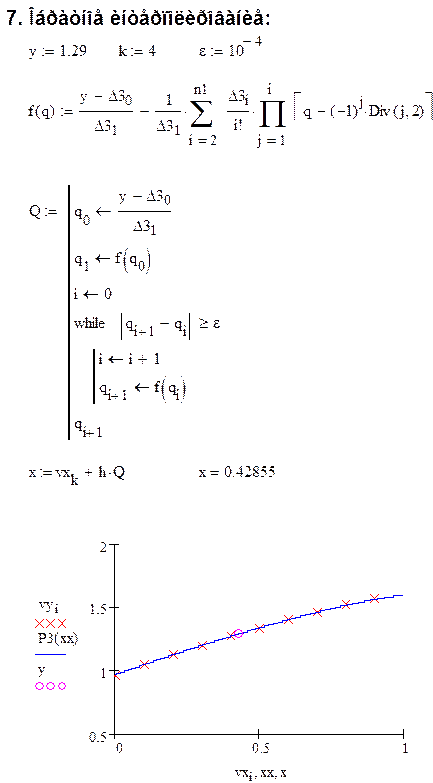
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.