«ХАИ»
Решение алгебраических и трансцендентных уравнений методом итераций
Цель: методом
итераций вычислить приближённодействительный корень заданного
уравнения. Вычисления проводить до тех пор, пока два последовательных
приближения (![]() и
и ![]() )
удовлетворят неравенству
)
удовлетворят неравенству ![]() .
.
Вычислительная схема:
1. Графически найти интервал изоляции корня для заданного уравнения
2. Проверка уравнения на сходимость итерационного процесса:
Для сходимости итерационного процесса, достаточно
исходное уравнение ![]()
привести к виду ![]() так,
чтобы выполнялось условие
так,
чтобы выполнялось условие
![]()
при ![]() .
.
3. Приведение уравнения к виду пригодному для использования метода итераций:
Для этого уравнение ![]() заменяется
равносильным
заменяется
равносильным ![]() . В этом случае
. В этом случае
![]() . Параметр
. Параметр ![]() выбираем так, чтобы
выбираем так, чтобы ![]() при
при ![]() ,
,
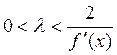 .
.
4. Решение уравнения методом итераций:
Пусть дано уравнение ![]() ,
, ![]() -
интервал изоляции корня.
-
интервал изоляции корня.
Приводим данное уравнение к виду
![]() (1)
(1)
, где ![]() - некоторая непрерывная на отрезке
- некоторая непрерывная на отрезке ![]() функция.
функция.
Выбираем произвольное ![]() и
подставляем его в правую часть равенства (1):
и
подставляем его в правую часть равенства (1):
![]() .
.
Аналогично получаем:
![]() ,
,
![]() ,
,
¼
![]() .
.
Доказано, что если последовательность ![]() ,
, ![]() , ¼,
, ¼, ![]() ,¼ сходиться, то её пределом является корень уравнения
,¼ сходиться, то её пределом является корень уравнения ![]() , а значит, и корень уравнения
, а значит, и корень уравнения ![]() , так как эти два уравнения равносильны.
, так как эти два уравнения равносильны.
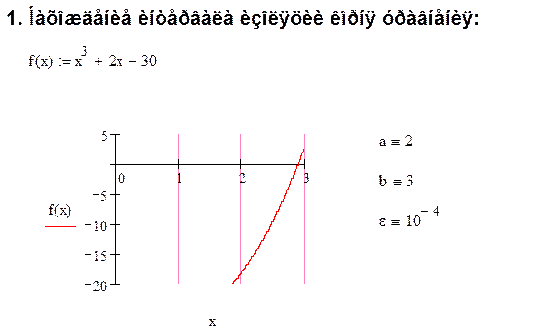
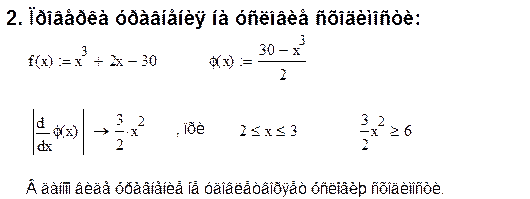
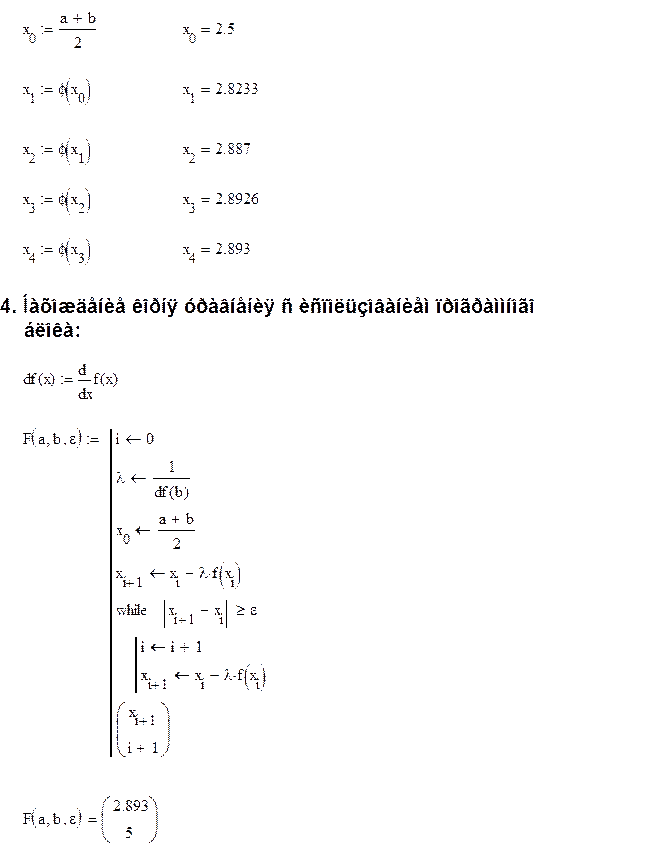
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.