





«ХАИ»
Решение систем линейных алгебраических уравнений методом Гаусса
Цель: используя метод Гаусса (схему единственного деления), решить заданную систему из
трёх уравнений с тремя неизвестными.
Вычислительная схема:
Если ![]() - матрица коэффициентов,
- матрица коэффициентов, ![]() -
матрица свободных членов и
-
матрица свободных членов и
![]() , то
, то
![]()
Его структура следующая:
Given – начало блока;
тело блока – несколько конструкций вида АВ1 операция АВ2;
FIND (список) или MINERR (список) – конец блока;
АВ1, АВ2 – арифметические выражения либо константы;
операция – некоторая операция отношения.
список – перечень переменных, которые необходимо найти.
С помощью FIND ищут точное решение. Если оно отсутствует, то возникает ошибка.
Посредством MINERR всегда будет найдено решение, минимизирующее невязку
ограничений. Встроенная переменная ERR содержит величину ошибки.
Перед решающим блоком необходимо задать начальные условия для всех искомых
переменных (можно в векторном виде), соответственно в теле решающего блока
можно использовать запись уравнений в матричном виде
4. Решение систем уравнений методом Гаусса:
Пусть дана система линейных уравнений:
![]()
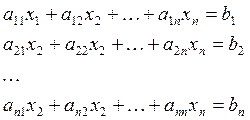
где ![]() ij – коэффициенты системы, xj –
неизвестные, bi – свободные члены.
ij – коэффициенты системы, xj –
неизвестные, bi – свободные члены.
1. Предположим
![]() (ведущий элемент). Всё первое уравнение
поделим на
(ведущий элемент). Всё первое уравнение
поделим на
ведущий элемент:
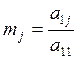 (
(![]() )
)
2. Последовательно
исключаем неизвестное ![]() из каждого
из каждого ![]() -го
уравнения (
-го
уравнения (![]() )
)
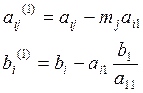 (
(![]() ),(
),(![]() )
)
Преобразованная система будет иметь вид:
![]()
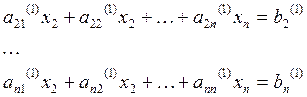
3. Продолжая
процесс, исключаем ![]() .Получаем систему из
.Получаем систему из ![]() -х
уравнений.
-х
уравнений.
На некотором ![]() -м
шаге получим:
-м
шаге получим:
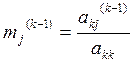
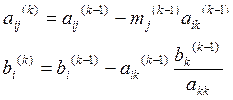
,
где ![]() ,
, ![]() ,
, ![]()
При ![]() происходит
исключение
происходит
исключение ![]() неизвестного из последнего уравнеия.
неизвестного из последнего уравнеия.
Окончательно получаем уравнение, которым заканчивается прямой ход:
![]()
Получим треугольную систему:

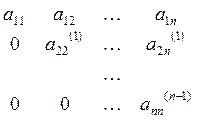
4. Обратный ход- решение полученной системы с помощью процесса подстановки:
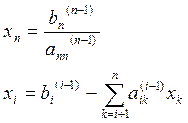 ,
, ![]()
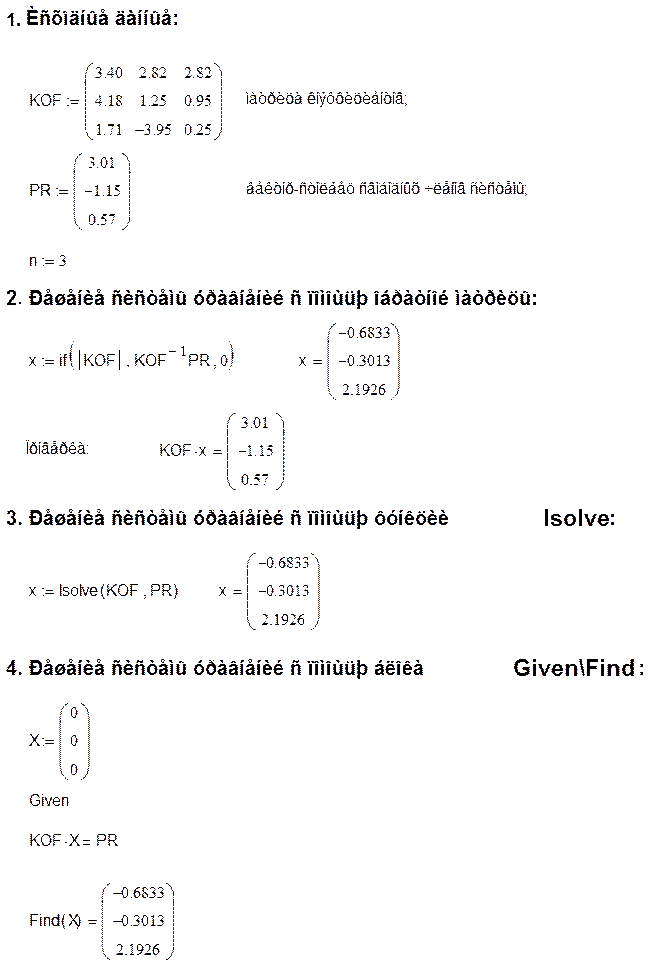
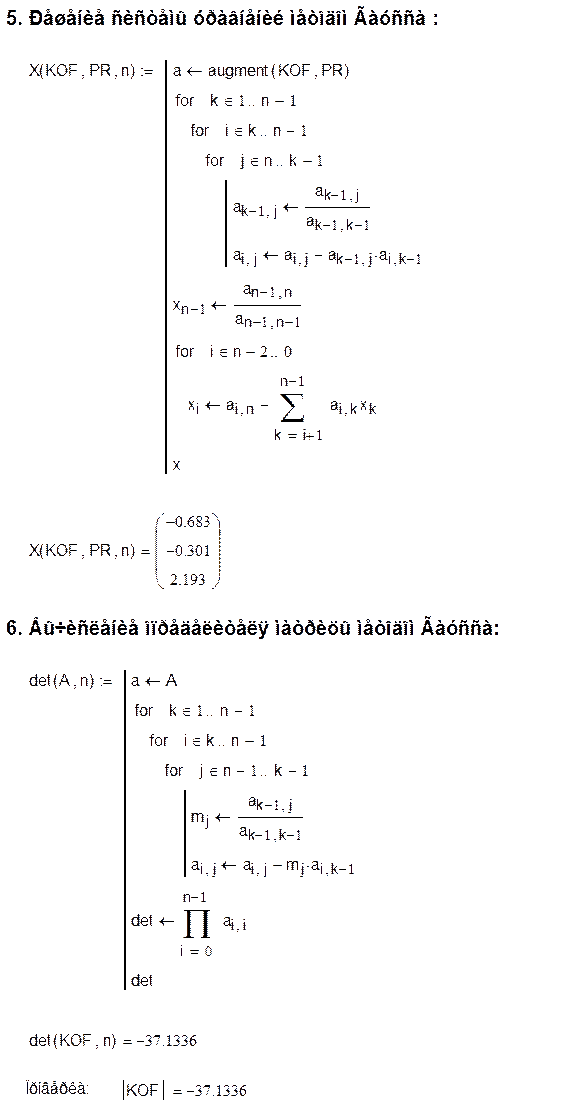
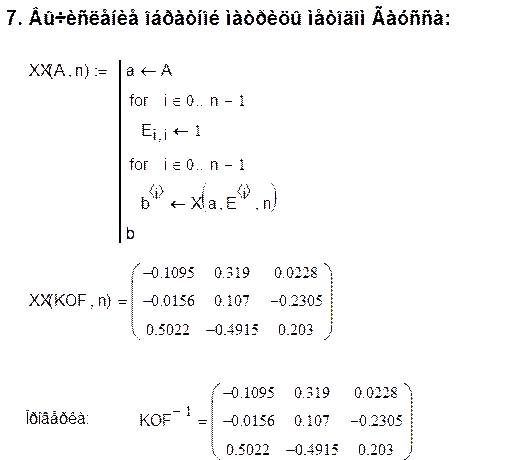
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.