Министерство образования науки
Национальный аэрокосмический университет
им. Н.Е. Жуковского
кафедра 304
Лабораторная работа №8
по предмету
«Численные методы»
Выполнила студентка
Группы 325
Абкеримова Рушена
Проверила: преподаватель кафедры 304
Яровая Ольга Владимировна
Харьков 2014
Построение кубических сплайнов
Вариант №1
|
x |
1.4 |
1.8 |
2.3 |
2.9 |
3.2 |
3.6 |
|
y |
0.3365 |
0.5878 |
0.8329 |
1.0647 |
1.1632 |
1.2809 |
Цель работы: построить кубический сплайн для функции, заданной таблично. Для этого найти шаги, матрицы A,H,M. Данное задание выполнить в пакетах Matlab, Mathcad. В обоих пакетах вывести график. Сравнить полученные результаты. Также проверять себя можно сравнивая значение функции и значение кубического сплайна в одной точке(они должны совпадать).
Mathcad
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Matlab
function res=gaus(a)
x(2)=0;
x(3)=0;
x(4)=0;
for k=4:-1:1;
d=0;
for j=2:4;
d=d+a(k,j)*x(j);
end;
x(k)=a(k,5)-d;
end;
x(5)=0;
x(6)=0;
for k=1:6;
m(k+1)=x(k);
end;
for k=1:6;
res(k)=m(k);
end;
function A = MatrA(h,Y)
for i=1:4;
for j=1:4;
if j==i;
A(i,j)=(h(i)+h(i+1))/3;
end;
if j==i+1;
A(i,j)=h(i+1)/6;
end;
if j==i-1;
A(i,j)=h(i)/6;
end;
A(i,5)=Y(i);
end;
end;
function H = MatrH(h)
for i=1:4;
for j=1:6;
H(i,j)=0;
if j==i ;
H(i,j)=1/h(i);
end;
if j==i+1;
H(i,j)=-(1/h(i)+1/h(i+1));
end;
if j==i+2
H(i,j)=1/h(i+1);
end;
end;
end;
function res=PrivedMatrA(a)
for k=1:4;
for i=k+1:5;
for j=5:-1:1;
b(k,j)=a(k,j)/a(k,k);
res(k,j)=b(k,j);
if i<=4;
a(i,j)=a(i,j)-a(i,k)*b(k,j);
end;
end;
end;
end;
function Y = ProizvedMatr(H,f)
for i=1:4;
sum=0;
for k=1:6;
sum=sum+H(i,k)*f(k);
end;
Y(i)=sum;
end;
function g = Splain(xx,X,h,m,f,k)
g=m(k-1)*((power((X(k)-xx),3)/(6*h(k-1))))+m(k)*(power(xx-X(k-1),3)/(6*h(k-1)))+(f(k-1)-(m(k-1)*((power(h(k-1),2)/6))))*((X(k)-xx)/h(k-1))+(f(k)-m(k)*(power(h(k-1),2)/6))*((xx-X(k-1))/h(k-1));
function h = Stolbech(x)
for i=1:5
h(i)=x(i+1)-x(i);
end;
Результат:
>> X=[1.4 1.8 2.3 2.9 3.2 3.6]
X =
1.4000 1.8000 2.3000 2.9000 3.2000 3.6000
>> f=[0.3365 0.5878 0.8329 1.0647 1.1632 1.2809]
f =
0.3365 0.5878 0.8329 1.0647 1.1632 1.2809
>> Stolbech(X)
ans =
0.4000 0.5000 0.6000 0.3000 0.4000
>> h=ans
h =
0.4000 0.5000 0.6000 0.3000 0.4000
>> MatrH(h)
ans =
2.5000 -4.5000 2.0000 0 0 0
0 2.0000 -3.6667 1.6667 0 0
0 0 1.6667 -5.0000 3.3333 0
0 0 0 3.3333 -5.8333 2.5000
>> H=ans
>> ProizvedMatr(H,f)
ans =
-0.1380 -0.1039 -0.0580 -0.0341
>> Y=ans
>> MatrA(h,Y)
ans =
0.3000 0.0833 0 0 -0.1380
0.0833 0.3667 0.1000 0 -0.1039
0 0.1000 0.3000 0.0500 -0.0580
0 0 0.0500 0.2333 -0.0341
>> A=ans
>> PrivedMatrA(A)
ans =
1.0000 0.2778 0 0 -0.4602
0 1.0000 0.2911 0 -0.1907
0 0 1.0000 0.1846 -0.1437
0 0 0 1.0000 -0.1200
>> MatrA=ans
>> Gaus(MatrA)
ans =
0 -0.4170 -0.1553 -0.1215 -0.1200 0
>> m=ans
>> x1=1.4:0.01:1.8;
>> x2=1.8:0.01:2.3;
>> x3=2.3:0.01:2.9;
>> x4=2.9:0.01:3.2;
>> x5=3.2:0.01:3.6;
>> plot(X,f,'x',x1,Splain(x1,X,h,m,f,2),'r',x2,Splain(x2,X,h,m,f,3),'g',x3,Splain(x3,X,h,m,f,4),'b',x4,Splain(x4,X,h,m,f,5),'black',x5,Splain(x5,X,h,m,f,6),'c')
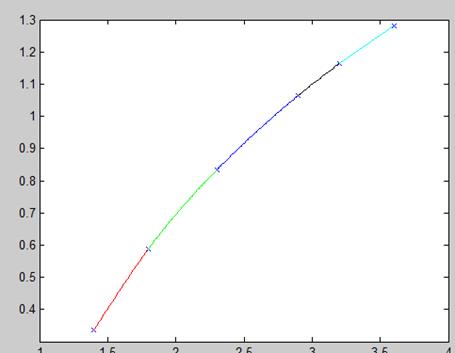
Нахождение матрицы М через обратную матрицу:
function res=Work(X,Y);
%---------------------------
n=size(X);
n=n(2);
for i=1:n-1
h(i)=X(i+1) - X(i);
end;
H1=zeros(n-2,n);
A=zeros(n-2,n-2);
for i=1:n-2
H1(i,i)= 1/h(i);
H1(i,i+1)=-(1/h(i)+1/h(i+1));
H1(i,i+2)=1/h(i+1);
end;
for i=1:n-2
A(i,i)= (h(i)+h(i+1))/3;
if (i~=1) A(i,i-1)= h(i)/6;
end;
if (i~=(n-2)) A(i,i+1)= h(i+1)/6;
end;
end;
S=H1*Y;
M=A\S;
M1=zeros(n,1);
for i=1:n-2
M1(i+1)=M(i);
end;
res=M1;
return
>> x=[1.4, 1.8, 2.3, 2.9, 3.2, 3.6];
>> y=[0.3365; 0.5878; 0.8329; 1.0647; 1.1632; 1.2809];
>> M=Work(x,y)
M =
0
-0.4170
-0.1553
-0.1215
-0.1200
0
Скрипт-файл:
function rts = script2(A,B,eps)
choise = questdlg('Выберите метод нахождения матрицы М:','Методы', 'Метод прогонки','Через обратную матрицу','Точки');
x=[1.4, 1.8, 2.3, 2.9, 3.2, 3.6];
y=[0.3365; 0.5878; 0.8329; 1.0647; 1.1632; 1.2809];
switch choise
case 'Метод прогонки'
Gaus(MatrA);
case 'Через обратную матрицу'
M=Work(x,y);
end
end
>> x=[1.4, 1.8, 2.3, 2.9, 3.2, 3.6];
>> y=[0.3365; 0.5878; 0.8329; 1.0647; 1.1632; 1.2809];
>> script2
M =
0
-0.4170
-0.1553
-0.1215
-0.1200
0
Вывод: была выполнена вся работа, поставленная преподавателем. Научились находилась находить кубические сплайны для функции , заданной таблично. Ответы, полученные в разных математических пакетах, а также вычисления проведенные разными способами сошлись с небольшой погрешностью, которая, в некоторых случаях, могла произойти в результате округления чисел при делении. В целом лабораторная работа была выполнена, поставленные цели достигнуты
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.