заметания используют две основные структуры данных:
Список точек событий – последовательность абсцисс, упорядоченных слева направо и определяемых позициями «остановок» заметающей прямой.
Статус заметающей прямой – подходящее описание пересечения этой прямой с набором заданных отрезков. Статус заметающей прямой должен обновляться в точках событий, и представляющая статус структура данных должна выбираться, исходя из требуемых операций анализа и обновления статуса.
Состояние относительно выметающей прямой описывает соотношения между объектами, пересекаемыми выметающей прямой.
Таблица точек-событий — это последовательность координат х, упорядоченных слева направо, в которой определяются точки останова выметающей прямой. Каждая такая точка останова называется точкой-событием. Состояние относительно выметающей прямой определяется только в точках-событиях [2].
Предположим, что заданы N интервалов на действительной оси и необходимо узнать, не перекрываются ли какие-нибудь два из них. Ответ можно получить за время O(N2), проверив все пары интервалов, но тут же на ум приходит намного лучший алгоритм, основанный на сортировке. Если упорядочить 2N концевых точек этих интервалов и обозначить их как левые (Л) или правые (П), то эти интервалы не перекрываются тогда и только тогда, когда концы их образуют чередующуюся последовательность: Л, П, Л, П, ..., П, Л, П . Эту проверку можно провести за O(N logN) времени.
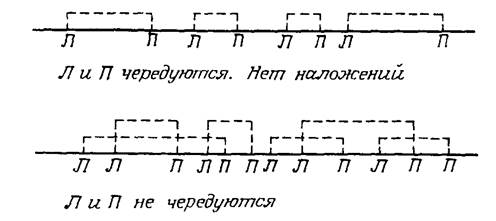
Рисунок 1.1 - Определение наложений интервалов
Заданный набор из N
действительных чисел {![]() } можно преобразовать в набор из N
интервалов {[
} можно преобразовать в набор из N
интервалов {[![]() ]} за линейное время. Эти интервалы
перекрываются тогда и только тогда, когда исходные числа не уникальны, и это
доказывает следующую теорему:
]} за линейное время. Эти интервалы
перекрываются тогда и только тогда, когда исходные числа не уникальны, и это
доказывает следующую теорему:
Теорема. Для того чтобы определить, перекрываются ли N интервалов, необходимо и достаточно Q(N logN) сравнений, при условии что можно использовать лишь алгебраические функции на входе [1].
Теперь посмотрим, что
происходит на самом деле при сортировке для выявления наложений. Мотивом для
этого исследования служит отсутствие естественного полного упорядочения
отрезков на плоскости, поэтому на обобщение, основанное только на сортировке,
не приходится рассчитывать. Однако если мы сможем понять существенные черты
одномерного алгоритма, то нам удастся обобщить его и на плоский случай. Два
интервала перекрываются тогда и только тогда, когда они содержат хотя бы одну
общую точку. Каждая точка на действительной оси связана с множеством, состоящим
из накрывающих ее интервалов. Это соответствие определяет функцию С: R→ ![]() , отображающую действительные числа
на подмножества множества {1, ..., N}. Значение функции С может меняться только
на множестве из 2N концевых точек заданных интервалов. Если мощность {С(х)}
превышает мощность последнего множества, то интервалы перекрываются. Чтобы
обнаружить это, отсортируем концы интервалов и создадим простейшую структуру
данных, состоящую всего лишь из одного целого числа, т. е. числа интервалов,
накрывающих текущую абсциссу.
, отображающую действительные числа
на подмножества множества {1, ..., N}. Значение функции С может меняться только
на множестве из 2N концевых точек заданных интервалов. Если мощность {С(х)}
превышает мощность последнего множества, то интервалы перекрываются. Чтобы
обнаружить это, отсортируем концы интервалов и создадим простейшую структуру
данных, состоящую всего лишь из одного целого числа, т. е. числа интервалов,
накрывающих текущую абсциссу.
Просматривая концы отрезков слева направо, вставляем интервал в эту структуру данных в тот момент, когда встречен его левый конец, и удаляем его в момент встречи правого конца. Всякая попытка вставить в структуру, в которой уже хранится число один, свидетельствует о наложении; в противном случае наложений нет. Поскольку обработка каждой концевой точки при таком подходе занимает лишь константное время, то процесс проверки (после сортировки) требует не более чем линейного времени.
Рассмотрим пару
непересекающихся отрезков ![]() и
и ![]() на плоскости. Будем считать, что
на плоскости. Будем считать, что ![]() и
и ![]() сравнимы в абсциссе х, если
существует такая вертикаль, проходящая через х, которая пересекает оба
отрезка. Введем отношение выше в х следующим образом:
сравнимы в абсциссе х, если
существует такая вертикаль, проходящая через х, которая пересекает оба
отрезка. Введем отношение выше в х следующим образом: ![]() выше
выше ![]() в х (пишется
в х (пишется
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.