Приближенное вычисление интегралов. Формулы Чебышева и Гаусса

кафедра 304

Лабораторная работа № 12

по предмету «Численные методы»

по теме: «Приближенное вычисление интегралов.

Формулы Чебышева и Гаусса»

Выполнила студентка 325 гр.

Старцева А. В.

Проверила  ст. преподаватель каф. 304

Яровая О. В.

______________________

Теоретические сведенья

Теоретические сведенья

Теоретические сведенья

Таблица   для формулы

N	i
2	1;2
3	1;3 2
4	1;4 2;3
5	1;5 2;4 3
6	1;6 2;5 3;4
7	1;7 2;6 3;5 4

Чебышева                                                         Гаусса

n	i
1	1
3	1;3 2		5/9 8/9
4	1;4 2;3
5	1;5 2;4 3

Ручной счет

N			)
1
2
3
4

N			)	A
1
2
3
4

Расчет в пакете Mathcad

Формула Чебышева

Формула Гаусса

Погрешность

Расчет в пакете Matlab

function res = Cheb(func, a, b, n, T)

S=0;

h=(b-a)/n;

for i=1:1:n

    S= S+f1(func,((a+b)/2+(b-a)/2*T(n-1,i)));

end;

res=h*S;

function res = Gauss(f, a, b, n, A, Tg)

S = 0;

h=(b-a)/2;

for i=1:1:n-1

    S=S+A(n-1,i)*f1(f,((a+b)/2+(b-a)/2*Tg(n-1,i)));

end;

res=h*S;

function res = f1(func, a)

syms x

res = double(subs(func, x, a));

function res = ReadFile(file)

res=dlmread(file);

function res = Rn(func, a, b, n)

res=( (b-a)^(2*n+1) * prod(1:n)^4 * ...

    (f1(func, (b-a)/2))^(2*n) )/ ( prod(1:2*n)^3 * (2*n+1) );

function res = CH()

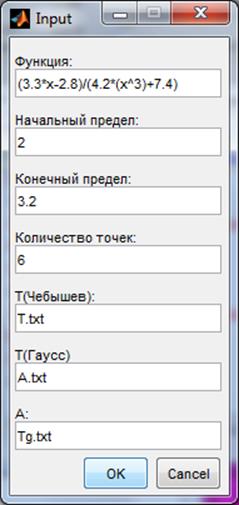
prompt = {'Функция:','Начальный предел:','Конечный предел:', 'Количество точек:', '"T"(Чебышев):', '"A":', '"T"(Гаусс)'};

dlg_title = 'Input';

num_lines = 1;

def = {'(3.3*x-2.8)/(4.2*(x^3)+7.4)','2','3.2', '6', 'T.txt', 'A.txt', 'Tg.txt'};

answer = inputdlg(prompt,dlg_title,num_lines,def);

func = answer{1};

a = str2num(answer{2});

b = str2num(answer{3});

n = str2num(answer{4});

T = ReadFile(answer{5});

A = ReadFile(answer{6});

Tg = ReadFile(answer{7});

results{1} = 'Результат:';

results{2} = strcat('Методом Чебышева: ',num2str(Cheb(func, a, b, n, T),'%.8f'));

results{3} = strcat('Методом Гаусса: ', num2str(Gauss(func, a, b, n, A, Tg),'%.8f'));

results{4} = strcat('Погрешность: ', num2str(Rn(func, a, b, n),'%.15f'));

choise = questdlg(results,'Интегрирование методом Чебышева и Гаусса', 'Показать график функции', 'Выход', 'Показать график функции');

if(choise(1)=='П') 

    fplot(func,[a,b]);

end;

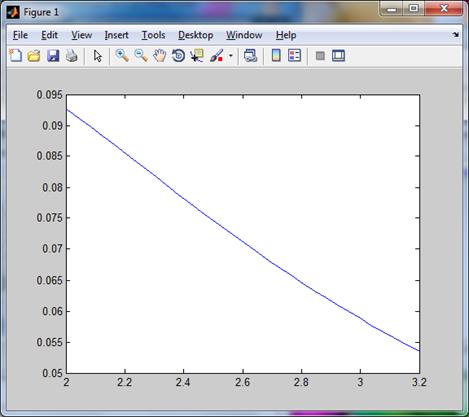
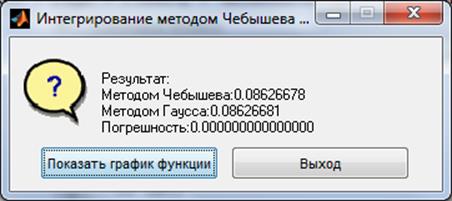
Вывод: на этой лабораторной работе я научилась находить приближенное значение определенного интеграла 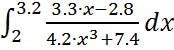    на заданном интервале [2, 3.2]  с помощью формулы Чебышева и Гаусса при заданном числе промежутков интегрирования n=6  с помощью пакетов Mathcad (0.08627; 0.08627) и  Mathlab (0.086266; 0.086266). А так же научилась оценивать погрешность вычисления.