1. Метод
линейной интерполяции (метод хорд). Пусть дано уравнение ![]() , где функция
, где функция ![]() непрерывна
на [a;b] и f(a)f(b)<0. Для определенности положим f(a)>0 и f(b)<0.
Тогда, вместо того чтобы делить отрезок [a;b] пополам (как это делается в
методе половинного деления), более естественно поделить его в отношении
f(a)/f(b). Это дает приближенное значение корня x1=b+h1,
где
непрерывна
на [a;b] и f(a)f(b)<0. Для определенности положим f(a)>0 и f(b)<0.
Тогда, вместо того чтобы делить отрезок [a;b] пополам (как это делается в
методе половинного деления), более естественно поделить его в отношении
f(a)/f(b). Это дает приближенное значение корня x1=b+h1,
где
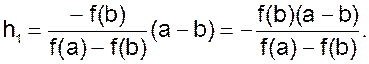
Далее, применив этот прием к тому из отрезков ([a;x1] или [x1;b]), на концах которого функция f(x) имеет противоположные знаки, получим второе приближение корня x2 и т.д.
Геометрически способ пропорциональных частей эквивалентен замене кривой y = f(x) хордой, проходящей через точки A(a;f(a)) и B(b;f(b)) ( рис. 2.1).
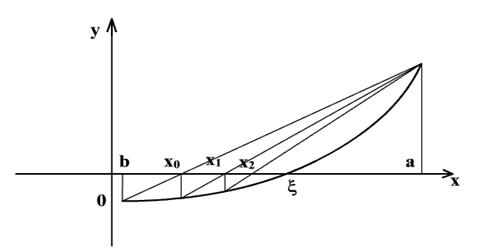
Рис. 2.1. Геометрическая интерпретация метода хорд
В самом деле,
уравнение хорды AB есть 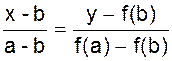 .
.
Отсюда, полагая x=x1 и y=0,
получаем 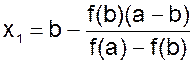 .
.
Для сходимости метода хорд необходимо, чтобы выполнялись следующие условия:
а) неподвижен тот конец хорды, для которого знак функции f(x) совпадает со знаком ее второй производной f”(x);
б) последовательные приближения xn лежат по ту сторону корня ξ, где функция f(x) имеет знак, противоположный знаку ее второй производной f”(x).
Расчетная формула метода в случае неподвижной точки a:
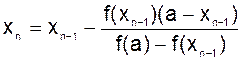 .
.
Если отрезок [a;b] достаточно мал, то погрешность метода определяется так:
![]()
![]() .
.
Таким образом, в
этом случае, как только будет выполняться условие ![]() , где ε
– заданная предельная абсолютная погрешность, гарантировано, что
, где ε
– заданная предельная абсолютная погрешность, гарантировано, что ![]() .
.
2.
Метод Ньютона (метод касательных). Пусть ![]() –
корень уравнения
–
корень уравнения ![]() – отделен на отрезке [a, b],
причем
– отделен на отрезке [a, b],
причем ![]() и
и ![]() непрерывны
и сохраняют определенные знаки при
непрерывны
и сохраняют определенные знаки при ![]() .
.
Положим![]() , где
, где ![]() считаем
малой величиной. Отсюда, применив формулу Тейлора, получим
считаем
малой величиной. Отсюда, применив формулу Тейлора, получим
0 = ![]() .
.
Следовательно,
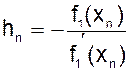 .
.
Внеся эту поправку в формулу уточнения корня, можно найти следующее (по порядку) приближение корня:
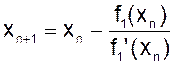 ( n = 0, 1, 2, . . .).
( n = 0, 1, 2, . . .).
Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой y = f(x) касательной, проведённой в некоторой точке кривой (рис. 2.2).
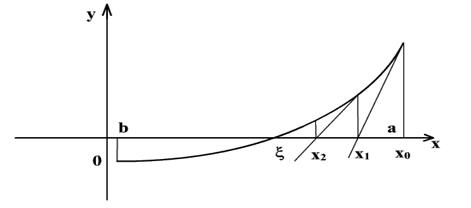
Рис. 2.2. Геометрическая интерпретация метода Ньютона
Теорема. Если ![]() , причем
, причем ![]() и
и ![]() отличны от нуля и сохраняют определенные
знаки при
отличны от нуля и сохраняют определенные
знаки при ![]() , то, исходя из начального приближения
, то, исходя из начального приближения ![]() , удовлетворяющего неравенству
, удовлетворяющего неравенству ![]() , можно вычислить методом Ньютона
, можно вычислить методом Ньютона
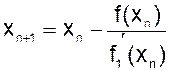
единственный корень ![]() уравнения
уравнения
![]() с любой степенью точности.
с любой степенью точности.
Применяя метод
Ньютона, следует руководствоваться следующим правилом: в качестве исходной
точки ![]() выбирается тот конец интервала
выбирается тот конец интервала ![]() , которому отвечает ордината того же знака,
что и знак
, которому отвечает ордината того же знака,
что и знак ![]() .
.
Условием завершения
итерационного процесса является выполнение неравенства ![]() ,
где ε – заданная предельная абсолютная погрешность.
,
где ε – заданная предельная абсолютная погрешность.
3.
Модифицированный метод Ньютона. Если производная f’(x) мало изменяется на
отрезке [a, b], то в расчетной формуле метода касательных можно положить ![]() ≈
≈![]() .
.
Отсюда для корня ![]() уравнения f(x) = 0 получаем
последовательные приближения
уравнения f(x) = 0 получаем
последовательные приближения
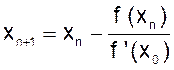 ( n = 0, 1, 2, . . .).
( n = 0, 1, 2, . . .).
Геометрически этот
способ означает, что заменяются касательные в точках Bn[xn,
f(xn)] прямыми, параллельными касательной к кривой y = f(x), в её
фиксированной точке B0[x0, f(x0)] (рис. 2.3).
Эта формула весьма полезна, если ![]() сложна.
сложна.
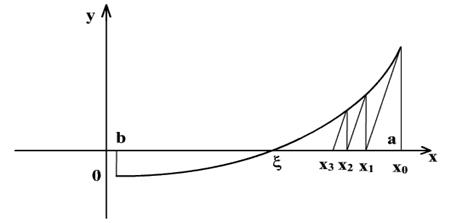
Рис. 2.3. Геометрическая интерпретация модифицированного
метода Ньютона
4. Метод
секущих. В алгоритме Ньютона требуется вычислить две функции для каждой
итерации – ![]() и
и ![]() . Метод
секущих требует только одного вычисления функции
. Метод
секущих требует только одного вычисления функции ![]() при
одной итерации, и простой корень имеет порядок сходимости R
при
одной итерации, и простой корень имеет порядок сходимости R![]() 1,618033989. Этот метод почти так же быстр,
как и метод Ньютона, который имеет порядок сходимости R=2.
1,618033989. Этот метод почти так же быстр,
как и метод Ньютона, который имеет порядок сходимости R=2.
В методе секущих
используется такая же формула, как и в методе хорд, но существуют различные
логические решения относительно способа поиска каждого последующего члена.
Необходимо около точки ![]() иметь две начальные точки
иметь две начальные точки ![]() и
и ![]() , как
показано на рис. 2.4. Определим
, как
показано на рис. 2.4. Определим ![]() как абсциссу точки
пересечения линии, проходящей через эти две точки
как абсциссу точки
пересечения линии, проходящей через эти две точки
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.