«ХАИ»
Интерполяционный многочлен Лагранжа
Цель:
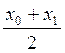 ,
,
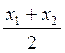 ,
, 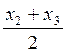 .
.Вычислительная схема:
1. Интерполяция данных кубическими сплайнами с помощью встроенной функции interp:
Кубическая сплайн-интерполяция позволяет провести кривую через заданные точки так, чтобы первые и вторые ее производные были непрерывны в каждой точке. Для аппроксимации данных при помощи кубических сплайнов существует функция interp(s,x,y,z), где s - вектор, содержащий значения вторых производных сплайна в экспериментальных точках, x,y - векторы с соответствующими координатами опытных точек, z - переменная, от которой будет зависеть создаваемая функция.
Вектор s , содержащий значения вторых производных интерполяционной кривой в заданных точках, можно вычислить, используя одну из функций, которые отличаются лишь граничными условиями:
lspline (vx, vy) – генерация сплайна, приближающегося в граничных точках к прямой линии;
pspline (vx, vy) – генерация сплайна, приближающегося в граничных точках к параболе;
cspline (vx, vy) – генерация сплайна, приближающегося в граничных точках к кубической параболе.
2. Построениеинтерполяционного полинома Лагранжа :
Многочлен Лагранжа имеет вид:
![]()
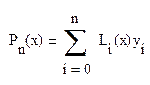
Лагранжевый коэффициент
![]()
![]()
определим как многочлен степени n, который обращается в 0, во всех точках, кроме
![]()
![]()
Константу А определим из условия:
![]()
Тогда
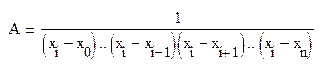
и
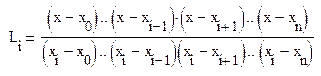
Если ввести обозначения :
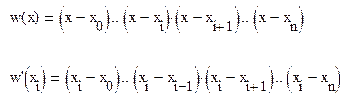
то
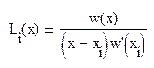 .
.
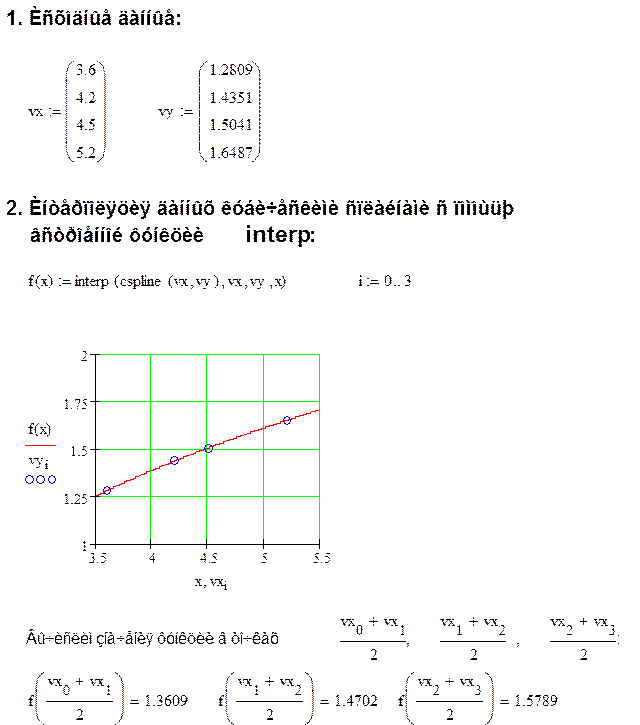
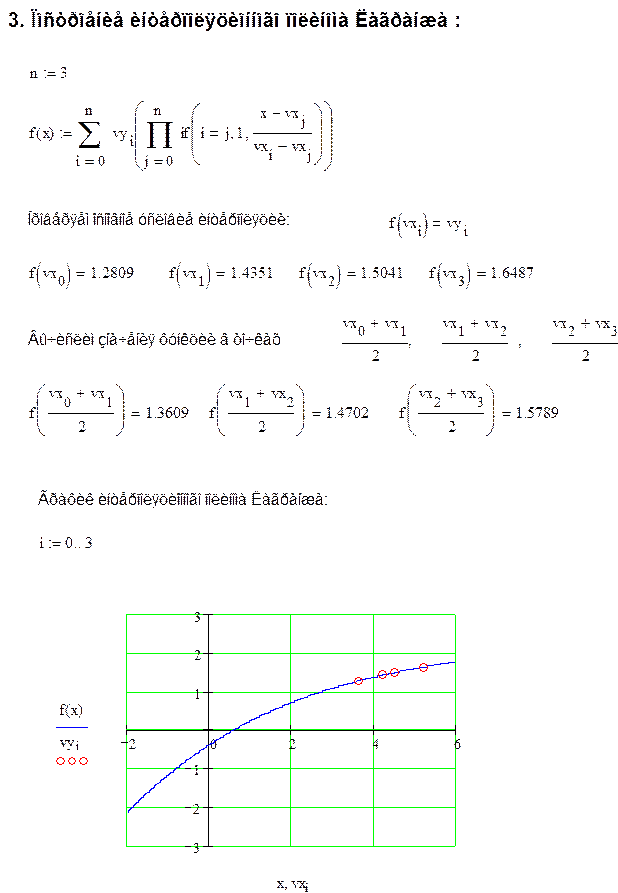
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.