Численные методы: Требования к выполнению лабораторных работ

ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНИХ РАБОТ

При выполнении лабораторных работ студенту необходимо изучить теоретические сведения, записать основные положения и формулы, если требуется, привести геометрическую интерпретацию численного метода. Затем студент должен выполнить ручной счет согласно требованиям и решить предлагаемую задачу с заданной точностью алгоритмически, используя математические пакеты MATLAB и MATHCAD. Для проверки правильности полученных результатов нужно решить поставленную задачу с помощью соответствующих встроенных функций пакетов MATLAB и MATHCAD.

Выполнение лабораторной работы заканчивается выводами, в которых помимо прочего должны быть отмечены преимущества и недостатки изученного численного метода.

Теоретические сведения и выводы должны быть написаны от руки.

Лабораторные работы в пособии разбиты по темам. Теоретическое обоснование методов приведено лишь в той мере, в которой оно необходимо для лучшего усвоения и практического применения. Каждая лабораторная работа содержит примеры выполнения, но не полностью, а лишь те пункты, которые обычно вызывают наибольшие затруднения. Студент должен самостоятельно разобраться с приведенными примерами и программами, дополнить их и, возможно, попытаться улучшить. Это позволит получить более глубокое представление об идеях, лежащих в основе численных методов. Каждая тема заканчивается разделом, в котором рассмотрены возможности инструментальных пакетов MATLAB и MATHCAD для решения соответствующих задач численного анализа.

ТЕМА 1. АППРОКСИМАЦИЯ ФУНКЦИЙ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ (МНК)

Лабораторная работа № 1

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ В СЛУЧАЕ АППРОКСИМАЦИИ ПОЛИНОМАМИ

Цель работы: научиться аппроксимировать таблично заданные функции методом наименьших квадратов.

Постановка задачи

1.  Изучить теоретические сведения.

2.  Провести ручной счёт построения аппроксимирующего многочлена первой степени для таблично заданной функции.

Используя пакеты MathCad и MatLab:

3.  Написать подпрограммы построения аппроксимирующего многочлена для таблично заданной функции.

4.  Определить невязки аппроксимации.

5.  Используя подпрограммы, найти многочлены первой и второй степеней, аппроксимирующие заданную табличную функцию. Определить невязки.

6.  Проверить вычисления с помощью встроенных функций.

7.  Построить графики аппроксимирующих полиномов и заданной функции.

Содержание отчета

1.  Постановка задачи.

2.  Теоретические сведения.

3.  Ручной счет (построение полинома второй степени).

4.  Результаты расчета на ЭВМ.

5.  Выводы.

Теоретические сведения

Аппроксимация – это приближённое выражение известных математических зависимостей объектов через другие, более простые, и, следовательно, более известные.

МНК применяется:

1) При  построении эмпирических формул (получение путём эксперимента). Аналитическое построение  дискретной зависимости между x и y.

2) Аппроксимация функции (приближение);

3) Обработка статистического материала (выделение сигнала на фоне помех).

Для использования МНК должна быть известна либо табличная зависимость x_k, y_k, либо функция, вид которой мы хотим упростить.

Описание метода.Пусть в результате эксперимента получена табл.1 значений функции y(x):

Таблица 1

Требуется аппроксимировать эту функцию многочленом степени  ():

.

Задача метода: подобрать значения параметра a_n= (, , ,…, ) таким образом, чтобы функция

 

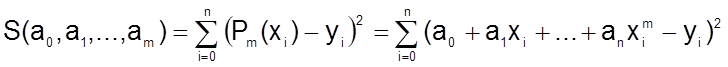
была минимальной.

С учетом необходимых условий существования экстремума функции нескольких переменных получаем систему уравнений для определения неизвестных , , , …, :

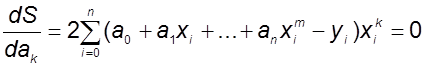              ,  ,    (1)

Доказано, что система (1) имеет единственное решение, при котором  принимает минимальное значение.

Рассмотрим частные случаи:

1)   Пусть , т.е. функцию аппроксимируем многочленом первой степени:

.

Система уравнений для вычисления параметров ,  имеет вид:

;

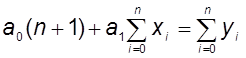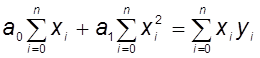                                       .                           (2)

Решив систему, можем записать требуемый многочлен .

2)   Пусть , т.е. функцию аппроксимируем многочленом второй степени:

.

Система уравнений для определения параметров , ,  имеет следующий вид:

;

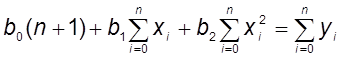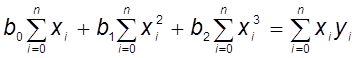                               ;                   (3)

.

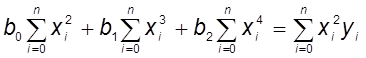Решив систему, можем записать многочлен . Вычисления коэффициентов систем (2) и (3) запишем в виде табл. 2:

Таблица 2

0
1
...	...	...	...	...	...	...	...

Преимущество МНК. При построении аппроксимирующего многочлена по МНК используются все точки таблицы. Если исходные данные получены с некоторыми погрешностями, то МНК сглаживает их.

Примеры выполнения заданий

Функция y(x) задана таблично:

Реализация метода в пакете MATHCAD

1.    Подпрограмма для построения аппроксимирующего многочлена: