results{2} = 'сплайна,заканчивающегося парабалой';
results{3} = strcat(num2str(Splain2(x,y)));
case 5
prompt = {'значение аргумента','значение функции'...
'значения второй производной'};
dlg_title = 'Splain';
num_lines = 1;
def = {'0 1 2 3','0 0.5 2 1.5','-0.3 3.3'};
answer = inputdlg(prompt,dlg_title,num_lines,def);
x = str2num(answer{1});
y = str2num(answer{2});
Deriv2 = str2num(answer{3});
results{1} = 'Матрица коэффициентов';
results{2} = 'сплайна, с заданной кривизной';
results{3} = strcat(num2str(Splain4(x,y,Deriv2)));
case 6
prompt = {'значение аргумента','значение функции'};
dlg_title = 'Splain';
num_lines = 1;
def = {'0 1 2 3','0 0.5 2 1.5'};
answer = inputdlg(prompt,dlg_title,num_lines,def);
x = str2num(answer{1});
y = str2num(answer{2});
results{1} = 'Значения функции';
results{2} = strcat(num2str(VsSplain(x,y)));
case 7
prompt = {'значение аргумента','значение функции'...
'значение производной','значения второй производной'};
dlg_title = 'Splain';
num_lines = 1;
def = {'0 1 2 3','0 0.5 2 1.5','0.2 -1','-0.3 3.3'};
answer = inputdlg(prompt,dlg_title,num_lines,def);
x = str2num(answer{1});
y = str2num(answer{2});
Deriv = str2num(answer{3});
Deriv2 = str2num(answer{4});
results{1} = 'Значение аргумента';
results{2} = strcat(num2str(VseSplain(x,y,Deriv,Deriv2)));
end
helpdlg(results, 'Results');
end
На основании описанного алгоритма в среде Matlab был разработан программный продукт script. Использование данного продукта позволяет строить кубические сплайны с разыми граничными условиями, так же с помощью встроенных функций. В качестве примера была использована функция, заданная таблично (4 точки), с известными значениями первой и второй производной в крайних точках. Исходными данными для работы программы является 4 известных значения аргументов функции, а так же значения в этих точках самой функции. В зависимости от граничных условий, значения первой и второй производных в крайних точках.
Для начала пользователю необходимо вызывать в главном окне функцию script. После запуска появляется окно пользовательского интерфейса (рис. 5.1). Интерфейс программы построен в стиле однооконного приложения. Главное окно состоит из панели с кнопками, выполняющие расчеты.
Рассмотрим назначения каждого оконного элемента:
1- кнопка для построения смыкающегося сплайна.
2- кнопка для построения естественного сплайна.
3- кнопка для построения экстраполяционного сплайна.
4- кнопка для построения сплайна заканчивающегося параболой.
5- кнопка для построения сплайна с заданной кривизной в крайних точках.
6- кнопка для построения сплайна, с помощью встроенной функции.
7- кнопка для построения графиков сплайнов с разными граничными условиями.
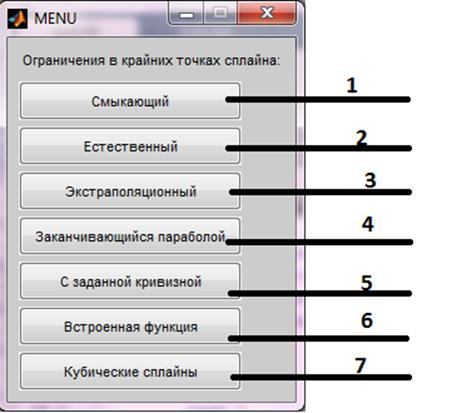
Рисунок 5.1 – стартовое окно программы
При нажатии на кнопки 2, 3, 4, 6 – появиться окно для ввода исходных данных (рис. 5.2). Объясним значения оконных элементов:
1 – область для ввода значений аргумента.
2 – область для ввода значений функции.
3 – кнопка выхода из программы.
4 – кнопка построения кубического сплайна.
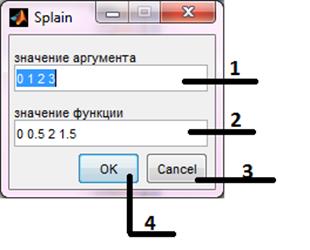
Рисунок 5.2 – Ввод исходных данных
При нажатии на кнопки 1, 5, 7 – появиться окно для ввода исходных данных (рис. 5.3). Объясним значения оконных элементов:
1 – область для ввода значений аргумента.
2 – область для ввода значений функции.
3 – область для ввода значений первой производной в крайних точках.
4 – область для ввода значений второй производной в крайних точках.
5 – кнопка выхода из программы.
6 – кнопка построения кубического сплайна.
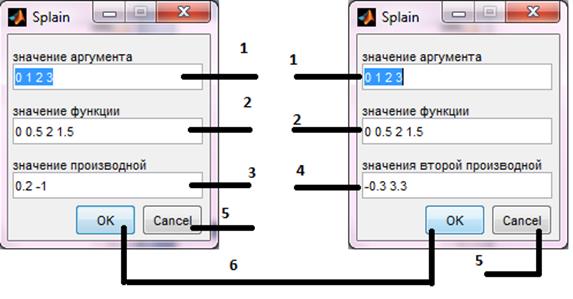
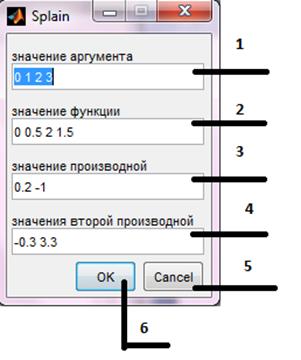
Рисунок 5.3 – Ввод исходных данных.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.