|
|
|
|
|
|
Решив систему методом прогонки, получим следующие результаты:
|
|
|
|
Программный
блок осуществляет посторенние столбца ![]() , с учетом граничных условий
(сплайн заканчивающийся параболой):
, с учетом граничных условий
(сплайн заканчивающийся параболой):
|
|
|
|
|
|
Построение кубического сплайна:
|
|
|
|
Построение графика кубического сплайна:
|
|
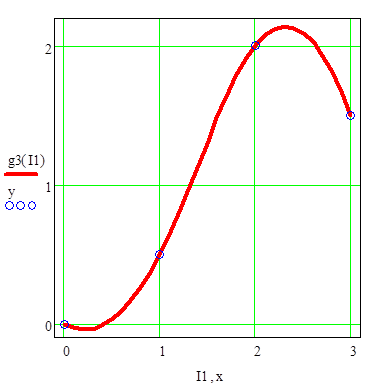
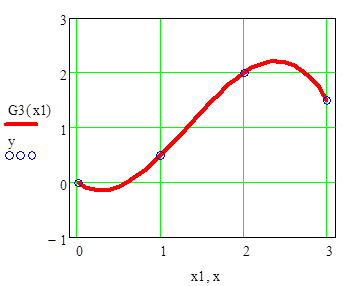
Рисунок 3.4 –График сплайна заканчивающегося параболой
Программный блок, выполняющий посторенние матрицы коэффициентов системы уравнений, с учетом граничных условий (сплайн с заданной кривизной):
|
|
|
|
|
|
Решив систему методом прогонки, получим следующие результаты:
|
|
|
|
Программный
блок осуществляет посторенние столбца ![]() , с учетом граничных условий
(сплайн с заданной кривизной):
, с учетом граничных условий
(сплайн с заданной кривизной):
|
|
|
|
|
|
Построение кубического сплайна:
|
|
|
|
Построение графика кубического сплайна:
|
|
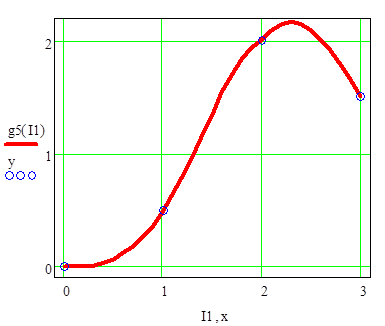
Рисунок 3.5 – График сплайна с заданной кривизной
Построение графиков сплайнов, с помощью встроенных функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
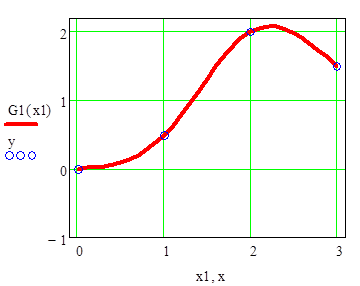
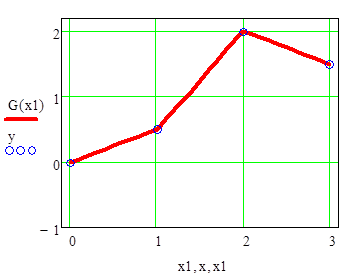
Рисунок 3.6 –Графики кубических сплайнов построенных с помощью встроенных функций
|
|
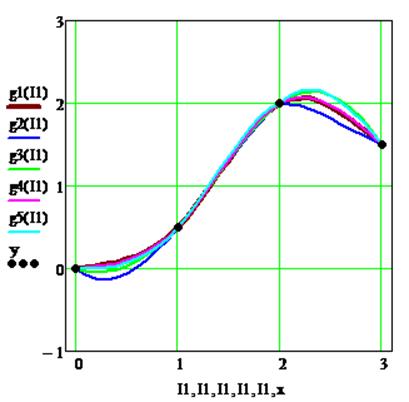
 Рисунок
3.7 – Графики кубических сплайнов, построенных с помощью встроенных функций
Рисунок
3.7 – Графики кубических сплайнов, построенных с помощью встроенных функций
Графики кубических сплайнов, с разными граничными условиями:
|
|
Функции, выполняющие построение матрицы коэффициентов системы уравнений, с учетом граничных условий:
Смыкающийся сплайн:
function A=koefSplain(h, u, d, Deriv, n)
if n>=5
for i= 2:n-3
A(i,i-1)=h(i);
A(i,i)=2*(h(i)+(h(i+1)));
A(i,i+1)=h(i+1);
A(i,n-1)=u(i);
end;
end;
A(1,1)=1.5*h(1)+2*h(2);
A(1,2)=h(2);
A(n-2,n-2)=2*h(n-2)+1.5*h(n-1);
A(n-2,n-3)=h(n-2);
A(1,n-1)=u(1)-3*(d(1)-Deriv(1));
A(n-2,n-1)=u(n-2)-3*(Deriv(2)-d(n-1));
end
Естественный сплайн:
function A=koefSplain3(h, u, d, n)
if n>=5
for i= 2:n-3
A(i,i-1)=h(i);
A(i,i)=2*(h(i)+(h(i+1)));
A(i,i+1)=h(i+1);
A(i,n-1)=u(i);
end;
end;
A(1,1)=2*(h(1)+h(2));
A(1,2)=h(2);
A(n-2,n-2)=2*(h(n-2)+h(n-1));
A(n-2,n-3)=h(n-2);
A(1,n-1)=u(1);
A(n-2,n-1)=u(n-2);
end
Екстраполяционный сплайн:
function A=koefSplain1(h, u, d, n)
if n>=5
for i= 2:n-3
A(i,i-1)=h(i);
A(i,i)=2*(h(i)+(h(i+1)));
A(i,i+1)=h(i+1);
A(i,n-1)=u(i);
end;
end;
A(1,1)=3*h(1)+2*h(2)+h(1)^2/h(2);
A(1,2)=h(2)-h(1)^2/h(2);
A(n-2,n-2)=2*h(n-2)+3*h(n-1)+h(n-1)^2/h(n-2);
A(n-2,n-3)=h(n-2)-h(n-1)^2/h(n-2);
A(1,n-1)=u(1);
A(n-2,n-1)=u(n-2);
end
Сплайн заканчивающийся параболой:
function A=koefSplain2(h, u, d, n)
if n>=5
for i= 2:n-3
A(i,i-1)=h(i);
A(i,i)=2*(h(i)+(h(i+1)));
A(i,i+1)=h(i+1);
A(i,n-1)=u(i);
end;
end;
A(1,1)=3*h(1)+2*h(2);
A(1,2)=h(2);
A(n-2,n-2)=2*h(n-2)+3*h(n-1);
A(n-2,n-3)=h(n-2);
A(1,n-1)=u(1);
A(n-2,n-1)=u(n-2);
end
Сплайн с заданной кривизной в крайних точках:
function A=koefSplain4(h, u, d, Deriv2, n)
if n>=5
for i= 2:n-3
A(i,i-1)=h(i);
A(i,i)=2*(h(i)+(h(i+1)));
A(i,i+1)=h(i+1);
A(i,n-1)=u(i);
end;
end;
A(1,1)=2*(h(1)+h(2));
A(1,2)=h(2);
A(n-2,n-2)=2*(h(n-2)+h(n-1));
A(n-2,n-3)=h(n-2);
A(1,n-1)=u(1)-h(1)*Deriv2(1);
A(n-2,n-1)=u(n-2)-Deriv2(2);
end
Функция решает построенную систему методом прогонки:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.