Изучение численного метода интерполяции кубическими сплайнами с различными видами граничных условий, страница 4

Лемма 1.3. Экстраполяционный сплайн. Существует единственный кубический сплайн, который используется для экстраполирования по внутренним узлам  и , чтобы найти , и экстраполирования по узлам  и ,  чтобы найти .

Доказательство. Решим линейную систему

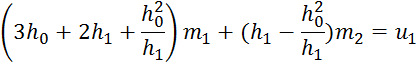
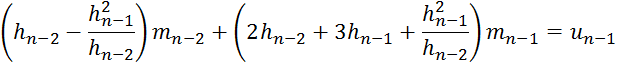
Замечание. Экстраполяционный сплайн эквивалентен предположению, что край кубического полинома является продолжением смежного кубического полинома, т. е. форма сплайна —единственная кубическая кривая на интервале [; ] и другая единственная кубическая кривая на интервале [; ]

Лемма 1.4. Сплайн заканчивающийся параболой. Существует такой единственный кубический сплайн, что  на интервале [; ] и  на интервале [; ].

Доказательство. Решим линейную систему

.

Замечание. Предположение, что   на интервале [; ], заставляет кубическую кривую вырождаться в параболу на интервале [; ] и подобная ситуация происходит на интервале [; ].

Лемма 1.5. Сплайн с заданной кривизной в крайних точках. Существует единственный кубический сплайн с заданными значениями второй производной в крайних точках .

Доказательство. Решим линейную систему

.

Замечание. Задавая значения , профессионал имеет возможность получать нужную кривизну в каждой крайней точке [3].

3 РЕАЛИЗАЦИЯ ВЫЧИСЛЕНИЙ С ПОМОЩЬЮ ПРОГРАММНОГО ПАКЕТА MATHCAD

Ввод исходных данных:

Программный блок, выполняющий посторенние матрицы коэффициентов системы уравнений, с учетом граничных условий(смыкающийся сплайн):

Программный блок, решает построенную систему методом прогонки:

          Программный блок осуществляет посторенние столбца , с учетом граничных условий (смыкающийся сплайн)

Построение кубического сплайна:

Построение графика кубического сплайна:

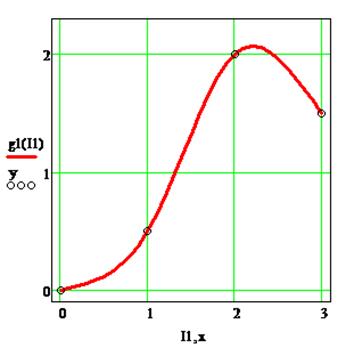
Рисунок 3.1 – График смыкающегося сплайна

Программный блок, выполняющий посторенние матрицы коэффициентов системы уравнений, с учетом граничных условий(естественный сплайн):

          Решив систему методом прогонки, получим следующие результаты:

Программный блок осуществляет посторенние столбца , с учетом граничных условий (естественный сплайн):

Построение кубического сплайна:

Построение графика кубического сплайна:

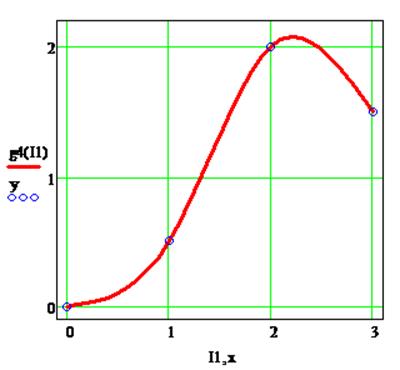
Рисунок 3.2 – График естественного сплайна

Программный блок, выполняющий посторенние матрицы коэффициентов системы уравнений, с учетом граничных условий (экстраполяционный сплайн):

          Решив систему методом прогонки, получим следующие результаты:

          Программный блок осуществляет посторенние столбца , с учетом граничных условий (экстраполяционный сплайн):

Построение кубического сплайна:

Построение графика кубического сплайна:

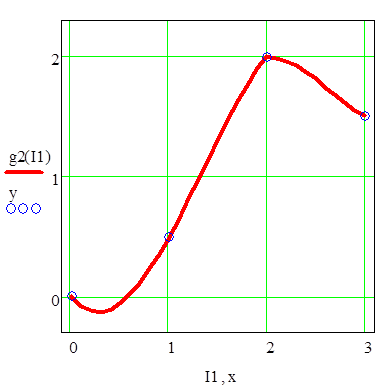
Рисунок 3.3 – График экстраполяционного сплайна

Программный блок, выполняющий посторенние матрицы коэффициентов системы уравнений, с учетом граничных условий (сплайн заканчивающийся параболой):