Символ суммы. Детерминанты: определение и свойства. Вычисление детерминантов. Правило Крамера. Метод Гаусса решения системы

ЛЕКЦИЯ № 1

1.  Символ 

В математике часто приходится рассматривать сумму большого числа слагаемых. Для таких сумм введено следующее обозначение:

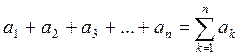
Индекс  называется индексом суммирования. В качестве индекса суммирования может быть употреблена и любая другая буква.

Имеют место следующие правила обращения со знаком суммы ,

1.  Обозначение индекса суммирования может быть изменено                             

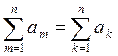
2.  Множитель,  не  зависящий  от  индекса  суммирования, может быть вынесен за знак суммы:

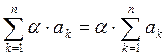
3.  Два знака суммы могут быть переставлены

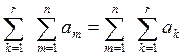
Доказательство приведенных правил легко доказывается на основании введенного символа суммирования. Для примера доказательства докажем правило 2.

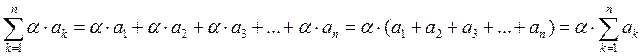
Что и требовалось доказать.

2.  Детерминанты. Определение и свойства

Определение. Матрицей размеров  называется совокупность  чисел, расположенных в виде таблицы из  строк и  столбцов:

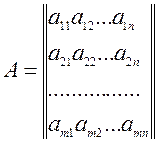
Числа , составляющие матрицу, называются элементы матрицы и обозначаются буквами с двумя индексами, первый из них обо­значает номер строки, а второй – номер  столбца. Если число строк в матрице равно числу столбцов, то матрица называется квадратной. Если же число строк в матрице неравно числу столбцов, то матрица называется  прямоугольной.

Детерминантом (определителем) матрицы  мы будем обозначать  или,

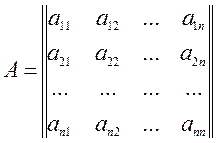
Определение. Детерминант квадратной матрицы – это число, которое ставится в соответствие матрице и может быть вычислено по ее элементам по формуле.

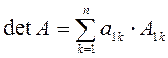
 - элементы  матрицы

- алгебраическое дополнение соответствующего элемента матрицы, которое вычисляется по формуле

где - минор соответствующего элемента матрицы.   

Определение. Минор это детерминант матрицы порядка , полученной из  вычеркиванием  строки и -го столбца.

Определение. Матрица порядка 1 состоит из одного числа, и ее детерминант по определению считают равным этому числу.

На первый взгляд это определение может показаться не эффективным: детерминант матрицы порядка определяется через детерминанты матрицы порядка , а эти детерминанты сами не определены. В действительности же в этом ничего, плохого нет. Для определения чисел мы можем воспользоваться той же формулой, поскольку она имеет место для матриц любого порядка. Тем самым мы выразим через детерминанты матриц порядка . Можно продолжать этот процесс, пока мы не придем к матрицам первого порядка, а для них детерминант определен непосредственно.

Применим наше определение к матрицам 2 – го  порядка.

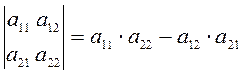
Единичной матрицей называется матрица.

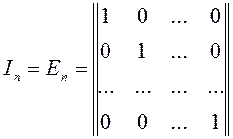
Для нее , так как, раскрывая определитель по определению, мы получаем  и так далее. И окончательно .

Определение. Если в матрице  поменять местами строки и столбцы, то полученная матрица будет называться транспонированной, а переход от к  - транспонирование.

Матрицу, полученную из матрицы  транспонированием, обозначают .

Сформулируем одну очень важную теорему в теории определителей.

Теорема. Для каждой квадратной матрицы порядка  имеет место формула

 

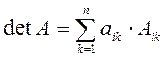
или                                         

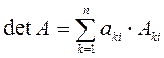
Эти формулы называются формулами разложения детерминанта соответственно по строке и по столбцу.

Доказательство: Доказательство мы проведем методом полной индукции. Начнем с первой формулы. Непосредственно очевидно, что для матриц второго порядка она справедлива 

Допустим, что формула верна для матриц порядка , и докажем ее для матрицы порядка.

При любом  минор  рассматриваемой матрицы есть детерминант некоторой матрицы порядка , в которую входит (без своего элемента) -я строка матрицы . Пользуясь предположением индукции, мы можем разложить по этой строке.

 

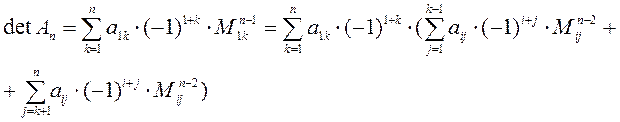
Минор  получен из матрицы вычеркиванием 1-й и -й строк и -го и -го столбцов, таким образом у нас . И мы получим, поменяв порядок суммирования

      

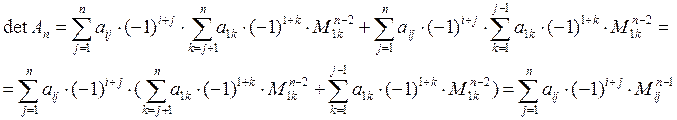
Что и требовалось доказать.

Доказательство второй формулы теоремы совершенно аналогично проведенному доказательству и провести его, мы предоставляем читателю.

Свойства детерминантов.

Свойство 1. Для любой квадратной матрицы

Доказательство: Доказательство мы проведем методом полной индукции. Начнем с первой формулы. Непосредственно очевидно, что для матриц второго порядка она справедлива 

Допустим, что формула верна для матриц порядка , и докажем ее для матрицы порядка.

Пусть матрица, получаемая из вычеркиванием -й строки и -го столбца, а матрица , получаемая из вычеркиванием -й строки и -го столбца. Легко видеть, что, . Поэтому из предложения индукции следует, что  , или, словами, дополнительный минор элемента в матрице равен дополнительному минору элемента в матрице . Кроме того, , и разложение  по -й строке совпадает с разложением по -му столбцу. Свойство доказано.