Символ суммы. Детерминанты: определение и свойства. Вычисление детерминантов. Правило Крамера. Метод Гаусса решения системы, страница 2

Из свойства 1 следует равноправность строк и столбцов. Именно, если справедливо какое-либо утверждение о детерминантах, касающееся строк соответствующих матриц, то верно и аналогичное утверждение, касающееся столбцов, и обратно.

Свойство 2. Если элементы одной строки или столбца детерминанта равны нулю, то и детерминант равен нулю.

Доказательство: Доказательство вытекает из доказанной ранее теоремы. Раскроим детерминант по   -й строке

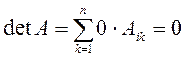
что и требовалось доказать.

Свойство 3. Для того чтобы умножить детерминант на число, достаточно умножить на это число строку (столбец).

Доказательство: Доказательство вытекает из доказанной ранее теоремы. Раскроим детерминант по   -й строке

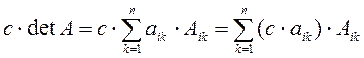
Таким образом каждый элемент -й строки умножился на , что и требовалось доказать.

Свойство 4. Если одна из строк (столбцов) является суммой двух строк (столбцов), то её детерминант есть сумма детерминантов соответствующих матриц.

Доказательство: Доказательство вытекает из доказанной ранее теоремы. Раскроим детерминант по   -й строке

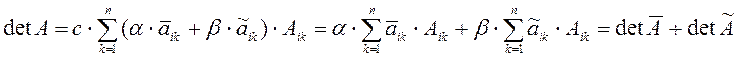
что и требовалось доказать.

Свойство 5. Если в матрице поменять местами какие-нибудь две строки (столбца), то ее детерминант изменит знак.

Доказательство: Доказательство мы проведем методом полной индукции. Непосредственно очевидно, что для матриц второго порядка она справедлива 

Здесь  матрица, у которой поменяли местами строки.

Допустим, что формула верна для матриц порядка , и докажем ее для матрицы порядка . Детерминант матрицы порядка мы разложим по любому столбцу, отличному от переставляемых столбцов. Переставляемые столбцы входят в каждый дополнительный минор, и если предложение справедливо для матриц порядка , при перестановке столбцов каждый минор меняет знак. Отсюда вытекает, что знак изменится и у детерминанта, что и заканчивает доказательство.

В качестве следствий из свойства 4 мы получим следующие свойство.

Свойство 6.  Если в матрице есть два две одинаковые строки (одинаковых столбца), то .

Доказательство: Действительно, при перестановке одинаковых столбцов мы не изменяем матрицу, а изменим знак у детерминанта. Отсюда  и, следовательно, , что и требовалось доказать.

Свойство 7. Справедливы следующие формулы

,      

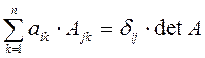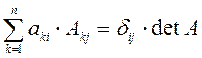
Здесь  - символ Кронекера, который определён следующим образом

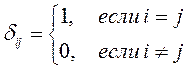
Доказательство: Если то мы получаем детерминант, раскрытый по -ой строке. Если же то получается детерминант, у которого две строки равные, а он по 5 свойству детерминантов равен нулю, что и требовалось доказать.

Свойство 8. Детерминант матрицы не изменится, если к какой-нибудь строке (какому – нибудь  ее столбцу) прибавить линейную комбинацию остальных строк (столбцов) этой матрицы.

Доказательство: К -й строке прибавим линейную комбинацию остальных строк, а затем раскроем определитель по -й строке.

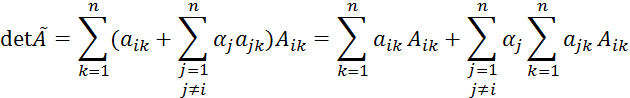
  По свойству 7 .

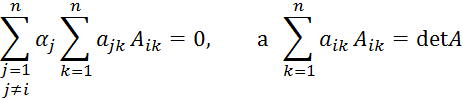
Тогда получаем   свойство доказано.

3.  Вычисление детерминантов.

Используя свойства детерминантов, его можно привести к диагональному виду

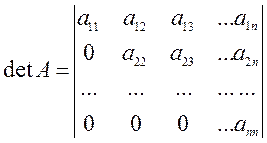
Полученный детерминант вычисляется по формуле .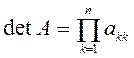

Метод сведение детерминанта к диагональному виду называется методом последовательных исключений, который впервые предложил Гаусс.

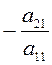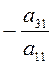Опишем его. Пусть , это предположение не ограничивает общность рассуждений, в силу свойств детерминантов (если , то поменяем местами столбцы, поменяв знак на противоположный ). Умножим первую строку на  и сложим со второй строкой, тогда на первом месте во второй строке будет ноль. Умножим первую строку на  и сложим с третей строкой, тогда на первом месте в третей строке будет ноль и так далее. Мы получим детерминант

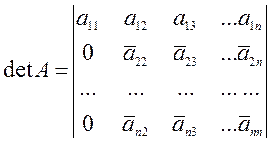
в котором 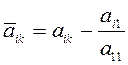. Аналогичным образом сделаем нули во втором столбце под элементом  и так далее. Если в процессе вычислений в одной из строк все элементы получатся равные нулю, то и детерминант будет равен нулю.

4. Системы линейных уравнений

Систему уравнений вида

    

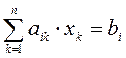
мы будем называть системой  линейных уравнений с  неизвестными . Коэффициенты этих урав­нений мы будем записывать в виде матрицы

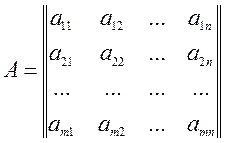
называемой матрицей системы. Числа, стоящие в пра­вых частях уравнений, образуют столбец , называемый столбцом свободных членов.

Определение. Совокупность  чисел  называется решением системы, если каждое уравне­ние системы обращается в тождество после подстановки в него чисел  вместо соответствующих неизвестных .