Задача состоит в нахождении решений системы, причем мы не делаем заранее никаких предположений относительно коэффициентов и свободных членов системы и даже относительно числа уравнений и числа неизвестных. Поэтому могут представиться различные возможности. Система может вообще не иметь решения.
Системы, не имеющие решений, мы будем называть несовместными, а имеющие решения — совместными.
5. Правило Крамера.
Рассмотрим
случай, когда число уравнений равно числу неизвестных, ![]() . Кроме того, мы наложим определенные
условия на коэффициенты системы. Если этого не сделать, нам придется изучать
здесь, например, и систему, состоящую из одного уравнения, повторенного
. Кроме того, мы наложим определенные
условия на коэффициенты системы. Если этого не сделать, нам придется изучать
здесь, например, и систему, состоящую из одного уравнения, повторенного ![]() раз. Мы хотим, чтобы все уравнения
системы были в определенном смысле независимы. Уже в школьном курсе широко
применялся следующий прием: умножали первое уравнение на число а, второе
уравнение —на число р, а затем складывали эти уравнения почленно. Полученное
уравнение (его естественно назвать линейной комбинацией исходных уравнений)
является их следствием. Мы хотим, чтобы в нашей системе ни одно уравнение не
являлось линейной комбинацией остальных. Если это выполнено, мы будем говорить,
что уравнения
раз. Мы хотим, чтобы все уравнения
системы были в определенном смысле независимы. Уже в школьном курсе широко
применялся следующий прием: умножали первое уравнение на число а, второе
уравнение —на число р, а затем складывали эти уравнения почленно. Полученное
уравнение (его естественно назвать линейной комбинацией исходных уравнений)
является их следствием. Мы хотим, чтобы в нашей системе ни одно уравнение не
являлось линейной комбинацией остальных. Если это выполнено, мы будем говорить,
что уравнения
линейно независимы.
В
случае ![]() для линейной независимости уравнений
системы достаточно потребовать, чтобы детерминант матрицы системы был отличен
от нуля. (Поскольку
для линейной независимости уравнений
системы достаточно потребовать, чтобы детерминант матрицы системы был отличен
от нуля. (Поскольку ![]() , и матрица квадратная, имеет
смысл говорить об ее детерминанте.) Действительно, заметим, что при умножении
какого-нибудь уравнения на число соответствующая сложении уравнений строки
матрицы складываются. Поэтому, если одно из уравнений является линейной комбинацией
остальных, соответствующая строка матрицы системы есть линейная комбинация
остальных строк. Из предложения следует, что при этом детерминант матрицы
системы равен нулю.
, и матрица квадратная, имеет
смысл говорить об ее детерминанте.) Действительно, заметим, что при умножении
какого-нибудь уравнения на число соответствующая сложении уравнений строки
матрицы складываются. Поэтому, если одно из уравнений является линейной комбинацией
остальных, соответствующая строка матрицы системы есть линейная комбинация
остальных строк. Из предложения следует, что при этом детерминант матрицы
системы равен нулю.
Теорема (правило Крамера). Система из ![]() уравнений с
уравнений с ![]() неизвестными
неизвестными
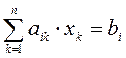
в случае, когда детерминант матрицы системы отличен от нуля, имеет решение и притом только одно. Это решение находится по формулам
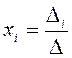
![]()
где через ![]() обозначен
детерминант матрицы системы, а через
обозначен
детерминант матрицы системы, а через ![]() — детерминант
матрицы, получаемой из матрицы системы заменой
— детерминант
матрицы, получаемой из матрицы системы заменой ![]() -го
столбца столбцом свободных членов.
-го
столбца столбцом свободных членов.
Доказательство. Докажем сначала, что
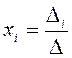
![]()
представляет собой решение системы.
Подставим эти решения в левую часть системы
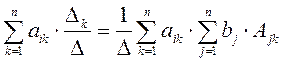
Поменяем порядок суммирования
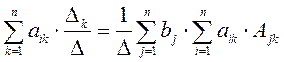
Известно,
что 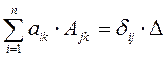
тогда, получаем
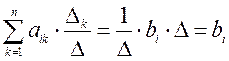
Что и требовалось доказать.
Докажем теперь, что решение системы единственно, т. е. каждое решение системы должно совпадать с решением Крамера.
Домножим обе части системы на
![]() и просуммируем по
и просуммируем по ![]() .Здесь
.Здесь
![]() - алгебраическое дополнение
элемента
- алгебраическое дополнение
элемента ![]() матрицы системы. После перемены порядка
суммирования, получаем
матрицы системы. После перемены порядка
суммирования, получаем
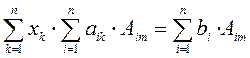
По
свойствам определителей 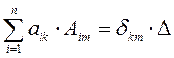 , а
, а 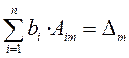 (детерминант матрицы, получаемой из
матрицы системы заменой
(детерминант матрицы, получаемой из
матрицы системы заменой ![]() -го столбца столбцом свободных
членов)и тогда приходим к уравнению
-го столбца столбцом свободных
членов)и тогда приходим к уравнению
![]()
Если
![]() , то мы получаем формулу Крамера
, то мы получаем формулу Крамера
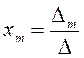
![]()
Единственность решения
доказана, так как номер ![]() был взят произвольно.
был взят произвольно.
В
случае, когда ![]() необходимо проводить
дополнительные исследования системы.
необходимо проводить
дополнительные исследования системы.
Пример. Решить систему линейных алгебраических уравнений методом Крамера.
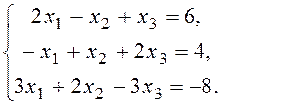
Решение: По правилу Крамера решение системы линейных алгебраических уравнений, если главный определитель системы отличен от нуля, запишется
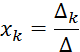
Здесь ![]() – главный определитель системы,
– главный определитель системы,
![]() – детерминант матрицы, получаемой из матрицы
системы заменой
– детерминант матрицы, получаемой из матрицы
системы заменой ![]() -го столбца столбцом свободных
членов
-го столбца столбцом свободных
членов
Вычислим эти определители
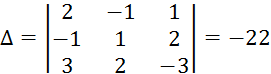
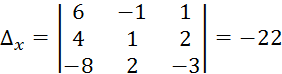
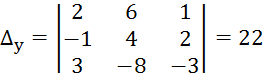
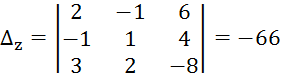
И тогда
![]() ;
; ![]() ; z
; z![]()
И окончательно ![]()
Проведем проверку
![]()
![]()
![]()
Система решена.
6. Метод Гаусса решения системы.
Этот метод решения системы, сродни методу Гаусса нахождения определителя.
Составляется расширенная матрица системы, состоящая из матрицы системы и столбца свободных членов
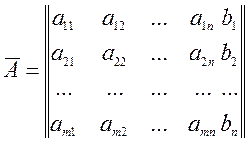
Которая по методу Гаусса сводится к диагональному виду
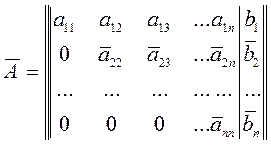
Для определения ![]() мы получили уравнение
мы получили уравнение
![]()
откуда, если ![]() , то
, то 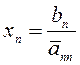
Для определения ![]() мы получили уравнение
мы получили уравнение
![]()
Зная ![]() нетрудно
найти
нетрудно
найти ![]()
Продолжая этот процесс, мы
дойден до ![]() .
.
Пример. Решить систему линейных алгебраических уравнений методом Гаусса.
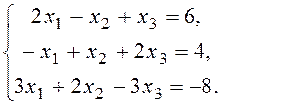
Решение: Составим расширенную матрица системы, состоящую из матрицы системы и столбца свободных членов. Для удобства поменяем местами первые два уравнения.
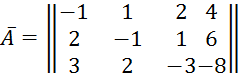
По методу Гаусса сведём матрицу к диагональному виду
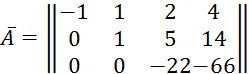
И мы пришли к системе
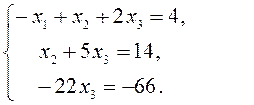
Из полученной системы ![]()
Проведем проверку
![]()
![]()
![]()
Система решена.
Решение полученное методом Крамера и методом Гаусса совпали.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.