Лекция 5.
Евклидовы пространства
Определим операцию скалярного умножения векторов, а длину и угол введем при помощи скалярного произведения.
Определение. Вещественное
линейное пространство называется евклидовым, если в нем определена операция
скалярного умножения: любым двум векторам ![]() сопоставлено вещественное число, удовлетворяющее
следующим условиям:
сопоставлено вещественное число, удовлетворяющее
следующим условиям:
для
любых ![]()
1. ![]()
2. ![]()
3. ![]()
4. ![]() , если
, если ![]()
Введем следующее определение.
Определение. Назовем длиной вектора ![]() и обозначим
число
и обозначим
число![]() . Углом между векторами
. Углом между векторами ![]() назовем число
назовем число ![]() ,
удовлетворяющее условию
,
удовлетворяющее условию
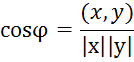
В силу аксиомы 4 длина вектора - вещественное неотрицательное число (мы рассматриваем арифметическое значение корня). Длина вектора равна нулю тогда и только тогда, когда вектор нулевой.
С определением угла дело обстоит несколько сложнее. Нужно доказать, что выражение в правой части равенства по абсолютной величине не превосходит единицы. Это следует из неравенства
![]()
связываемого с именами Шварца, Коши и Буняковского. Докажем это неравенство.
В случае ![]() или
или ![]() соотношение очевидно.
соотношение очевидно.
Пусть ![]() – произвольные векторы в евклидовом
пространстве. При любых
– произвольные векторы в евклидовом
пространстве. При любых ![]() имеет место соотношение
имеет место соотношение
![]()
причем равенство нулю достигается тогда и только
тогда, когда ![]() . Равенство имеет место тогда и
только тогда, когда
. Равенство имеет место тогда и
только тогда, когда ![]() линейно зависимы.
линейно зависимы.
Пусть существует нетривиальная линейная комбинация ![]() . Умножая ее последовательно на
. Умножая ее последовательно на ![]() , получим равенства
, получим равенства
![]()
![]()
Детерминант однородной системы, имеющей нетривиальное решение, равен нулю. Отсюда следует нужное равенство.
![]()
Предположим теперь, что ![]() линейно независимы. Положив
линейно независимы. Положив ![]() и
и ![]() мы получим
мы получим
![]()
откуда и вытекает требуемое неравенство, если ![]() .
.
Из доказанного неравенства следует еще одно простое и полезное неравенство, а именно
![]()
Оно вытекает из следующей цепочки соотношений:
![]()
Знак
равенства имеет место, если ![]() , т. е. если угол между
, т. е. если угол между ![]() равен нулю, и только в этом случае. Полученное
неравенство называется неравенством треугольника, так как, если векторы
являются направленными отрезками, оно означает, что сторона треугольника меньше
суммы двух других его сторон.
равен нулю, и только в этом случае. Полученное
неравенство называется неравенством треугольника, так как, если векторы
являются направленными отрезками, оно означает, что сторона треугольника меньше
суммы двух других его сторон.
Определение. Ненулевые векторы
![]() называются перпендикулярными или ортогональными,
если
называются перпендикулярными или ортогональными,
если ![]() .
.
Нулевой вектор мы по определению будем считать ортогональным любому вектору.
Утверждение 1. Только нулевой вектор ортогонален каждому вектору.
Доказательство:
Действительно, если ![]() для всех
для всех ![]() , то, положив
, то, положив ![]() , имеем
, имеем ![]() , что возможно только для нулевого вектора.
, что возможно только для нулевого вектора.
Систему
векторов ![]() в евклидовом пространстве мы назовем ортонормированной, если
в евклидовом пространстве мы назовем ортонормированной, если ![]() при
при ![]() и
и ![]() каковы бы ни были номера
каковы бы ни были номера ![]()
Утверждение 2. Ортонормированная система векторов линейно независима.
Доказательство:
Пусть ![]() ортонормированная система векторов. Рассмотрим
равенство
ортонормированная система векторов. Рассмотрим
равенство ![]() . Умножая скалярно это равенство на
. Умножая скалярно это равенство на ![]() , получаем
, получаем
![]()
Так
как ![]() при
при![]() и
и ![]() , то из этого вытекает, что
, то из этого вытекает, что ![]() при произвольном
при произвольном ![]() . Таким образом,
каждая равная нулю линейная комбинация векторов
. Таким образом,
каждая равная нулю линейная комбинация векторов ![]() необходимо тривиальная. Утверждение доказано.
необходимо тривиальная. Утверждение доказано.
Далее мы будем предполагать, что евклидово пространство имеет конечную размерность п.
Теорема. В n-мерном евклидовом пространстве существует ортонормированная система из п векторов.
Доказательство: Заметим, что в силу утверждения 2 такая система векторов является базисом. Мы будем называть этот базис ортонормированным.
Возьмем
в n-мерном
евклидовом пространстве базис ![]() и проведем ортогонализацию этого базиса.
и проведем ортогонализацию этого базиса.
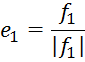
Построим
вектора ![]() так, чтобы он был ортогональны векторам
так, чтобы он был ортогональны векторам ![]()
![]()
Коэффициенты
![]() , выберем так, чтобы вектор
, выберем так, чтобы вектор ![]() был ортогонален ко всем векторам
был ортогонален ко всем векторам ![]() . Так как система
. Так как система ![]() ортонормированна, мы имеем
ортонормированна, мы имеем ![]() , откуда
, откуда ![]() для всех
для всех ![]() . Пронормирмируем вектора
. Пронормирмируем вектора ![]()
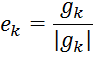
мы
и приходим к базису ![]() .
.
Мы получили систему единичных и ортогональных векторов.
Этот метод называется методом ортогонализации.
Выражение
скалярного произведения через компоненты сомножителей. Пусть в евклидовом
пространстве задан базис ![]() . Это позволяет нам записать любые векторы в этом
базисе
. Это позволяет нам записать любые векторы в этом
базисе
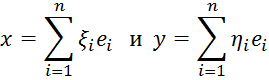
Найдем скалярное произведение
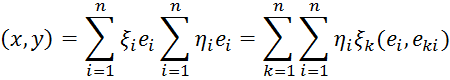
Если
базис ортонормированный, то ![]() при k
при k![]() и
и ![]() и в сумме остаются только те слагаемые, для которых
и в сумме остаются только те слагаемые, для которых
![]() .
.
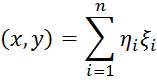
Возьмем в евклидовом пространстве произвольный
базис ![]() . Рассмотрим числа их принято обозначать через
. Рассмотрим числа их принято обозначать через ![]() всевозможные попарные скалярные
произведения базисных векторов. Их принято обозначать
через
всевозможные попарные скалярные
произведения базисных векторов. Их принято обозначать
через ![]() и записывать в виде квадратной матрицы
и записывать в виде квадратной матрицы
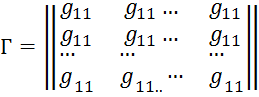
Эта
матрица называется матрицей Грамма базиса ![]() . В
силу коммутативности скалярного умножения
. В
силу коммутативности скалярного умножения ![]() , следовательно,
матрица удовлетворяет условию
, следовательно,
матрица удовлетворяет условию ![]() , т. е. не меняется при
транспонировании. Такие матрицы называются симметрическими.
, т. е. не меняется при
транспонировании. Такие матрицы называются симметрическими.
Мы
обозначим через ![]() координатные столбцы векторов
координатные столбцы векторов ![]() . Тогда, скалярное
произведение можно записать в матричной форме так:
. Тогда, скалярное
произведение можно записать в матричной форме так:
![]()
Базис ортонормирован тогда и только тогда, когда его матрица Грамма - единичная матрица. Поэтому для ортонормированного базиса
![]()
Пусть
нам даны два базиса ![]() и
и
![]() Запишем базис
Запишем базис ![]() через
матрицу
через
матрицу ![]() и
аналогично
и
аналогично ![]() . Они связаны при помощи матрицы
перехода S по формуле e
. Они связаны при помощи матрицы
перехода S по формуле e![]() .
Матрицу Грамма через матрицу
.
Матрицу Грамма через матрицу ![]() можно записать так
можно записать так
![]()
С учетом этого запишем матрицу Грамма в новой системе координат
![]()
И окончательно
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.