Евклидовы пространства. Определение операции скалярного умножения векторов

Лекция 5.

Евклидовы пространства

Определим операцию скалярного умножения векторов, а длину и угол введем при помощи скалярного произведения.

Определение. Вещественное линейное простран­ство называется евклидовым, если в нем определена опе­рация скалярного умножения: любым двум векторам  сопоставлено вещественное число, удовлетворяющее следующим  условиям:

для любых  

1. 

2. 

3. 

4.  , если

Введем следующее определение.

Определение. Назовем длиной вектора и обо­значим число. Углом между векторами назовем число ,   удовлетворяющее   условию

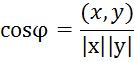
В силу аксиомы 4 длина вектора - вещественное неотрицательное число (мы рассматриваем арифметиче­ское значение корня). Длина вектора равна нулю тогда и только тогда, когда вектор нулевой.

С определением угла дело обстоит несколько слож­нее. Нужно доказать, что выражение в правой части равенства  по абсолютной величине не прево­сходит единицы. Это следует из неравенства

связываемого с именами Шварца, Коши и Буняковского. Докажем это неравенство.

В случае  или  соотношение очевидно.

Пусть – произвольные векторы в евклидовом пространстве. При любых  имеет место соотно­шение

причем равенство нулю достигается тогда и только тогда, когда . Равенство имеет место тогда и только тогда, когда линейно зависимы.

Пусть существует нетривиальная линейная комбинация . Умножая ее последовательно на , полу­чим равенства

Детерминант однородной системы, имеющей нетривиаль­ное решение, равен нулю. Отсюда следует нужное ра­венство.

Предположим теперь, что  линейно независимы. Положив  и  мы получим

откуда и вытекает требуемое неравенство, если .

Из доказанного неравенства  следует еще одно простое и полезное нера­венство, а именно

Оно вытекает из следующей цепочки соотношений:

Знак равенства имеет место, если , т. е. если угол между равен нулю, и только в этом случае. Полученное неравенство называется неравенством треугольника, так как, если векторы являются направленными отрезками, оно означает, что сторона треугольника меньше суммы двух других его сторон.

Определение. Ненулевые векторы называются перпендикулярными или ортогональными, если  .

Нулевой вектор мы по определению будем считать ортогональным любому вектору.

Утверждение 1. Только нулевой вектор ортого­нален каждому вектору.

Доказательство: Действительно, если   для всех , то, поло­жив , имеем , что возможно только для нулевого вектора.

Систему векторов    в евклидовом пространстве мы назовем ортонормированной, если   при    и    каковы бы ни были номера

Утверждение 2. Ортонормированная система векторов линейно независима.

Доказательство:  Пусть  ортонорми­рованная система векторов. Рассмотрим равенство . Умножая скалярно это равенство на   , получаем

Так как  прии , то из этого вытекает, что    при произвольном . Таким образом, каждая равная нулю линейная комбинация векторов  необходимо тривиальная. Утверждение доказано.

Далее мы будем предполагать, что евклидово про­странство имеет конечную размерность п.

Теорема.  В n-мерном евклидовом пространстве существует   ортонормированная   система  из п векторов.

Доказательство: Заметим, что в силу утверждения 2 такая система векторов является базисом. Мы будем называть этот базис ортонормированным.     

Возьмем  в n-мерном евклидовом пространстве базис и проведем ортогонализацию этого базиса.

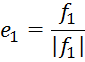
Построим вектора  так, чтобы он был ортогональны векторам  

Коэффициенты ,  выберем так, чтобы век­тор  был ортогонален ко всем векторам . Так   как   система      ортонормированна,  мы имеем  ,   откуда    для всех . Пронормирмируем вектора

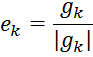
мы и приходим к базису .

Мы получили систему единичных и ортогональных векторов.

Этот метод  назы­вается методом ортогонализации. 

Выражение скалярного произведения через ком­поненты сомножителей. Пусть в евклидовом простран­стве задан базис . Это позволяет нам за­писать любые векторы в этом базисе

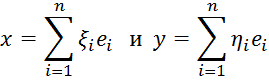
Найдем скалярное произведение

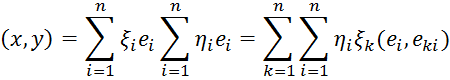
Если   базис  ортонормированный,  то при kи  и   в сумме остаются только те слагаемые, для которых .

Возьмем в евклидовом простран­стве произвольный базис . Рассмотрим числа их принято обозна­чать через  всевозможные попарные скалярные произведения базисных векторов.  Их принято обозна­чать через   и записывать в виде квадратной матрицы

Эта матрица называется матрицей Грамма  базиса . В силу коммутативности скалярного умно­жения , следовательно, матрица удовлетворяет условию  , т. е. не меняется при транспонировании. Такие матрицы называются симметрическими.

Мы обозначим через  координатные столбцы векторов  . Тогда, скалярное произведение можно записать в матрич­ной форме так:

Базис ортонормирован тогда и только тогда, когда его матрица Грамма - единичная матрица. Поэтому для ортонормированного базиса

Пусть нам даны два базиса и   Запишем базис через матрицу и аналогично   . Они связаны при помощи матрицы перехода S по формуле e. Матрицу Грамма через матрицу  можно записать так

С учетом этого запишем матрицу Грамма в новой системе координат

И окончательно