Евклидовы пространства. Определение операции скалярного умножения векторов, страница 2

Мы получили формулу, связывающую матрицу Грамма в разных системах координат.

Рассмотрим полученную формулу в случае, когда базис е ортонормированный. Тогда  .  Вычислим детерминант обеих частей равенства, полу­чим . Поскольку базис  - произвольный, отсюда следует

Утверждение. Детерминант матрицы Грамма  любого базиса положителен.

Действительно, так как преобразование базиса не вырождено, то  и тогда  . Утверждение доказано.

Последнее предложение может быть усилено сле­дующим образом.

Теорема 2. Пусть -  произвольные (не обязательно линейно независимые) векторы в евклидовом пространстве. Тогда детерминант матрицы

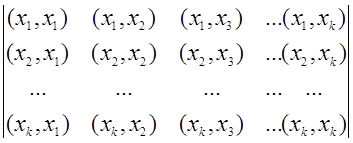
составленной из их попарных скалярных произведений, положителен, если векторы линейно независимы, и равен нулю, если они линейно зависимы.

Первое утверждение теоремы прямо следует из доказанного утверждения, так как если  линейно неза­висимы, они образуют базис.

Докажем второе утверждение. Если векторы линейно зависимы, то выполнено равенство , в котором среди коэффициентов  есть отлич­ные от нуля. Умножая это равенство скалярно на каждый из векторов , мы придем к системе линейных уравнений

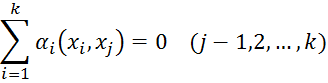
которой удовлетворяют коэффициенты . Так как система имеет нетривиальное решение, детерминант ее матрицы должен равняться нулю, что и требо­валось.

Заметим, что доказанное выше неравенство Коши – Буняковского является частным случаем этой теоремы для k = 2.

Возьмем в евклидовом простран­стве два ортонормированных базиса. Для них .  Тогда формула  принимает вид

Определение. Матрица, удовлетворяющая усло­вию , называется ортогональной.

Мы видим, что ортогональные матрицы и только они могут служить матрицами перехода от одного ортонормированного базиса к другому.

Равенство  равносильно

В силу свойств обратной матрицы отсюда вытекает, что

Это означает, что матрица  S^T будет также ортого­нальной.

Билинейные формы.

Определение. Билинейной функцией или билиней­ной формой  на линейном пространстве называется функция  от двух векторов удовлетворяющая  (для любых векторов , и и любого числа ) равен­ствам

Выберем в пространстве базис . Если

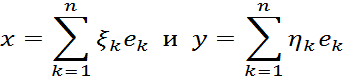
то значение билинейной формы  на векторах может быть вычислено следующим образом:

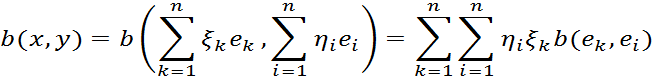
или окончательно

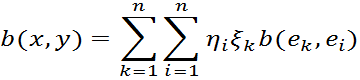
 - значения билинейной формы на всевоз­можных парах базисных векторов — называются коэф­фициентами билинейной формы, в базисе  .Их принято записывать в виде квадратной матрицы по­рядка

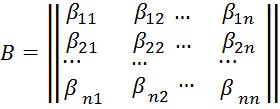
Эта матрица называется матрицей билинейной формы в данном базисе. В матричном виде, как легко прове­рить  умножением   матриц,   равенство записывается

При замене базиса матрица билинейной формы, разумеется, изменяется. Получим закон ее изменения. Пусть векторы нового базиса  и выражаются через векторы старого базиса равенствами

 

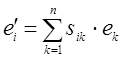
где  обозначены элементы матрицы перехода .  Для коэффициентов билинейной формы  базисе е' мы имеем при любых

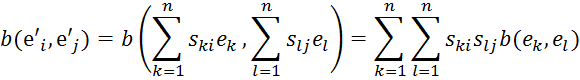
или

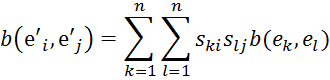
Это  равенства (3) равносильны ма­тричному равенству

в котором В' — матрица билинейной формы в базисе е'.

Билинейная форма  называется симметричной, если при любых имеет место равенство

Если билинейная форма  симметрична, то при всех , следовательно, матрица билинейной формы симметрическая. Обратно, пусть ма­трица билинейной формы симметрическая, т. е. . Тогда, поскольку квадратная матрица не меняется при  транспонировании,

следовательно, билинейная форма  симметричная. Мы доказали

Утверждение. Билинейная форма симметрична тогда и только тогда, когда ее матрица - симметриче­ская (какое бы ни был базис).

Сейчас мы переходим к изу­чению важного класса функций на линейных простран­ствах, тесно связанного с билинейными формами.

Определение. Квадратичной формой называется функция  на линейном пространстве, значение ко­торой на любом векторе определяется равенством  , где  симметричная билинейная форма линейном пространстве/

По заданной квадратичной форме линейном пространстве  однозначно опре­деляется соответствующая симметричная билинейная форма . Действительно, пусть  — произвольные векторы. Рассмотрим значение квадратичной формы на векторе :

Отсюда, используя симметричность билинейной формы, получаем

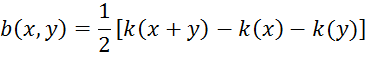
следовательно, значение  на любых двух векторах выражается через значения .

Матрица симметричной билинейной  формы  назы­вается матрицей соответствующей квадратичной формы . Значение   квадратичной формы  записывается через координаты вектора х в каком-либо базисе формулой

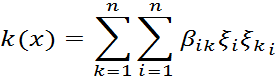
или, в матричном виде

Правая часть – однородный многочлен второй сте­пени относительно . После приведения подобных членов квадратичная форма принимает вид

Замена базиса eвлечет за собой преобразование переменных ', многочлены, получаемые один из другого такой заменой переменных при условии, считаются разными видами одной и той же квадратичной формы.

Замену переменных при условии назовем невырожденной.

Теорема 1. Для каждой квадратичной формы существует базис, в котором

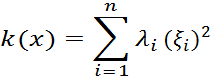
причем коэффициенты в случая вещественного прост­ранства могут принимать значения 1, -1 и 0, а в слу­чае комплексного пространства - только 1 и 0.

Kвадратичнaя  форма

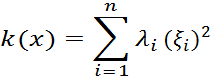
называется каноническим видом квадратич­ной формы.