Придадим
переменной tнекоторое
приращение ![]() и рассмотрим момент
и рассмотрим момент ![]() , когда точка будет в положении М1
Приращение ММ1 пути за промежуток времени
, когда точка будет в положении М1
Приращение ММ1 пути за промежуток времени ![]() обозначим через
обозначим через ![]() . Подставляя
. Подставляя ![]() вместо t, получим для
нового значения пути выражение
вместо t, получим для
нового значения пути выражение
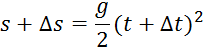
откуда
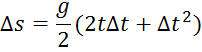
Разделив
![]() на
на ![]() , мы получим среднюю скорость
падения точки на участке ММ1
, мы получим среднюю скорость
падения точки на участке ММ1

Как
видим, эта скорость меняется вместе с изменением At, тем лучше ххарактеризуя
состояние падающей точки в момент t, чем меньше
промежуток ![]() , протекший после этого момента.
, протекший после этого момента.
Скоростью
v точки в момент
времени t называют предел, к которому стремится
средняя скорость vcp за промежуток ![]() , когда
, когда ![]() стремится к 0.
стремится к 0.
В нашем случае, очевидно,
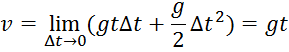
Аналогично
вычисляется скорость и и в общем случае прямолинейного движения точки.
Положение точки определяется ее расстоянием s, отсчитываемым от
некоторой начальной точки О; это расстояние и называется пройденным
путем. Время tотсчитывается
от некоторого начального момента, причем не обязательно, чтобы в этот момент
точка находилась в О. Движение считается, вполне заданным, когда
известно уравнение движения: ![]() , из которого положение точки
определяется для любого момента времени; в рассмотренном примере такую роль
играло уравнение
, из которого положение точки
определяется для любого момента времени; в рассмотренном примере такую роль
играло уравнение
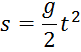
Для
определения скорости vв данный момент tпришлось бы, как
и выше, придать tприращение ![]() ; этому отвечает увеличение пути
; этому отвечает увеличение пути ![]() на
на ![]() . Отношение
. Отношение
![]()
выразит
среднюю скорость ![]() за промежуток
за промежуток ![]() . Истинная же скорость vв момент tполучится отсюда
предельным переходом:
. Истинная же скорость vв момент tполучится отсюда
предельным переходом:
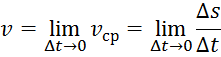
 Мы рассмотрим
ниже другую важную задачу, приводящую к подобной же предельной операции.
Мы рассмотрим
ниже другую важную задачу, приводящую к подобной же предельной операции.

рис.
Возьмем на кривой (К) (рис.), кроме точки М, еще точку М1 и проведем секущую ММ1. Когда точка M1будет перемещаться вдоль по кривой, эта секущая будет вращаться вокруг точки М.
Касательной
к кривой (К) в точке М называется предельное положение МТ секущей ММ1
когда точка М1 вдоль по кривой стремится к совпадению с М. (Смысл этого
определения состоит в том, что угол ![]() становится сколь угодно малым, лишь
только достаточно мала хорда
становится сколь угодно малым, лишь
только достаточно мала хорда ![]() .
.
Применим
для примера это определение к параболе ![]() в любой ее точке Mix, у). Так как
касательная проходит через эту точку, то для уточнения ее положения достаточно
знать еще ее угловой коэффициент.
в любой ее точке Mix, у). Так как
касательная проходит через эту точку, то для уточнения ее положения достаточно
знать еще ее угловой коэффициент.
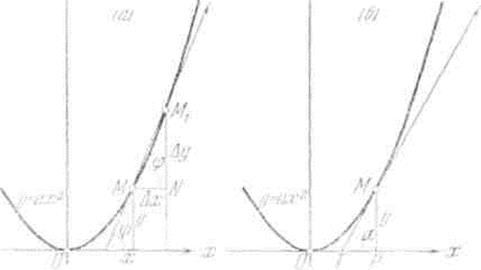
Рис.
Мы
поставим себе задачей найти угловой коэффициент ![]() касательной к точке М.
касательной к точке М.
Придав
абсциссе ![]() приращение, от точки М кривой
перейдем к точке
приращение, от точки М кривой
перейдем к точке ![]() с абсциссой
с абсциссой ![]() и ординатой
и ординатой
![]()
(рис.
а). Угловой коэффициент ![]() секущей ММ1 определится из
прямоугольного
секущей ММ1 определится из
прямоугольного ![]() MNМ1. В нем катет MNравен приращению
абсциссы
MNМ1. В нем катет MNравен приращению
абсциссы ![]() , а катет NМ1, очевидно, есть
соответствующее приращение ординаты
, а катет NМ1, очевидно, есть
соответствующее приращение ординаты
![]()
так что
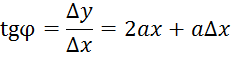
Для
получения углового коэффициента касательной, как легко понять, нужно перейти
здесь к пределу при ![]() . Мы приходим, таким образом, к
результату:
. Мы приходим, таким образом, к
результату:
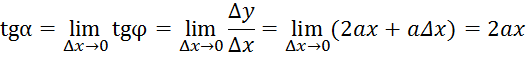
В случае любой кривой, с уравнением
![]()
угловой
коэффициент касательной устанавливается подобным образом. Приращению ![]() абсциссы
отвечает приращение
абсциссы
отвечает приращение ![]() ординаты, и отношение
ординаты, и отношение
![]()
выражает
угловой коэффициент секущей, ![]() . Угловой же коэффициент касательной получается
отсюда путём перехода к пределу при
. Угловой же коэффициент касательной получается
отсюда путём перехода к пределу при ![]() :
:
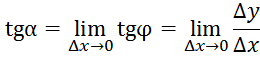
Сопоставляя операции, которые мы осуществляли при решении рассмотренных выше фундаментальных задач, легко усмотреть, что в обоих случаях - если отвлечься от различия в истолковании переменных - по существу делалось одно и то же: приращение функции делилось на приращение независимой переменной и затем вычислялся предел их отношения. Таким путем мы и приходим к основному понятию дифференциального исчисления - к понятию производной.
Пусть
функция ![]() определена в промежутке X. Исходя из
некоторого значения
определена в промежутке X. Исходя из
некоторого значения ![]() независимой переменной, придадим ему приращение
независимой переменной, придадим ему приращение ![]() , не выводящее его из промежутка X, так что и новое
значение
, не выводящее его из промежутка X, так что и новое
значение ![]() принадлежит этому промежутку. Тогда значение
принадлежит этому промежутку. Тогда значение
![]() функции заменится новым значением
функции заменится новым значением ![]() т. е. получит приращение
т. е. получит приращение
![]()
Определение. Предел
отношения приращения функции ![]() к приращению независимой переменной
к приращению независимой переменной ![]() , при стремлении
, при стремлении ![]() , т. е.
, т. е.
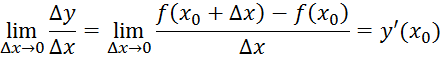
и
называется производной функции ![]() no независимой
переменной х, при данном ее значении (или в данной
no независимой
переменной х, при данном ее значении (или в данной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.