Лекция 3
Уравнение плоскости
Поверхности. Уравнение первой степени, или линейное уравнение, связывающее координаты точки в пространстве, имеет вид
![]()
причем предполагается, что коэффициенты не равны нулю
одновременно, т. е. ![]() .
.
Известно,
что через три точки не лежащих на одной прямой проходит единственная плоскость.
Возьмем произвольную точку на этой плоскости ![]() и
запишем три вектора
и
запишем три вектора ![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]()
Плоскость имеет единственную
нормаль ![]() . Из условия ортогональности получаем
систему
. Из условия ортогональности получаем
систему
![]()
![]()
![]()
Мы получили однородную систему линейных алгебраических уравнений. Условие существования нетривиального решения – равенство нулю главного определителя системы.
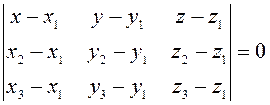
Полученное уравнение – уравнение плоскости, проходящее через три точки.
Пример. Составить уравнение плоскости проходящей через три
точки ![]() ,
, ![]()
![]()
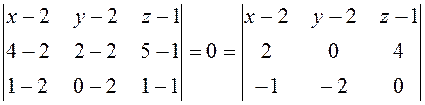
Раскрывая определитель по первой строке, получаем уравнение
![]()
И окончательно ![]()
Составим
уравнение плоскости с заданной нормалью ![]() проходящей
через заданную точку
проходящей
через заданную точку ![]() . Такая плоскость будет единственной.
Возьмем произвольную точку
. Такая плоскость будет единственной.
Возьмем произвольную точку ![]() . Чтобы эта точка принадлежала
нашей плоскости, необходимо и достаточно, чтобы вектор
. Чтобы эта точка принадлежала
нашей плоскости, необходимо и достаточно, чтобы вектор ![]() был
ортогонален нормали
был
ортогонален нормали ![]() .
.
![]()
или ![]()
Полученное уравнение – уравнение плоскости, проходящее через точку с заданной нормалью.
Теорема 1. В декартовой системе координат в пространстве каждая плоскость может быть задана линейным уравнением.
![]()
Обратно, каждое линейное уравнение в декартовой системе координат определяет плоскость.
Доказательство: запишем уравнение плоскости, проходящее через точку с заданной нормалью.
![]()
Если обозначить ![]() , то приходим к уравнению
, то приходим к уравнению
![]()
Которое является уравнением плоскости в общем виде.
Наоборот, если в уравнение плоскости
![]()
Вместо
![]() подставим
подставим ![]() , то
приходим к уравнению плоскости, проходящее через точку с заданной нормалью.
Теорема доказана.
, то
приходим к уравнению плоскости, проходящее через точку с заданной нормалью.
Теорема доказана.
Уравнения в отрезках
Плоскость
с уравнением ![]() не проходит через начало координат
в том и только в том случае, когда свободный член ее уравнения
не проходит через начало координат
в том и только в том случае, когда свободный член ее уравнения ![]() не равен нулю. В этом мы убеждаемся
сразу, подставив координаты
не равен нулю. В этом мы убеждаемся
сразу, подставив координаты ![]() в уравнение плоскости.
в уравнение плоскости.
Уравнение плоскости, не проходящей через начало координат можно представить в виде
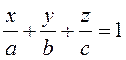
Легко
видеть, что координаты точек пересечения плоскости с осями координат будут![]() ,
, ![]()
![]() . Таким образом
. Таким образом ![]() ,
, ![]() ,
, ![]() по абсолютной величине равны
длинам отрезков, отсекаемых плоскостью на осях координат
по абсолютной величине равны
длинам отрезков, отсекаемых плоскостью на осях координат
Полученное уравнение называется уравнением плоскости в отрезках. Оно удобно, если требуется построить плоскость по ее уравнению
Угол между плоскостями
Пусть задано две плоскости
![]() и
и ![]()
Найдем
угол между плоскостями. Известно, что величина двугранного угла между
плоскостями определяется углом между нормалями этих плоскостей. Нормаль к
первой плоскости будет ![]() , ко второй плоскости -
, ко второй плоскости -
![]() . Угол между векторами определяется по
формуле
. Угол между векторами определяется по
формуле
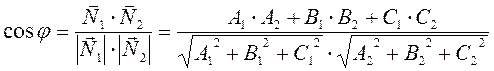
И окончательно
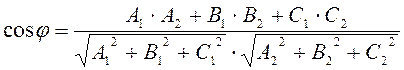
Пример.
Найти угол между плоскостями ![]() и
и ![]()
Решение. Угол между векторами определяется по формуле
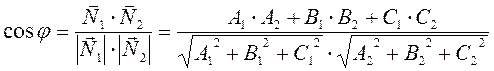
Нормаль
к первой плоскости будет ![]() , ко второй плоскости -
, ко второй плоскости -
![]() . Тогда
. Тогда
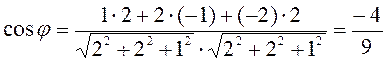
И окончательно угол между
плоскостями 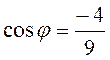
Расстояние от точки до плоскости.
Найдем
расстояние от точки ![]() до плоскости
до плоскости ![]() . Возьмем произвольную точку на плоскости
. Возьмем произвольную точку на плоскости ![]() . Составим вектор
. Составим вектор ![]() .
Спроектировав этот вектор на нормаль, мы и получим расстояние от точки до
плоскости. нормаль к нашей плоскости будет
.
Спроектировав этот вектор на нормаль, мы и получим расстояние от точки до
плоскости. нормаль к нашей плоскости будет ![]() .
.
Найдем
проекцию точки ![]() на нормаль
на нормаль
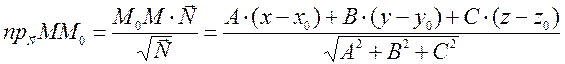
Так как точка ![]() принадлежит плоскости, то при подстановке
координат точки в уравнение плоскости оно обратится в тождество
принадлежит плоскости, то при подстановке
координат точки в уравнение плоскости оно обратится в тождество
![]()
Из этого тождества ![]() . Подставив в проекцию, получаем
. Подставив в проекцию, получаем
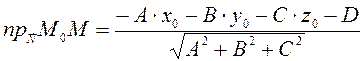
Так как расстояние величина положительная, то
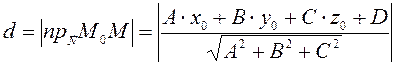
Знак
![]() не имеет геометрического смысла, так как
он зависит от того, в какую сторону направлен вектор
не имеет геометрического смысла, так как
он зависит от того, в какую сторону направлен вектор ![]() .
Однако можно заметить, что знак этот совпадает со знаком
.
Однако можно заметить, что знак этот совпадает со знаком ![]() . Если мы, смещаясь из точки в точку, не
пересекли плоскость, то
. Если мы, смещаясь из точки в точку, не
пересекли плоскость, то ![]() не изменил знака;
не изменил знака; ![]() изменит знак, если мы передвинем конец
вектора через плоскость. От сюда следует предложение, уже не зависящее от
направления вектора
изменит знак, если мы передвинем конец
вектора через плоскость. От сюда следует предложение, уже не зависящее от
направления вектора ![]() .
.
Для всех точек, лежащих по
одну и ту же сторону от плоскости, знак ![]() один и тот же. Знак этого выражения
различен для точек, лежащих по разные стороны от плоскости.
один и тот же. Знак этого выражения
различен для точек, лежащих по разные стороны от плоскости.
Пример. Найти расстояние от
точки ![]() до плоскости
до плоскости ![]()
Решение. Используя полученную
формулу, находим расстояние от точки ![]() до плоскости
до плоскости
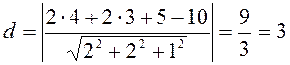
Уравнение прямой.
Составим
уравнение прямой в декартовой системе координат. Если взять точку на прямой ![]() и вектор
и вектор ![]() параллельный
этой прямой, то прямая будет определена однозначно. Возьмем произвольную точку
параллельный
этой прямой, то прямая будет определена однозначно. Возьмем произвольную точку
![]() в пространстве и запишем вектор
в пространстве и запишем вектор
![]()
Для того чтобы мочка ![]() лежала на прямой необходимо и достаточно,
чтобы вектора
лежала на прямой необходимо и достаточно,
чтобы вектора ![]() и
и ![]() были
коллинеарными. Известно, что два вектора коллинеарными необходимо, чтобы их
координаты были пропорциональны
были
коллинеарными. Известно, что два вектора коллинеарными необходимо, чтобы их
координаты были пропорциональны
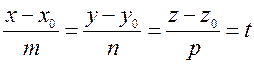
Мы получили каноническое уравнение прямой.
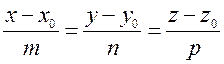
Известно,
что через две точки проходит единственная прямая. Возьмем две точки ![]() и
и ![]() и
запишем вектор
и
запишем вектор
![]()
Полученный вектор для прямой будет направляющим вектором, тогда уравнение прямой, запишется
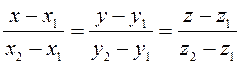
Полученное уравнение прямой называется уравнением прямой проходящей через две точки.
Прямая является пересечением двух плоскостей.
![]()
![]()
![]()
Сведем
это уравнение прямой к каноническому виду. Для этого разрешим систему относительно
![]() и
и ![]() , не
ограничивая общности считая, что
, не
ограничивая общности считая, что
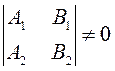
Решим систему методом Крамера
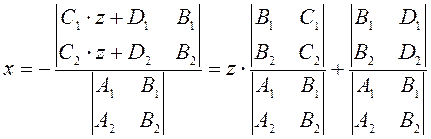
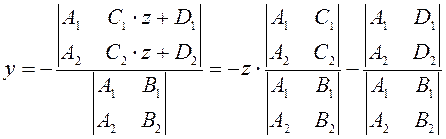
Преобразуем полученное решение
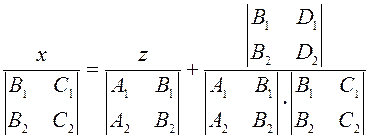 ;
; 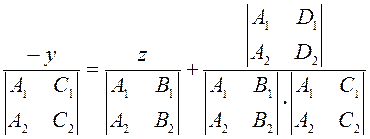
Фиксируя ![]() , получаем точку принадлежащую прямой
, получаем точку принадлежащую прямой
; 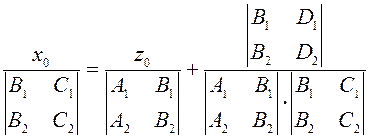 ;
; 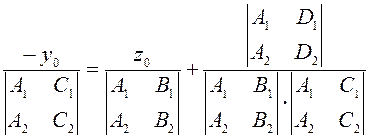
Возьмем разность
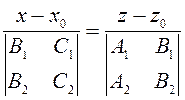 ;
; 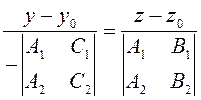
И окончательно, приходим к уравнению прямой к каноническому виду
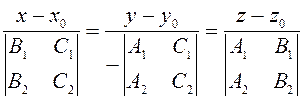
Выпишем направляющий вектор полученной прямой
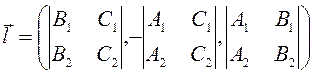
Уравнение
прямой можно записать в параметрическом виде. Если взять уравнение 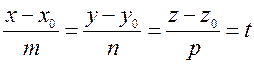 и выразить
и выразить ![]() ,
, ![]() ,
, ![]() через
параметр
через
параметр ![]() , то получим параметрическое уравнение
прямой.
, то получим параметрическое уравнение
прямой.
![]()
![]()
![]()
![]()
При решении задач иногда удобно пользоваться параметрическим уравнением прямой.
Пример.
Найти точку пересечения плоскости ![]()
и прямой 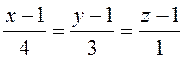 .
.
Решение. Точка пересечения плоскости и прямой является решением системы
![]()
![]()
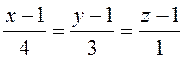 .
.
Запишем уравнение прямой в параметрическом виде
![]() ;
; ![]() ;
; ![]()
![]() Тогда наша система перепишется в виде
Тогда наша система перепишется в виде
![]()
![]()
![]()
![]()
Подставляя
![]() ,
, ![]() ,
, ![]() в уравнение плоскости, получаем
в уравнение плоскости, получаем
![]()
Приведем подобные
![]()
Тогда
![]() ;
; ![]() ;
; ![]()
И
мы получили точку ![]() пересечения плоскости и прямой .
пересечения плоскости и прямой .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.