Определение непрерывности функции в точке

Лекция 8

Определение непрерывности функции в точке.

С понятием пре­дела функции тесно связано другое важное понятие математического анализа - понятие непрерывности функции.

Рассмотрим функцию , определенную в некоторой области, пусть точка х₀ принадлежит области определения функции, так что в этой точке функция имеет определенное зна­чение .

Когда устанавливалось понятие о пределе функции при стремле­нии х к х₀

неоднократно подчеркивалось, что значения х₀ переменная  х не при­нимает; это значение могло даже не принадлежать области опре­деления функции, а если и принадлежало, то значение  при обра­зовании упомянутого предела не учитывалось.

Однако особую важность имеет именно случай, когда

Определение. Функция   непрерывна при значении  (или в точке х = х₀), если выполняется

1.  Существует

2.   Имеет место предел

если же оно нару­шено одно из этих условий, то говорят, что при этом значении (или в этой точке) функция имеет разрыв.

В случае непрерывности функции  в точке х₀ (и, очевидно, только в этом случае), при вычислении предела функции при хстановится безразличным, будет ли х в своем стремле­нии к х₀ принимать, в частности, и значение х₀, или нет.

Определение непрерывности функции можно сформулировать в других терминах. Переход от значения х₀ к другому значению х можно себе представить так,  что  значению х₀ придано   приращение  . Новое значение функции разнится от старого на приращение

Для того чтобы функция  была непрерывна в точке х₀, необходимо и достаточно, чтобы ее приращение в этой точке стремилось к 0 вместе с приращением независимой переменной. Иными словами: непрерывная функция характеризуется тем, что бесконечно малому приращению аргумента отвечает бесконечно малое же приращение функции.

Возвращаясь к основному определению, раскроем его содер­жание «на языке ». Смысл непрерывности функции  в точке х₀ сводится к следующему: каково бы ни было число , для него найдется такое число , что неравенство

  влечет за собой   

Последнее неравенство, таким образом, должно выполняться в достаточно малой окрестности  точки х₀.

Обычно мы будем в дальнейшем рассматривать функции, опреде­ленные в некотором промежутке.

Определение.  Функция непрерывна в промежутке если она непрерывна в каждой точке промежутка в отдельности.

Прежде чем перейти к примерам непрерывных функций, устано­вим следующее простое предложение, которое позволит легко рас­ширить их число.

Теорема. Если две функции  и  определены в одном и том же промемсутке и обе непрерывны в точке х₀, то в той же точке будут непрерывны и функции

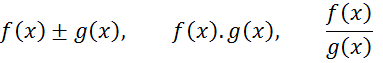
последняя функция будут непрерывна  при условии, что .

Это непосредственно вытекает из теорем о пределе суммы, разно­сти, произведения и частного двух функций, имеющих порознь пре­делы.

Остановимся для примера на частном двух функций. Предполо­жение о непрерывности функций и g(x) в точке х₀ равносильно наличию равенств

Но отсюда, по теореме о пределе частного (так как предел знаме­нателя не нуль), имеем:

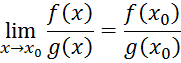
а это равенство и означает, что функция непрерывна в точке х₀.

Установим теперь понятие об односторонней непрерывности или одностороннем разрыве функции в данной точке.

Определение. Говорят, что функция  непрерывна в точке х₀ справа (слева), если выполняется предельное соотношение:

Если же то или другое из этих соотношений не осуществляется, то функция  имеет в точке х₀  разрыв, соответственно, справа или  слева.

По отношению к левому (правому) концу промежутка, в ко­тором функция определена, может идти речь, очевидно, только о непрерывности или разрыве справа (слева). Если же  есть внутренняя точка промежутка, то для непрерывности функции необходимо и достаточно, чтобы имели место сразу оба равен­ства.

Иными словами, непрерывность функции в точке  равносильна ее непрерывности в этой точке одновременно справа и слева.

Это условие непрерывности функции в точке, которое вытекает из определения.

Остановимся подробнее на вопросе о непрерывности и разрыве