Определение понятия функции. Аналитиче­ский способ задания функции

Функция называется возрастающей (убывающей) в этой области, если для любой пары принадлежащих ей значений

Если же

то функцию называют неубывающей (невозрастающей). Иногда удобнее и в этом случае называть функцию возрастающей (убывающей) - но в широком смысле.

Функции всех этих типов носят общее название монотонных. Для монотонной функции имеет место теорема, вполне аналогичная той теореме о монотонной варианте.

Теорема.  Пусть функция f(x) монотонно возрастает, хотя бы в широком смысле, в области X число а, большее всех значений (оно может быть конечным, или равным ). Если при этом функция ограничена сверху:

       (для всех х ),

то при  функция имеет конечный предел; в противном случае - она стремится к .

Доказательство. Допустим сначала, что функция огра­ничена сверху. т. е. ограничено сверху множество {} значений функции, отвечающих изменению в области . Тогда для этого множества существует конечная точная верхняя граница  . Докажем, что это число и будет искомым пределом.

Задавшись произвольным числом  , по свойству точной вер­хней границы, найдем такое значение , что . Ввиду монотонности функции, для  и подавно будет: . Так как, с другой стороны, всегда  ,то выполнится неравенство

Это и доказывает наше утверждение, стоит лишь при а конечном положить

, а при    взять

Если функция  сверху не ограничена, то, каково бы ни было число , найдется такое х', что ; тогда для  и подавно , и т. д.

Для бесконечно малых функций справедливы все утверждения, сформулированные для бесконечно малых последовательностей.

Предположим, что в каком-либо исследовании одновременно рассматривается ряд бесконечно малых величин, которые, вообще говоря, будут функциями от одной и той же пере­менной, скажем, , стремящейся к конечному или бесконечному пре­делу а.

Во многих случаях представляет интерес сравнение  бесконечно малых между собой по характеру их приближения к нулю. В основу сравнения двух бесконечно малых кладется поведение их отношения. На этот счет установим два определения:

Определение.  Если отношение (а с ним и )   имеет   конечный и отличный от нуля предел, то бесконечно малые  считают­ся величинами одного порядка.

Определение.  Если же отношение   само оказывается бесконечно малым (а обратное отношение   -   бесконечно  большим),   то   бесконечно малая  считается величиной высшего порядка, чем беско­нечно малая , и одновременно бесконечно малая  будет низшего порядка, чем бесконечно малая .

Например, если  , то по сравнению с этой бесконечно малой  одного порядка с нею будут бесконечно малая  

Найдем предел отношение этих бесконечно малых. Предварительно докажем  поле­зные неравенства.

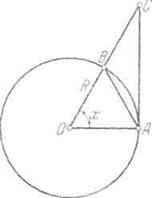
       Рис 22.

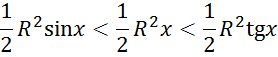
Отсюда – после сокращения на - приходим к неравенствам

Предположим,  что

разделим  sin xна  каждый  из членов неравенств. Мы получим:

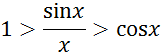
Так как

то из определения предела функции для любого сколь угодно малого   , мы получаем неравенства

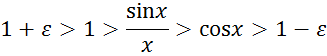
из которого следует

 

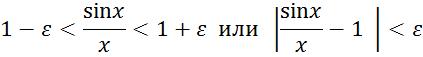
Следовательно

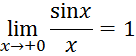
которое, очевидно, сохранится и при изменении знака , т. Е. будет справедливо для всех , лишь только .

Таким образом, бесконечно малые

   и     одного порядка малости.

Если бесконечно малая  оказывается высшего порядка,  чем бесконечно малая , то этот факт записывают так:

Таким образом,  символ    служит общим обозначением для бесконечно малой высшего порядка, чем . Этим удобным обозна­чением мы впредь будем пользоваться.

Остановимся теперь на од­ном особенно важном частном случае бесконечно малых одного порядка.

Определение.  Будем называть бесконечно малые  эквивалентными (в знаках: ), если

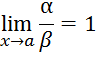
В рассмотренном примере мы получили

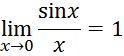
следовательно   эквивалентные бесконечно малые.

Рассмотрим еще несколько примеров.

1.  Рассмотрим предел отношения  и   

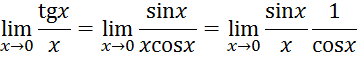
По свойствам предела функции

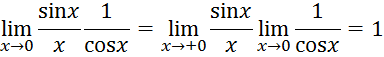
следовательно,  и  эквивалентные бесконечно малые .

2.  Рассмотрим предел   

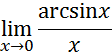
Для нахождения этого предела введем замену переменной , тогда

при этом также и  t , так как . Получим

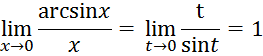
следовательно,  и  эквивалентные бесконечно малые .

3.  Рассмотрим предел  

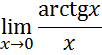
Для нахождения этого предела введем замену переменной , тогда

при этом также и  t , так как . Получим

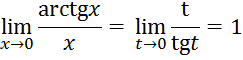
следовательно,  и  эквивалентные бесконечно малые .

4.  Рассмотрим предел  

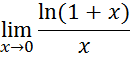
Был посчитан предел

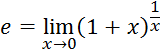
Прологарифмируем обе части этого предела по основанию е

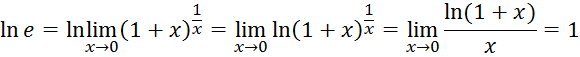
следовательно,  и  эквивалентные бесконечно малые .

5.  Рассмотрим предел  

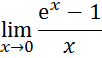
Для нахождения этого предела введем замену переменной , тогда

при этом также и  t , так как . Получим

Был посчитан предел

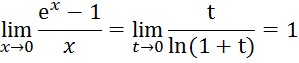
следовательно,  и  эквивалентные бесконечно малые .

Теперь выпишем цепочку эквивалентных бесконечно малых

Используя  цепочку эквивалентных бесконечно малых, зачастую, облегчает