1. Элементы дисперсионного анализа
Дисперсионный
анализ данных состоит в том, что общую дисперсию исследуемого признака ![]() разделяют на отдельные компоненты, которые
обусловлены влиянием определенных факторов. Значение фактора в дисперсионном
анализе принято называть уровнем фактора.
разделяют на отдельные компоненты, которые
обусловлены влиянием определенных факторов. Значение фактора в дисперсионном
анализе принято называть уровнем фактора.
Например, если требуется выяснить, какой вид удобрений наиболее эффективен для получения урожая, то фактор F – это удобрение, а виды удобрений – его уровни.
Основная идея дисперсионного анализа состоит в сравнении «факторной дисперсии», порождаемой воздействием фактора, и «остаточной дисперсии», обусловленной случайными причинами. Если различие между этими дисперсиями значимо, то фактор оказывает существенное влияние на Х.
Предположим, что модель, которая описывает структуру исследуемого признака, имеет вид
|
|
(1.1) |
где ![]() − значение признака
− значение признака ![]() , полученное в
, полученное в ![]() -м
эксперименте при
-м
эксперименте при ![]() -м уровне фактора;
-м уровне фактора; ![]() − среднее значение признака
− среднее значение признака ![]() ;
; ![]() −
эффект влияния фактора на значение признака
−
эффект влияния фактора на значение признака ![]() на
на ![]() -м уровне;
-м уровне; ![]() −
случайная компонента, которая влияет на значение признака
−
случайная компонента, которая влияет на значение признака ![]() в
в ![]() -м
эксперименте при
-м
эксперименте при ![]() -м уровне фактора.
-м уровне фактора.
Предположим
также, что ![]() и они взаимно независимы.
и они взаимно независимы.
При влиянии двух факторов модель будет иметь вид
|
|
(1.2) |
где ![]() − значение признака
− значение признака ![]() , полученное в
, полученное в ![]() -м
эксперименте при
-м
эксперименте при ![]() -м уровне фактора А и
на
-м уровне фактора А и
на ![]() -м уровне фактора В;
-м уровне фактора В; ![]() − среднее значение признака
− среднее значение признака ![]() ;
; ![]() −
эффект влияния фактора А на значение признака
−
эффект влияния фактора А на значение признака
![]() на
на ![]() -м
уровне;
-м
уровне; ![]() − эффект влияния фактора В на
значение признака
− эффект влияния фактора В на
значение признака ![]() на
на ![]() -м
уровне;
-м
уровне; ![]() − эффект
одновременного влияния факторов А и В;
− эффект
одновременного влияния факторов А и В; ![]() − случайная компонента.
− случайная компонента.
При проведении дисперсионного анализа исследуемый массив данных разделяют на группы, которые отличаются уровнем влияния факторов.
Анализ проводится в предположении, что исследуемый признак распределен нормально и дисперсии в каждой отдельной группе совпадают.
1.1. Однофакторный дисперсионный анализ
Рассмотрим
простейший случай, когда необходимо исследовать влияние на признак ![]() одного фактора. Результаты вычислений
представлены в табл. 1.1.
одного фактора. Результаты вычислений
представлены в табл. 1.1.
Таблица 1.1
|
Уровень фактора |
Наблюдаемое значение признака |
Групповые средние |
Общее среднее |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
Допустим,
что фактор оказывает существенное воздействие на Х.
Тогда группа наблюдаемых значений признака на одном определенном уровне
отличается от групп наблюдений на других уровнях. Следовательно, различаются и
групповые средние, причем они тем больше рассеяны вокруг общей средней, чем
большим окажется воздействие фактора. Отсюда следует, что для оценки
воздействия фактора целесообразно составить сумму квадратов отклонений
групповых средних от общей средней. Умножив эту сумму на ![]() , получим
, получим ![]() .
.
Поскольку на X кроме фактора F воздействуют и случайные причины, наблюдения одной и той же группы различны, а значит, рассеяны вокруг своей групповой средней. Следовательно, для оценки влияния случайных причин целесообразно составить сумму квадратов отклонений наблюдаемых значений каждой группы от своей групповой средней.
Для
оценки влияния и фактора, и случайных причин воспользуемся суммой квадратов
отклонений наблюдаемых значений от общей средней, то есть ![]() .
.
Расчетные формулы приведены в табл. 1.2.
Таблица 1.2
|
Вариация признака |
Сумма квадратов отклонений |
Число степеней свободы |
Статистические оценки дисперсии |
|
Внутри- групповая (остаточная) |
|
|
|
|
Меж- групповая (факторная) |
|
|
|
|
Общая |
|
|
|
Если
исследуемый фактор не влияет на значение признака ![]() , то
, то ![]() и
и ![]() можно
рассматривать как независимые оценки общей дисперсии
можно
рассматривать как независимые оценки общей дисперсии ![]() .
И наоборот, если соотношение
.
И наоборот, если соотношение ![]() и
и ![]() существенно, то в этом случае выборки
следует считать из разных совокупностей с разным уровнем фактора.
существенно, то в этом случае выборки
следует считать из разных совокупностей с разным уровнем фактора.
Пусть
![]() − дисперсия, характеризующая рассеяние
групповых внутри группы (статистическая оценка −
− дисперсия, характеризующая рассеяние
групповых внутри группы (статистическая оценка − ![]() ), а
), а ![]() − дисперсия, характеризующая рассеяние
групповых средних (статистическая оценка −
− дисперсия, характеризующая рассеяние
групповых средних (статистическая оценка − ![]() ).
).
Выдвигаем
гипотезу ![]() :
: ![]() =
= ![]() .
.
Статистический
критерий 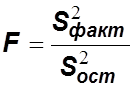 имеет распределение Фишера−Снедекора со
степенями свободы
имеет распределение Фишера−Снедекора со
степенями свободы ![]() ,
, ![]() .
.
По
значениям ![]() ,
, ![]() ,
, ![]() находим критическую точку
находим критическую точку ![]() .
.
Если
![]()
![]() , то гипотеза о влиянии
фактора на результаты исследований отвергается.
, то гипотеза о влиянии
фактора на результаты исследований отвергается.
Пример 1. Исследуется влияние трех различных видов рекламы (фактор А) на объемы продаж магазинов сотовой связи. Требуется проверить гипотезу о влиянии фактора А на результаты эксперимента с уровнем значимости 0.05.
Расчеты для проведения анализа будем выполнять в среде Microsoft Excel. Результаты расчетов показаны на рис. 1.1, формулы для проведения расчетов − на рис. 1.2.
|
|
Рис. 1.1. Расчеты для примера 1, выполненные в среде Excel |
|
|
Рис. 1.2. Расчетные формулы для примера 1 |
Лабораторная работа № 1
Однофакторный дисперсионный анализ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.