Элементы дисперсионного анализа, страница 5

Вариант 24

Вариант 25

1.2. Двухфакторный дисперсионный анализ

Предположим, что необходимо сделать вывод о влиянии двух факторов А и В на исследуемый признак Х. Для этого необходимо, чтобы исследование осуществлялось при фиксированных уровнях факторов А и В, а также при их одновременном воздействии на признак. Не ограничивая общности, можем считать, что исследования проводятся при одинаковом количестве испытаний для каждого уровня факторов А и В – n.

Пусть имеются результаты наблюдений (табл. 1.3).

Таблица 1.3

Окончание табл. 1.3

Здесь  – i-е наблюдение при j-м уровне фактора В и k-м уровне фактора А.

Обозначим через 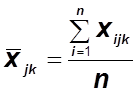 (,) среднее значение признака Х для каждого блока с фиксированными уровнями факторов А и В:

 ()– среднее значение признака по строкам;

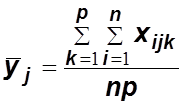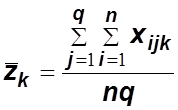()– среднее значение признака по столбцам;

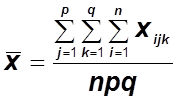 – общее среднее признака Х.

С помощью рассуждений, аналогичных проведенным в п. 1.1, получим:

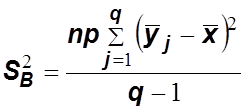 – несмещенная дисперсия, обусловленная влиянием фактора В на признак Х;

 – несмещенная дисперсия, обусловленная влиянием фактора АВ на признак Х;

 – несмещенная дисперсия, обусловленная совместным влиянием факторов А и В на признак Х;

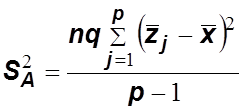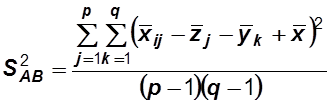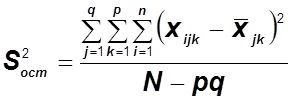 – несмещенная дисперсия, обусловленная влиянием случайных причин.

Для ответа на вопрос о влиянии (или его отсутствии) факторов А, В или совместном влиянии обоих факторов, вычисляют значения критериев: 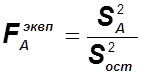; ; 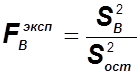 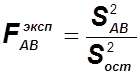и при заданном уровне значимости  находят критические точки распределения Фишера: , , .

Если , то нулевая гипотеза об отсутствии влияния фактора А на признак Х отклоняется.

Если , то нулевая гипотеза об отсутствии влияния фактора В на признак Х отклоняется.

Если , то нулевая гипотеза об отсутствии совместного влияния факторов А и В на признак Х отклоняется.

Пример 2. Результатом эксперимента является количество изготовленных рабочим деталей за единицу времени под влиянием фактора А – использования трех различных технологий изготовления деталей и фактора В – использования полуфабрикатов четырех различных производителей. Требуется проверить гипотезу о влиянии факторов А и В, а также их совместном влиянии на результаты эксперимента.

Расчеты для проведения анализа будем выполнять также в среде Microsoft Excel. Результаты расчетов приведены на рис. 1.3.

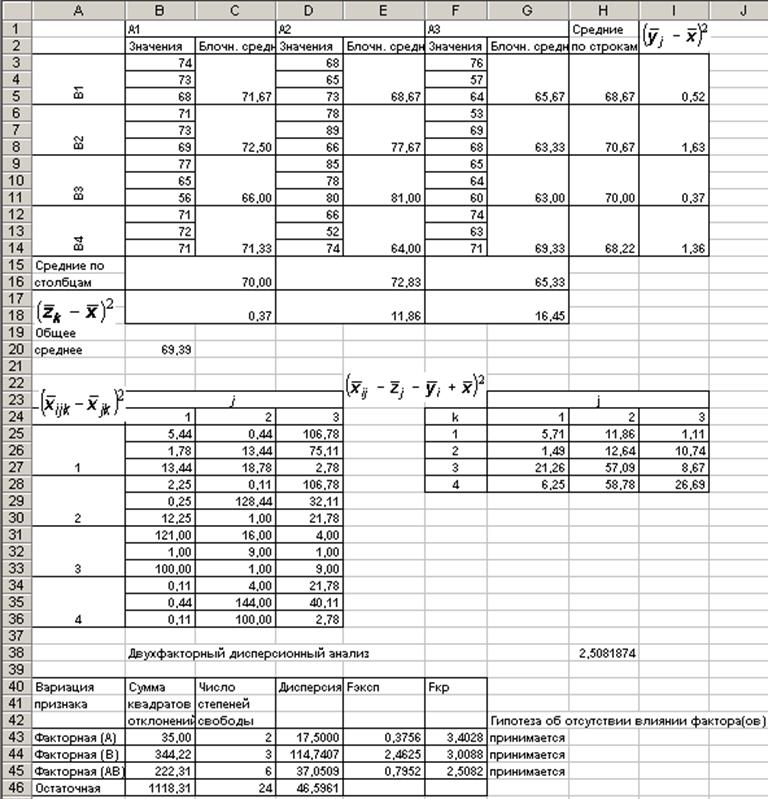
Рис. 1.3. Расчеты для примера 2

Лабораторная работа № 2

Двухфакторный дисперсионный анализ