Министерство образования и науки Украины
Национальный аэрокосмический университет им. Н.Е. Жуковского «ХАИ»
Кафедра 304
Лабораторная работа № 7
по дисциплине «Анализ данных»
Выполнила студентка гр. 335 Старцева А.В.
Проверила аспирант каф. 304 Соколова Е.О.
Харьков
2014
Элементы кластерного анализа
Метод k-средних
Постановка задачи.Рассмотреть элементы кластерного анализа на примере ирисов Фишера. Требуется реализовать алгоритм k-средних в виде компьютерной программы. Оценить полученные результаты.
Набор данных получается из файла данных "iris.dat '. Этот набор данных был собран ботаником Андерсон и содержит случайные образцы цветов, принадлежащих к трем видам ирисов setosa, лишай, и virginica. Для каждого из видов, 50 наблюдения для чашелистник длины чашелистиков, ширине, длине лепестка, и лепесток шириной записаны.
Набор данных разбивается на три группы названных setosa, лишай, и virginica. Это показано в следующем фрагменте кода.
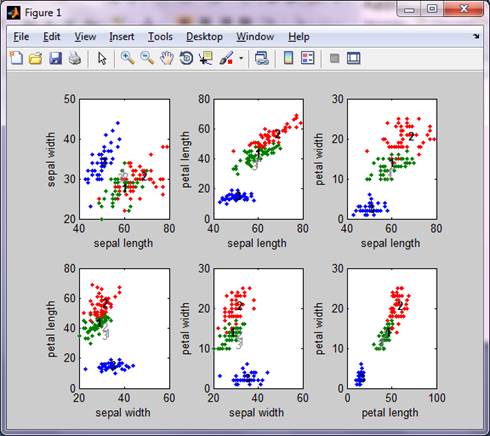
Данные, которые будут кластерные 4-мерных данных и представляет длину чашелистиков, чашелистиков ширина, длина лепестка, а лепесток ширину. От каждого из трех групп (setosa, лишай и virginica), две характеристики (например, чашелистник длина по сравнению с чашелистник ширина) цветов наносятся в 2-мерном участке. Это делается с помощью следующий фрагмент кода. На каждом шаге итерации, кластерные центры и точка ранг членства обновляются и целевая функция минимизируется, чтобы найти лучшее место для кластеров. Процесс останавливается, когда максимальное число итераций достигнуто, или когда целью улучшения функции между двумя последовательными итераций меньше минимального размера, указанного улучшение.
load iris.dat
setosa = iris((iris(:,5)==1),:); % данных для setosa
versicolor = iris((iris(:,5)==2),:); % данных для лишай
virginica = iris((iris(:,5)==3),:); % данных для virginica
obsv_n = size(iris, 1); % общее число наблюдений
Characteristics = {'sepal length','sepal width','petal length','petal width'};
pairs = [1 2; 1 3; 1 4; 2 3; 2 4; 3 4];
h = figure;
for j = 1:6,
x = pairs(j, 1);
y = pairs(j, 2);
subplot(2,3,j);
plot([setosa(:,x) versicolor(:,x) virginica(:,x)],...
[setosa(:,y) versicolor(:,y) virginica(:,y)], '.');
xlabel(Characteristics{x},'FontSize',10);
ylabel(Characteristics{y},'FontSize',10);
end
cluster_n = 3; % Количество кластеров
expo = 2.0; % Экспонента U
max_iter = 100; % Макс. итерация
min_impro = 1e-6; % Мин. улучшение
% Инициализации нечеткой раздел
U = initfcm(cluster_n, obsv_n);
% График данные, если окно цифра закрыт
if ishghandle(h)
figure(h);
else
for j = 1:6,
x = pairs(j, 1);
y = pairs(j, 2);
subplot(2,3,j);
plot([setosa(:,x) versicolor(:,x) virginica(:,x)],...
[setosa(:,y) versicolor(:,y) virginica(:,y)], '.');
xlabel(Characteristics{x},'FontSize',10);
ylabel(Characteristics{y},'FontSize',10);
end
end
% Итерации
for i = 1:max_iter,
[U, center, obj] = stepfcm(iris, U, cluster_n, expo);
fprintf('Iteration count = %d, obj. fcn = %f\n', i, obj);
% Центры Обновить
if i>1 && (abs(obj - lastobj) < min_impro)
for j = 1:6,
subplot(2,3,j);
for k = 1:cluster_n,
text(center(k, pairs(j,1)), center(k,pairs(j,2)), int2str(k), 'FontWeight', 'bold');
end
end
break;
elseif i==1
for j = 1:6,
subplot(2,3,j);
for k = 1:cluster_n,
text(center(k, pairs(j,1)), center(k,pairs(j,2)), int2str(k), 'color', [0.5 0.5 0.5]);
end
end
end
lastobj = obj;
end
>> Untitled4
Iteration count = 1, obj. fcn = 28858.122927
Iteration count = 2, obj. fcn = 20630.279236
Iteration count = 3, obj. fcn = 13991.757133
Iteration count = 4, obj. fcn = 8376.023429
Iteration count = 5, obj. fcn = 6789.945484
Iteration count = 6, obj. fcn = 6378.219364
Iteration count = 7, obj. fcn = 6205.147592
Iteration count = 8, obj. fcn = 6125.249246
Iteration count = 9, obj. fcn = 6088.297601
Iteration count = 10, obj. fcn = 6071.590995
Iteration count = 11, obj. fcn = 6064.222106
Iteration count = 12, obj. fcn = 6061.035582
Iteration count = 13, obj. fcn = 6059.676957
Iteration count = 14, obj. fcn = 6059.103196
Iteration count = 15, obj. fcn = 6058.862415
Iteration count = 16, obj. fcn = 6058.761785
Iteration count = 17, obj. fcn = 6058.719840
Iteration count = 18, obj. fcn = 6058.702387
Iteration count = 19, obj. fcn = 6058.695133
Iteration count = 20, obj. fcn = 6058.692120
Iteration count = 21, obj. fcn = 6058.690869
Iteration count = 22, obj. fcn = 6058.690350
Iteration count = 23, obj. fcn = 6058.690135
Iteration count = 24, obj. fcn = 6058.690045
Iteration count = 25, obj. fcn = 6058.690008
Iteration count = 26, obj. fcn = 6058.689993
Iteration count = 27, obj. fcn = 6058.689987
Iteration count = 28, obj. fcn = 6058.689984
Iteration count = 29, obj. fcn = 6058.689983
Iteration count = 30, obj. fcn = 6058.689982
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.