Элементы регрессионного анализа

5. Элементы регрессионного анализа

Корреляционный и дисперсионный анализы позволяют сделать вывод о том, существует ли функциональная зависимость между переменными и какой вид она имеет (линейный, нелинейный). Однако  исследователю необходимо знать явный вид зависимости, например:

;

;

.

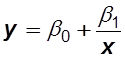Такие зависимости называются функциями регрессии. Форму эмпирической связи можно исследовать с помощью корреляционных полей, когда на плоскость наносятся точки .

На практике обычно  зависит от множества переменных  (а не от одной). В этом случае регрессия называется линейной множественной и ее уравнения имеют вид

,            (5.1)

где .

В матричной форме уравнения (5.1) можно переписать так:

,

где 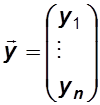, , 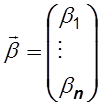,  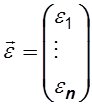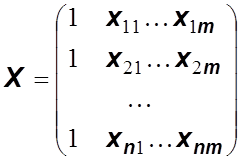– матрица размером .

Матрица  называется регрессионной матрицей.

Параметры  оцениваются с помощью статистических оценок , которые получают после статистической обработки результатов выборки.

Для нахождения параметров  воспользуемся методом наименьших квадратов:

;

;

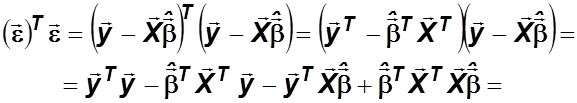
, следовательно,

()+.

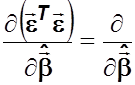Известно, что ,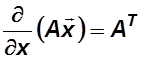

= .

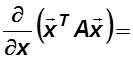
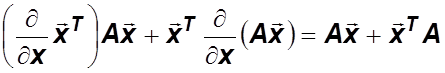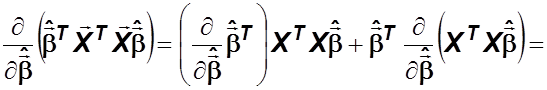
Тогда

.

Отсюда ++;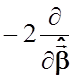

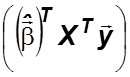Найдем доверительные интервалы для значений функции множественной линейной регрессии.

Рассмотрим корреляционную матрицу вектора :

;

;

;

Таким образом, имеем

.

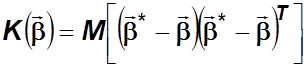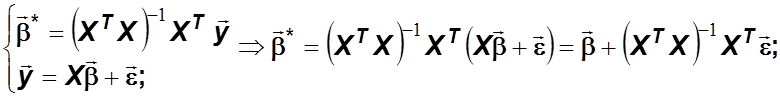
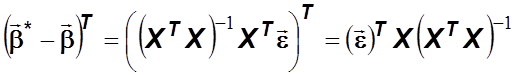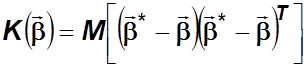
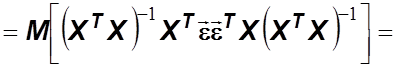
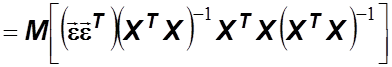
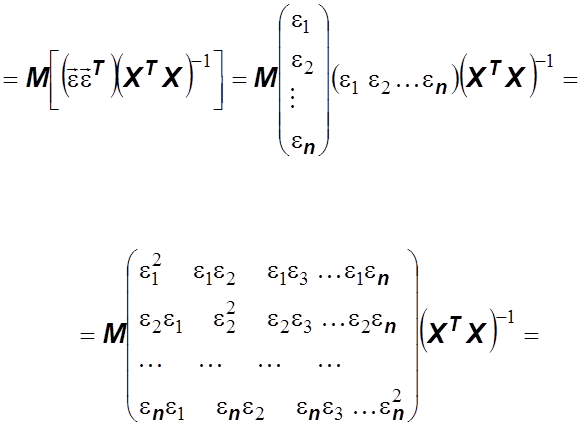
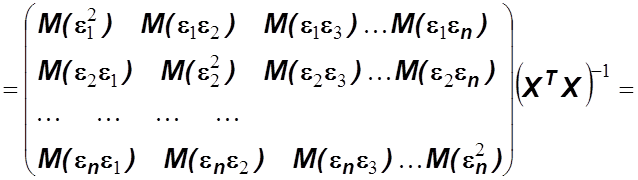
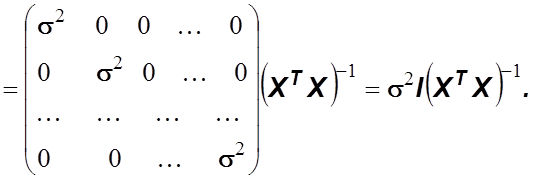
(5.2)

Поскольку  – неизвестная величина, вместо нее используют ее несмещенную точечную оценку:

,

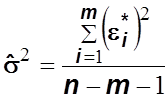где  – количество наблюдений, а  – количество оцениваемых параметров множественной линейной регрессии.

Используя свойства дисперсии от суммы зависимых случайных величин, получаем:

.

С помощью (5.2) получим

.

Таким образом, истинное значение  находится в интервале

.

(5.3)

Если в уравнения множественной регрессии переменные  входят в виде , то регрессия называется нелинейной. В общем случае нелинейная регрессия записывается с помощью уравнений вида

,

(5.4)

где параметры  являются неизвестными постоянными коэффициентами, которые подлежат статистическим оценкам, а .

Систему уравнений (5.4) перепишем в матричной форме:

,

где , , , .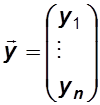

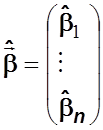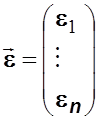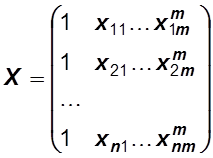Осуществив преобразования, аналогичные проведенным для линейного случая, получим

.

Иногда на практике возникает необходимость рассмотреть нелинейную модель с параметрами, например, такого вида:

.

(5.5)

Для учета влияния случайных факторов введем случайную величину .

Статистической оценкой уравнения (5.5) будет регрессионное уравнение вида

.

(5.6)

Прологарифмируем уравнение (5.6):

,

которое в матричном виде можно переписать так:

,

где , , , .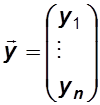

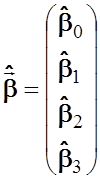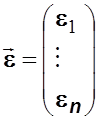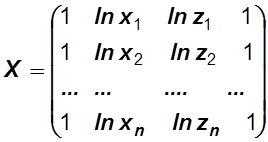Воспользовавшись выкладками, проведенными для линейного случая, получим

.

Пример 7. Дана выборка из генеральной совокупности (табл. 5.1).

Таблица    5.1

№ п/п	y	x	z	t
1	3.42	4.12	1.93	1
2	3.16	4.01	1.89	2
3	3.04	3.76	1.82	3
4	2.9	3.48	1.75	4
5	3.04	3.43	1.72	5
6	2.83	3.02	1.68	6
7	2.73	2.97	1.68	7
8	2.81	2.91	1.72	8
9	2.92	2.84	1.75	9
10	2.98	2.74	1.81	10
11	2.90	2.68	1.84	11
112	3.12	2.76	1.92	12
13	3.32	2.81	1.95	13
14	3.35	2.89	1.97	14
15	3.41	2.96	2.03	15

По данным выборки требуется:

1. Найти точечные статистические оценки  для параметров  функции регрессии .

2. С надежностью  построить доверительный интервал для функции регрессии .

3. Вычислить коэффициент множественной регрессии.

Вычисления проведем в пакете математических вычислений MATLAB. Необходимые инструкции запишем в m-файл regr.m, содержимое которого показано на рис. 5.1.

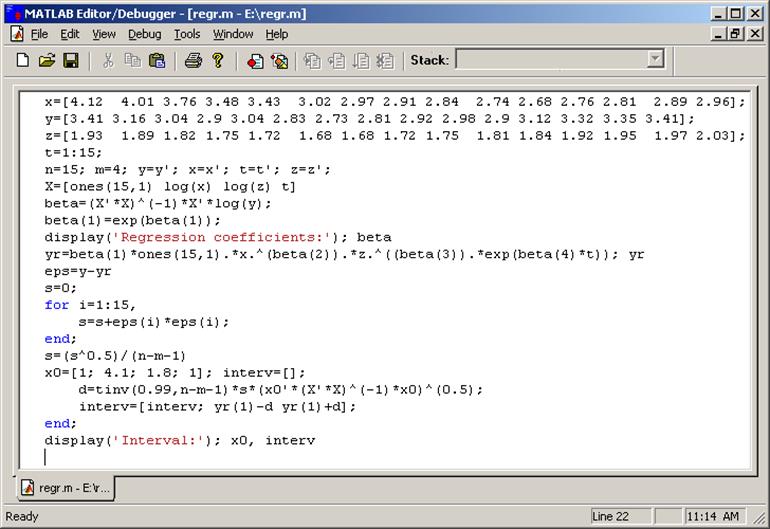
Рис. 5.1. Окно редактора m-файлов

Фрагмент диалогового окна среды MATLAB с полученными результатами изображен на рис. 5.2.

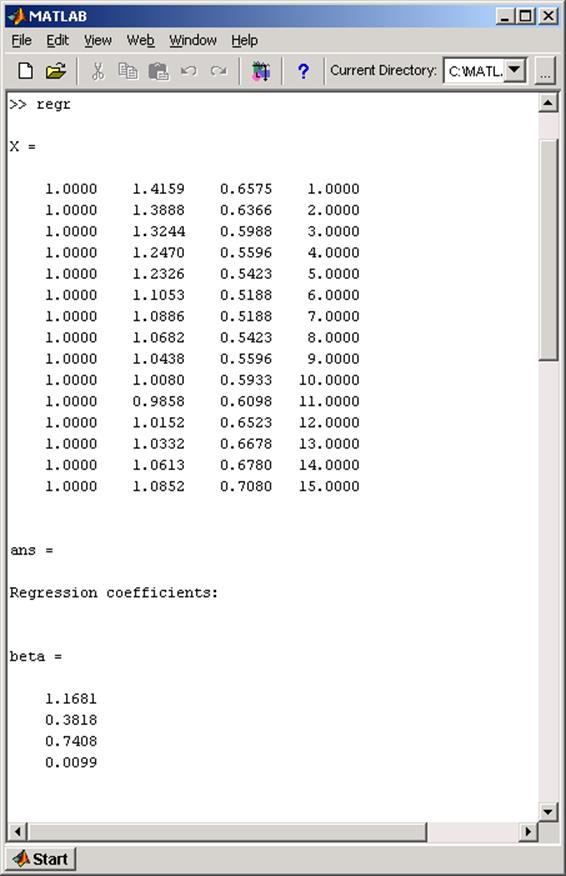
Рис. 5.2. Вывод результатов

Лабораторная работа №4

Линейная множественная регрессия

Постановка задачи. Требуется:

1. Найти точечные статистические оценки  для параметров  функции регрессии .

2. С надежностью  построить доверительный интервал для функции регрессии.

3. Вычислить коэффициент множественной регрессии.

Ниже приведена зависимость себестоимости одной тонны литья стали , грн, от выработки литья на одного работающего , т, брака литья , %, и среднего уровня оплаты труда , тыс. грн/год, для 10 сталелитейных предприятий.

Варианты заданий

Вариант 1