Элементы корреляционного анализа. Ранговая корреляция. Корреляция категоризованных переменных

Выборочной ковариационной матрицей  многомерной случайной величины  называется матрица , где

Здесь  –  значение -го признака в -м наблюдении,  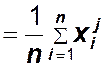– выборочные средние значения случайных величин .

Ковариационная матрица содержит сведения о степени случайного разброса анализируемых переменных, а также о характере и структуре статистических взаимосвязей между ними. Из определения следует, что она является симметрической и положительно определенной.

Выборочный парный коэффициент корреляции  измеряет степень тесноты линейной связи между переменными  и  и определяется по формуле

Парный коэффициент корреляции может принимать значения от –1 до +1, причем для статистически независимых величин он равен нулю, но из равенства нулю этого коэффициента не следует независимости переменных, а следует отсутствие линейной зависимости (может иметь место нелинейная зависимость). Из факта  следует, что переменные  и  связаны чисто функциональным линейным отношением, т. е. , где  и  – некоторые константы.

Для проверки статистически значимого отличия от нуля величины выборочного парного коэффициента корреляции, то есть для проверки гипотезы

используется статистика

которая распределена как стьюдентовская случайная величина  с  степенями свободы, т. е. если выполняется условие

то гипотеза  отвергается с вероятностью .

Интервальная оценка парного коэффициента корреляции при уровне доверия =  строится по формуле

где 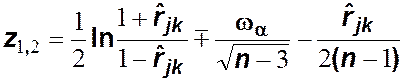 (– аргумент функции Лапласа, такой, что ).

Парное корреляционное отношение  является измерителем степени тесноты нелинейной связи, существующей между количественной переменной  (результирующей переменной y) и переменной  (объясняющей признак х), выборочное парное корреляционное отношение определяется формулой

где  – число интервалов группирования по оси ;

 – число наблюдений двумерной случайной величины (,), попавшей в -й интервал группирования;

 – -е наблюдаемое значение переменной  в -м интервале группирования ();

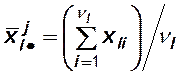  – условное среднее , посчитанное по наблюдениям, попавшим в -й интервал группирования;

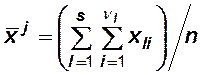 – общее среднее , посчитанное по всем наблюдаемым значениям.

 может принимать значения в диапазоне от 0 до 1; значение = 0 свидетельствует об отсутствии какой бы то ни было связи между переменными, если же = 1, то между  и  существует чисто функциональная связь.

Корреляционные отношения несимметричны, т. е. . Другими словами, значение этой характеристики зависит от того, какую из двух переменных интерпретируют в качестве зависимой переменной.

Для проверки статистически значимого отличия от нуля величины выборочного парного корреляционного отношения, т. е. для проверки гипотезы , используется статистика

,

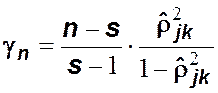которая распределена как -распределенная случайная величина, т. е. если окажется, что

,

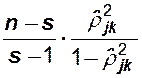
то гипотеза  отвергается с вероятностью ошибки .

Интервальная оценка при уровне доверия  для парного корреляционного отношения строится по формуле

,

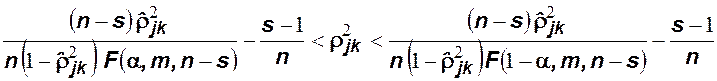где 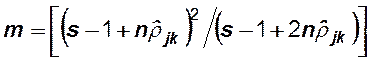 ([x] обозначает целую часть числа х).

Множественные корреляционные связи – это связи между более чем двумя переменными (в отличие от парных). Специфика множественных связей заключается в том, что при их анализе возникает необходимость измерять степень тесноты связи между переменными, а также возникают трудности с интерпретацией парных коэффициентов (так как на связь могут влиять другие переменные, не учтенные нами). Это обстоятельство делает необходимым введение таких измерителей статистической связи, которые были бы «очищены» от влияния других, т. е. давали бы оценку связи между переменными при фиксированных значениях остальных. В таком случае говорят о статистическом анализе частных связей и используют частные коэффициенты корреляции – , которые измеряют степень тесноты линейной связи между переменными  и , когда значения переменных  зафиксированы на их средних уровнях. В общем случае для подсчета этих характеристик необходимо было бы иметь выборку специальной структуры, обеспечивающей хотя бы несколько наблюдений при фиксированном значении каждой из «мешающих» переменных . Однако если исследуемые переменные подчиняются (р+1)-мерному нормальному закону, то для подсчета значений  может быть использована формула

где  – алгебраическое дополнение элемента  в выборочной корреляционной матрице .

При проверке гипотез = 0 и при построении доверительных интервалов следует пользоваться теми же правилами, что и для обычных (парных) коэффициентов корреляции  с одной поправкой: объем выборки заменить с  на .