Элементы корреляционного анализа. Ранговая корреляция. Корреляция категоризованных переменных, страница 6

3. Ранговая корреляция

Ранговая корреляция предназначена для изучения корреляционной связи между различными упорядочениями (ранжировками) объектов по степени проявления того или иного свойства. Пусть  – результат ранжировки  объектов по -му признаку. Компонента  определяет то порядковое место, которое присвоено -му объекту в общем ряду  анализируемых объектов. При этом другая ранжировка  может интерпретироваться как упорядочение по другому (-му) свойству либо как упорядочение по тому же свойству другим экспертом.

Ранговый коэффициент корреляции Спирмэна  является измерителем степени согласованности двух различных ранжировок  и  одного и того же множества, состоящего из  объектов. Его выборочное значение определяется формулой

Ранговый коэффициент корреляции Спирмэна может принимать значения в диапазоне от –1 до +1. Значение –1 достигается при противоположных ранжировках, а значение +1 – при совпадающих. Нулевые значения свидетельствуют об отсутствии статистической связи между ранжировками.

Пример 4. Два эксперта проранжировали качество изделий, изготовленных на 10 предприятиях. Пронумеровав проекты в порядке ранжировки первого эксперта, получим:

 = (1; 2; 3; 4; 5; 6; 7; 8; 9; 10);  = (2; 3; 1; 4; 6; 5; 9; 7; 8; 10).

Требуется оценить степень согласованности мнений двух экспертов, используя в качестве измерителя ранговый коэффициент корреляции Спирмэна.

Решение.

,

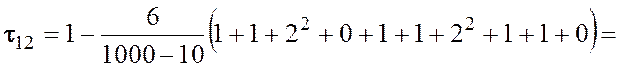
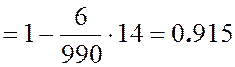что свидетельствует о существенной положительной ранговой связи между исследуемыми переменными.

В ситуациях, когда в той или иной ранжировке наблюдается «дележка мест», например, в -й ранжировке три объекта разделили места со 2-го по 4-е. В этом  случае объектам, разделившим места, приписывается ранг, равный среднему арифметическому соответствующих разделенных мест, например: .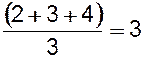

Пусть  – количество групп с неразличимыми рангами в -й ранжировке;

 – количество элементов, входящих в -ю группу неразличимых рангов в -й ранжировке;

.

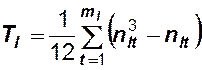В случае связанных рангов формула для вычисления коэффициента Спирмэна будет иметь вид

Пример 5. Десять школьников были протестированы по двум дисциплинам ( и ), и на основе набранных баллов получены следующие две ранжировки:  = (1; 2.5; 2.5; 4.5; 4.5; 6.5; 6.5; 8; 9.5; 9.5);  = (1; 2; 3; 4.5; 4.5; 6; 8; 8; 8; 10). С помощью рангового коэффициента корреляции Спирмэна оценить степень согласованности ранжировок.

Решение.

Проверка гипотезы  о полном отсутствии статистической связи в двух анализируемых ранжировках при  проводится с помощью статистики 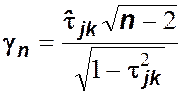, которая распределена как стьюдентовская случайная величина  с  степенями свободы.

В случае

 >

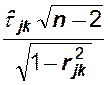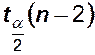
гипотеза отвергается с вероятностью ошибки .

При  гипотеза  проверяется, используя таблицу для проверки статистической значимости корреляционной связи с помощью рангового коэффициента корреляции Спирмэна, по которой находим значение 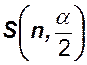. Критическое значение находится по формуле .

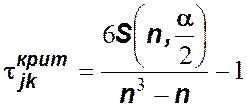Если 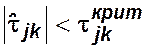, то гипотезу  отвергают с вероятностью ошибки .

Коэффициент конкордации (согласованности) Кендалла  является измерителем тесноты статистической связи, существующей между  различными ранжировками , .

Этот коэффициент может принимать значения в диапазоне от 0 (что соответствует полному отсутствию статистической связи между анализируемыми ранжировками) до 1 (что означает полное совпадение всех анализируемых ранжировок).

При наличии связных рангов формула имеет вид