Элементы корреляционного анализа. Ранговая корреляция. Корреляция категоризованных переменных, страница 7

.

Проверка гипотезы :  при  проводится с использованием статистики , которая распределена как .

При  проверка гипотезы осуществляется с помощью таблиц критических значений статистики  при заданном уровне значимости .

Если 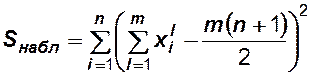, то гипотеза  должна быть отвергнута с вероятностью ошибки .

4. Корреляция категоризованных переменных

Признак называется категоризованным, если его возможные значения описываются конечным числом состояний (например, «неудовлетворительно», «удовлетворительно», «хорошо», «отлично»).

Статистический анализ связей между категоризованными переменными  и  проводится с помощью двухвходовых таблиц сопряженности (табл. 4.1).

Таблица 4.1

Градации признака	Градации признака
	1	2	...		...
1			...		...
2			...		...
. . .	. . .	. . .	...	. . .	...	. . .	. . .
			...		...
. . .	. . .	. . .	...	. . .	...	. . .	. . .
			...		...
			...		...

В табл. 4.1 представлены результаты статистического обследования  объектов по категоризованным признакам  и . В ней  обозначает количество объектов, у которых наблюдалось значение признака  на -м уровне, а значение признака   – на - м уровне.

Величины  и  вычисляются по формулам

,

.

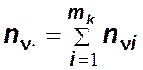Коэффициент квадратической сопряженности  категоризованных признаков  и  является измерителем степени их статистической взаимосвязи:

.

(4.1)

Значение  может меняться от 0 до .

Проверка гипотезы : = 0 осуществляется с помощью статистики , которая распределена как -распределенная случайная величина.

Пример 6. Дано распределение 678 студентов по значениям двух анализируемых категоризованных признаков: по качеству жилищных условий () и успеваемости (). Были определены четыре градации по первому признаку: «очень хорошо», «хорошо», «удовлетворительно», «плохо» и четыре градации по второму признаку: «плохая»,  «средняя», «высокая», «отличная» (табл. 4.2).

Таблица 4.2

Требуется вычислить выборочное значение  и проверить гипотезу об отсутствии статистической связи между успеваемостью и качеством жилищных условий студентов с уровнем значимости 0.05.

Решение.

.

Сформулируем нулевую гипотезу:

.

Определяем критическое значение  .

Поскольку , гипотеза об отсутствии статистической связи между успеваемостью и качеством жилищных условий принимается.

Информационная мера связи  между категоризованными переменными  и , так же как и коэффициент квадратической сопряженности, является измерителем степени их статистической взаимосвязи. Ее выборочное значение определяется по формуле

.

(4.2)

Ее значение может меняться от нуля до . Проверка гипотезы : = 0 о статистической независимости переменных  и  осуществляется с помощью статистики , которая распределена как -распределенная случайная величина.