Элементы корреляционного анализа. Ранговая корреляция. Корреляция категоризованных переменных, страница 2

Множественный коэффициент корреляции  используется в качестве измерителя степени тесноты статистической связи между результирующим показателем  и набором объясняющих переменных  при линейной форме регрессионной зависимости . Множественный выборочный коэффициент корреляции может быть вычислен по матрице парных коэффициентов корреляции :

где  – номер объясняющей переменной среди переменных .

Квадрат множественного коэффициента корреляции называется коэффициентом детерминации  и определяет долю общей вариации результирующего признака  в линейном варианте соотношения , объясненную изменением функции регрессии.

Проверка гипотезы  (т. е. проверка гипотезы об отсутствии линейной связи между  и совокупностью переменных ) осуществляется с помощью статистики

,

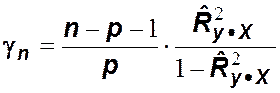которая в условия справедливости гипотезы  должна «вести себя» как  -распределенная случайная величина.

Пример 3. Имеются данные об уровне механизации работ  (%), уровне оплаты труда  (от 1 до 5), производительности труда  (т/ч):

Требуется:

1) оценить средние значения , среднеквадратические отклонения  и корреляционную матрицу  анализируемого трехмерного признака;

2) вычислить матрицу выборочных частных коэффициентов корреляции 1-го порядка, т. е. оценить значения коэффициентов ;

3) проверить гипотезы при уровне значимости  о статистически незначимом отличии от нуля выборочных парного и частного коэффициентов корреляции, соответственно  и , и построить для них интервальные оценки с доверительной вероятностью ;

4) найти точечную оценку  множественного коэффициента корреляции  и проверить гипотезу при уровне значимости  о его статистически незначимом отличии от нуля.

Расчеты проведем в пакете математических вычислений MathCad. Результаты расчетов показаны на рис. 2.1 – 2.4.

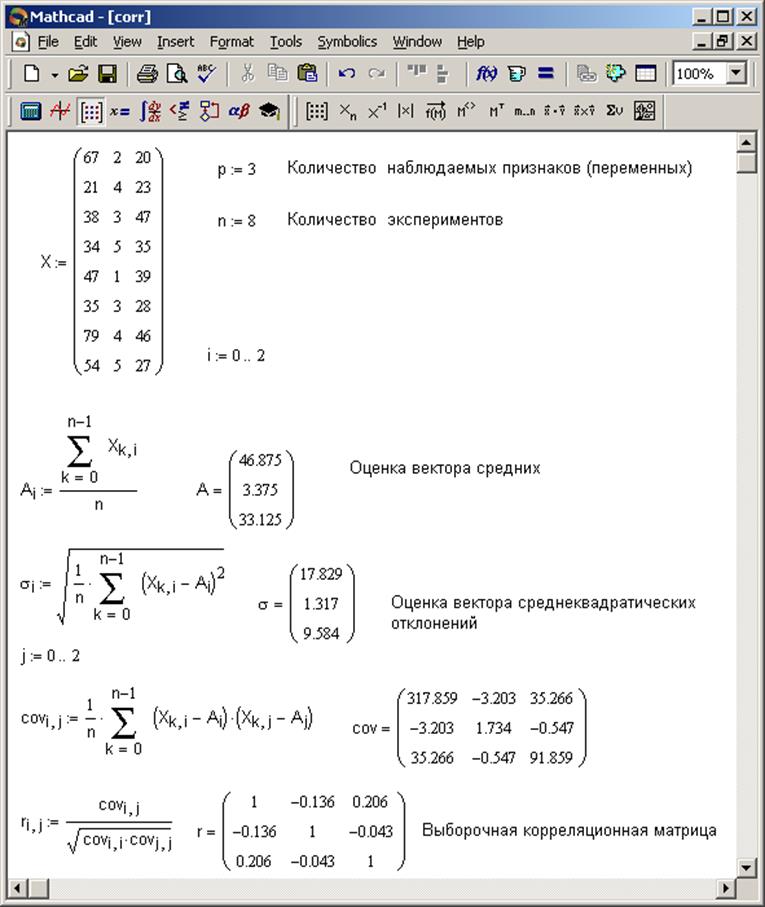
Рис. 2.1. Результаты вычислений оценок вектора средних, среднеквадратических отклонений и корреляционной матрицы

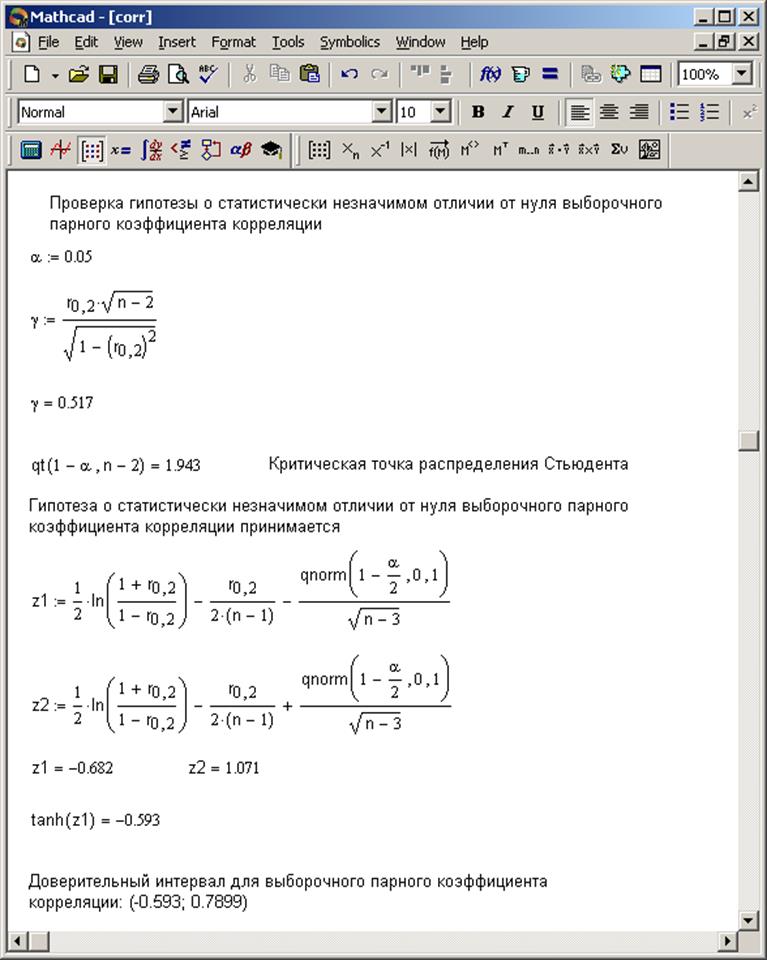
Рис. 2.2. Результаты проверки нулевой гипотезы для парного коэффициента корреляции и построения для него интервальной оценки

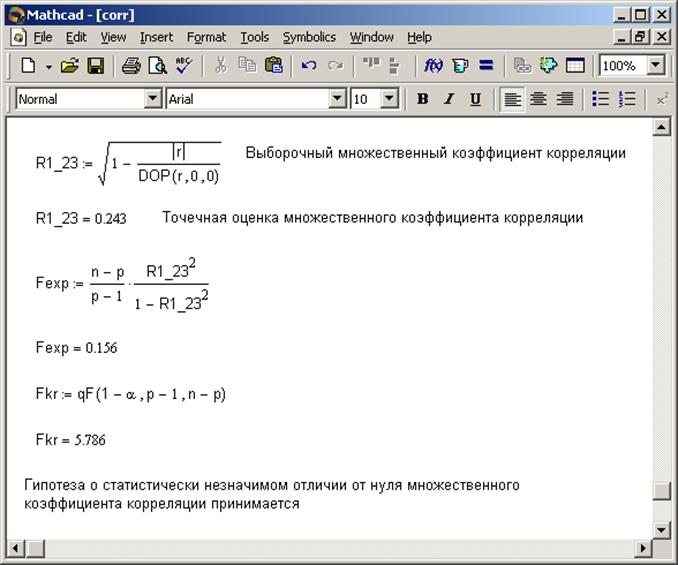
Рис. 2.3. Результаты проверки нулевой гипотезы для частного коэффициента корреляции и построения для него интервальной оценки

Рис. 2.4. Результаты расчетов множественного коэффициента корреляции и проверки гипотезы о его статистически незначимом отличии от нуля

Лабораторная работа № 3

Элементы корреляционного анализа

Постановка задачи. Для восьми предприятий, производящих прокат, измерены процентное содержание углерода (), никеля () и кремния () в стали. Значения (, , ) образуют выборку из трехмерной генеральной совокупности. Требуется:

1) оценить средние значения , среднеквадратические отклонения  и корреляционную матрицу  анализируемого трехмерного признака;

2) вычислить матрицу выборочных частных коэффициентов корреляции 1-го порядка, т. е. оценить значения коэффициентов ;

3) проверить гипотезы при уровне значимости  о статистически незначимом отличии от нуля выборочных парного и частного коэффициентов корреляции, соответственно  и , и построить для них интервальные оценки с доверительной вероятностью ;

4) найти точечную оценку  множественного коэффициента корреляции  и проверить гипотезу при уровне значимости  о его статистически незначимом отличии от нуля.

Данные по процентному содержанию углерода, никеля и кремния в стали приведены ниже по вариантам.

Варианты заданий

Вариант 1