















3. Решение задач
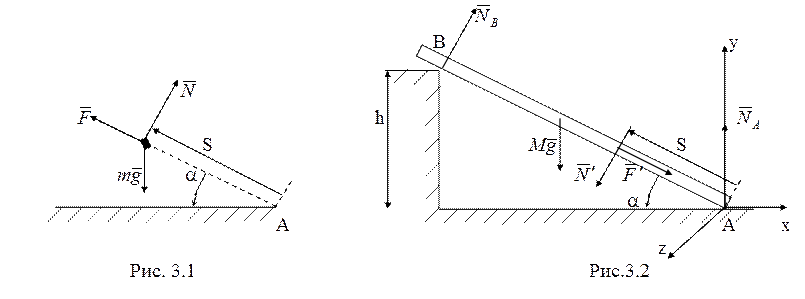 |
Для движения мыши ![]() в траекторной системе координат второй закон
Ньютона дает уравнения
в траекторной системе координат второй закон
Ньютона дает уравнения
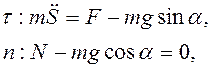 т.е.
т.е. 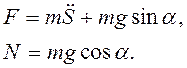 (3.1)
(3.1)
Условия равновесия доски в системе
координат ![]() ведут к уравнениям статики
ведут к уравнениям статики
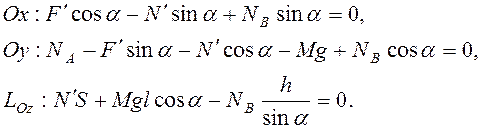 (3.2)
(3.2)
Так как ![]() , то,
учитывая (3.1),
, то,
учитывая (3.1),
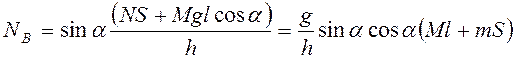 .
.
Подстановка ![]() в
первое уравнение системы (3.2) ведет к уравнению
в
первое уравнение системы (3.2) ведет к уравнению
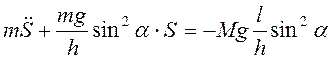 . (3.3)
. (3.3)
Соответствующие начальные условия
![]() . (3.4)
. (3.4)
Общее решение линейного неоднородного уравнения (3.3) имеет вид
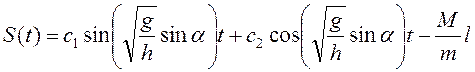 .
.
Из начальных условий (3.4) получим,
что 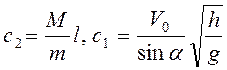 . В итоге
. В итоге
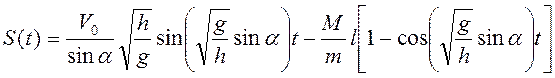 .
.
Замечание. Второе уравнение системы (3.2) не
использовалось. Оно позволяет в рассматриваемом случае движения найти силу
реакции опоры ![]() .
.
2) Перепишем уравнение
(3.3) в виде 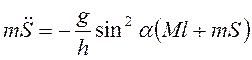 . Так как
. Так как 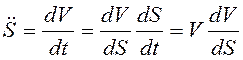 ,
то
,
то 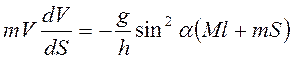 . Разделяя переменные и
. Разделяя переменные и
интегрируя последнее уравнение на участке движения АВ, получим
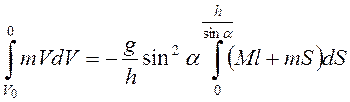 ,
и далее
,
и далее 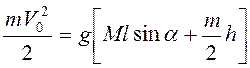 , т.е.
, т.е.
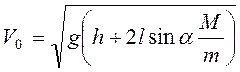 .
.
Ответ: 1) 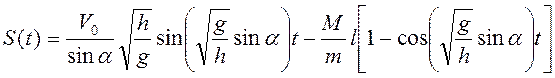 ,
,
2) 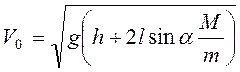 .
.
2. Точка движется в
плоскости, проходящей через вектор начальной скорости и радиус шара,
проведенный в начальное положение точки, описывая дугу окружности радиуса ![]() в этой плоскости (рис. 3.3). Учитывая действующие
на точку силы
в этой плоскости (рис. 3.3). Учитывая действующие
на точку силы ![]() , нормальную реакцию опоры
, нормальную реакцию опоры ![]() и силу трения
и силу трения ![]() ,
запишем второй закон Ньютона в проекции на касательную и нормаль к траектории
точки.
,
запишем второй закон Ньютона в проекции на касательную и нормаль к траектории
точки.

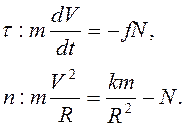 (3.5)
(3.5)
Реакция опоры 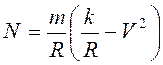 .
При
.
При 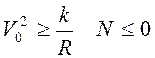 , что невозможно, т.е. при достаточно
большой начальной скорости
, что невозможно, т.е. при достаточно
большой начальной скорости ![]() точка в начальный момент
времени отрывается от поверхности шара.
точка в начальный момент
времени отрывается от поверхности шара.
Подстановка в первое уравнение системы (3.5) дает
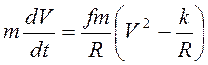 , или
, или 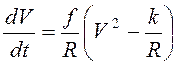 . Разделяя
переменные, имеем
. Разделяя
переменные, имеем
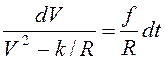 .
Интегрируя последнее выражение на участке движения от его начала до остановки,
получим
.
Интегрируя последнее выражение на участке движения от его начала до остановки,
получим
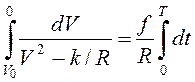 . (3.6)
. (3.6)
Интеграл в левой части (3.6)
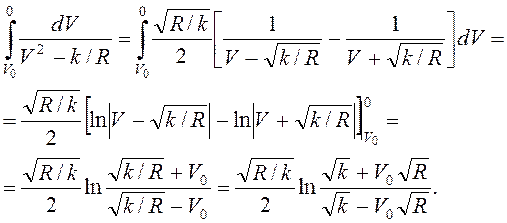
Тогда из (3.6) следует 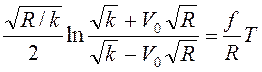 , или
, или 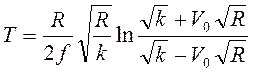 .
.
Ответ: 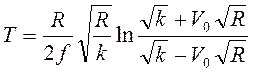 .
.
3. Запишем второй закон Ньютона для точки (рис. 3.4)
![]() .
.
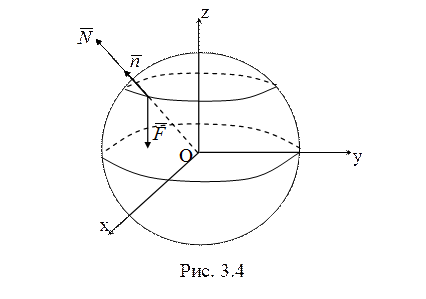 В проекциях на оси координат в совокупности
с уравнением связи, в качестве которого выступает уравнение сферы, он дает
систему уравнений
В проекциях на оси координат в совокупности
с уравнением связи, в качестве которого выступает уравнение сферы, он дает
систему уравнений
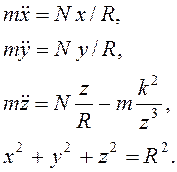 (3.7)
(3.7)
Дифференцированием по времени уравнения
связи получим ![]() , и далее
, и далее ![]() , или
, или ![]() . Умножением
первых уравнений системы (3.7) на
. Умножением
первых уравнений системы (3.7) на ![]() соответственно и их последующим
сложением получаем
соответственно и их последующим
сложением получаем
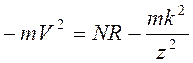 .
.
Так как работу совершает
только консервативная стационарная сила ![]() , то выполнен
закон сохранения полной механической энергии точки
, то выполнен
закон сохранения полной механической энергии точки
![]() .
.
Кинетическая энергия 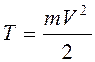 , для потенциальной энергии
, для потенциальной энергии 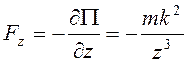 , т.е.
, т.е. 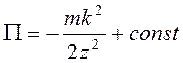 . Тогда
. Тогда
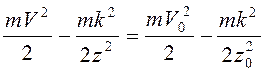 ,
т.е.
,
т.е. 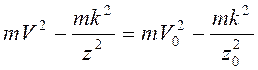 ,
,
и 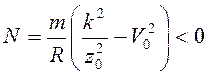 (сила
реакции направлена внутрь сферы, а точка удерживается на сфере за счет достаточно
большой начальной скорости).
(сила
реакции направлена внутрь сферы, а точка удерживается на сфере за счет достаточно
большой начальной скорости).
Подстановкой значения ![]() в уравнения (3.7) получим вместе с начальными
условиями
в уравнения (3.7) получим вместе с начальными
условиями
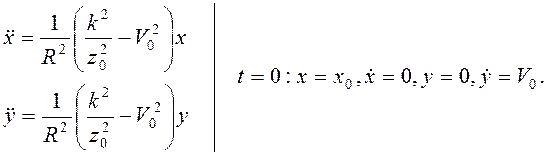
Если 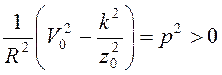 , то
решение последней системы дифференциальных уравнений при заданных начальных
условиях имеет вид
, то
решение последней системы дифференциальных уравнений при заданных начальных
условиях имеет вид
 .
.
Так как ![]() , то
, то 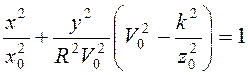 , и проекцией траектории
, и проекцией траектории
точки на плоскость ![]() будет эллипс, задаваемый последним
уравнением. Траекторией точки будет линия пересечения сферы и эллиптического
цилиндра, в основании которого лежит указанный эллипс, а осью цилиндра является
ось
будет эллипс, задаваемый последним
уравнением. Траекторией точки будет линия пересечения сферы и эллиптического
цилиндра, в основании которого лежит указанный эллипс, а осью цилиндра является
ось ![]() .
.
Ответ: 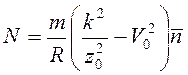 , эллипс
, эллипс 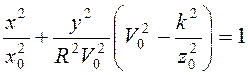 .
.
4.Второй закон Ньютона в проекциях на касательную и нормаль к траектории точки (рис. 3.5) принимает вид
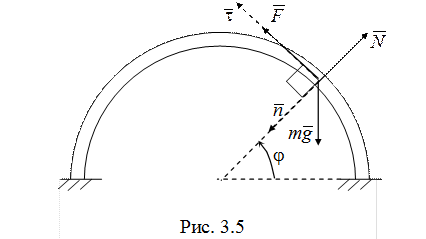
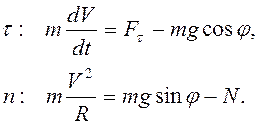
При отсутствии давления ![]()
![]() . Дифференцируя последнее равенство по
времени, получим
. Дифференцируя последнее равенство по
времени, получим 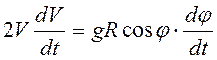 . Так как при движении по
окружности
. Так как при движении по
окружности 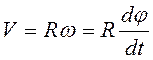 , то
, то 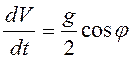 , и,
следовательно,
, и,
следовательно, 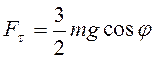 .
.
Ответ: 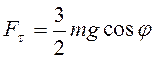 .
.
5. Силы, действующие на груз, показаны на рис. 3.6.
Второй закон Ньютона в проекции на оси ![]() и
и ![]() дает уравнения
дает уравнения
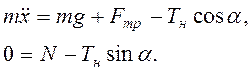 (3.8)
(3.8)
Геометрически 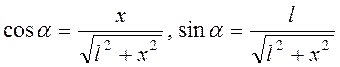 .
Реакция
.
Реакция 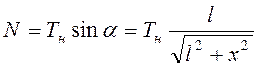 , сила трения
, сила трения 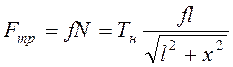 .
.
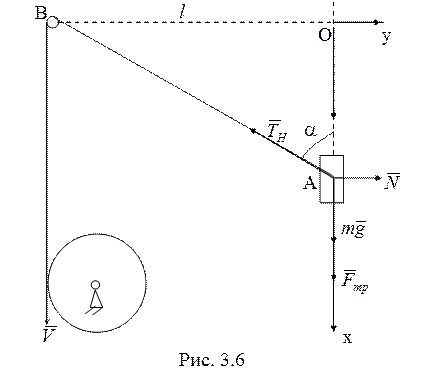 Длина нити АВ
уменьшается с постоянной скоростью
Длина нити АВ
уменьшается с постоянной скоростью ![]() ,то есть
,то есть
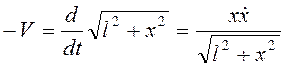 .
.
Отсюда 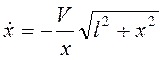 .
Дифференцированием по времени получим
.
Дифференцированием по времени получим 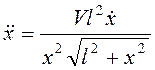 , а
учитывая выражение для
, а
учитывая выражение для ![]() :
: 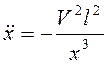 .
.
Тогда из первого уравнения системы (3.8) получим для натяжения нити
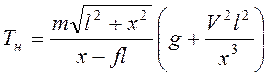 .
.
Ответ: 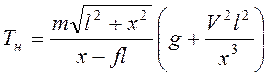 .
.
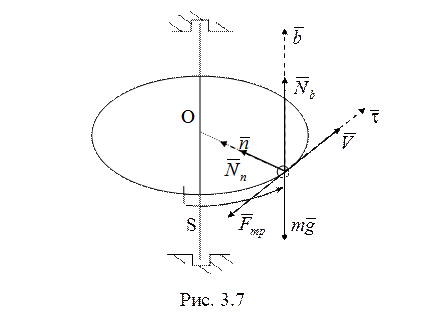 6. Силы, действующие
на материальную точку, показаны на рис. 3.7. Второй закон Ньютона в проекции на
оси траекторной системы координат (касательную, нормаль и бинормаль) даст следующую
систему уравнений
6. Силы, действующие
на материальную точку, показаны на рис. 3.7. Второй закон Ньютона в проекции на
оси траекторной системы координат (касательную, нормаль и бинормаль) даст следующую
систему уравнений
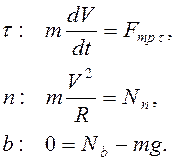
Так как сила трения
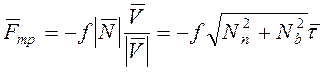 , то
, то 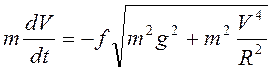 , или
, или
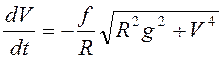 .
.
Если ![]() - путь,
пройденный точкой от начального до конечного положения, то
- путь,
пройденный точкой от начального до конечного положения, то
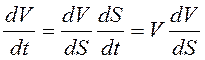 ,
и
,
и 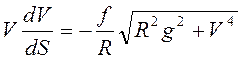 .
.
Разделением переменных получим
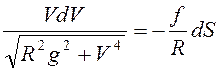 ,
,
а интегрированием при совершении точкой полного оборота по кольцу имеем
![]()
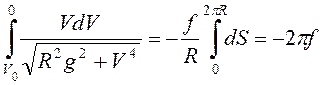 .
.
Интеграл в левой части вычисляем с
использованием замены ![]() :
:
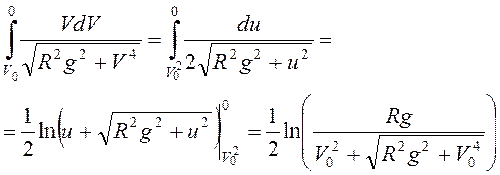 ,
,
то есть 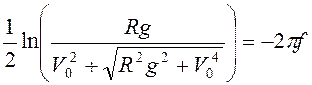 .
.
Отсюда следует, что ![]() , т.е. должно быть
, т.е. должно быть ![]() .
.
Возведением в квадрат и последующим вычислением получим
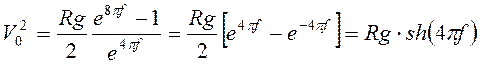 .
.
Ответ: ![]() .
.
7. 1-й способ. Рассмотрим движение стержня в воде (рис. 3.8). Сила тяжести и архимедова сила приводятся к центру масс стержня С. Тогда по теореме о движении центра масс стержня
![]() .
.
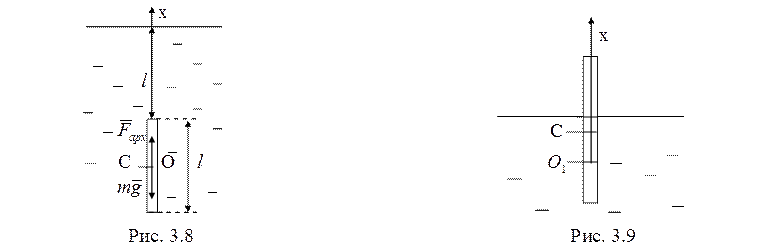 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.