 33. Силы, действующие
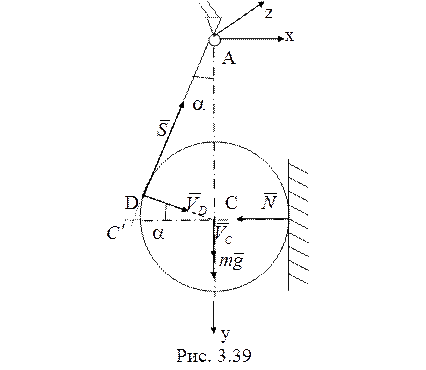
на диск, показаны на рис. 3.39. Работу совершает только сила тяжести диска. По
теореме об изменении кинетической энергии
33. Силы, действующие
на диск, показаны на рис. 3.39. Работу совершает только сила тяжести диска. По
теореме об изменении кинетической энергии ![]() . Кинетическая
энергия диска при плоскопараллельном движении
. Кинетическая
энергия диска при плоскопараллельном движении
![]() .
.
Момент инерции диска ![]() .
.
Так как мгновенный центр скоростей
диска расположен в точке ![]() , то угловая скорость
, то угловая скорость ![]() ,
,
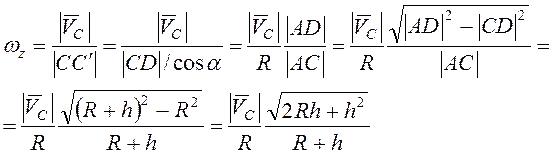 .
.
Тогда кинетическая энергия диска 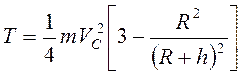 .
.
Работа силы тяжести ![]() , поэтому из теоремы об изменении кинетической
энергии следует
, поэтому из теоремы об изменении кинетической
энергии следует
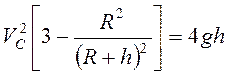 . (3.47)
. (3.47)
Дифференцируя (3.47) по времени и
учитывая, что ![]() , получим
, получим
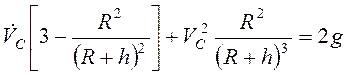 .
.
Учитывая (3.47) найдем составляющую ускорения
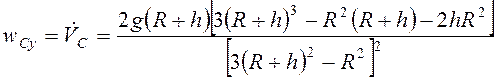 .
.
По теореме о движении центра масс диска
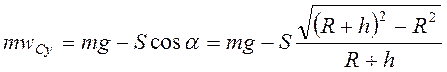 .
.
Отсюда натяжение нити
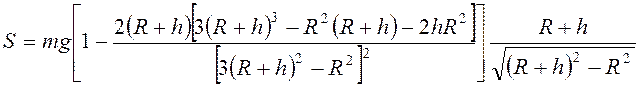 .
.
Ответ: 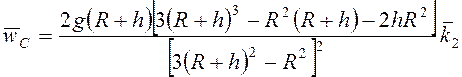 ,
,
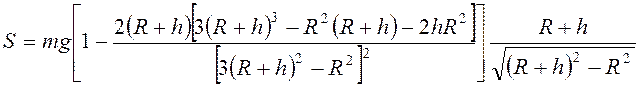 .
.
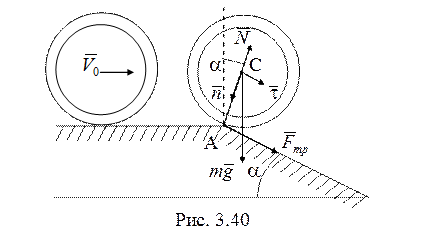
34. Переход обруча на
наклонную плоскость показан на рис. 3.40. Условия отрыва и отсутствия
проскальзывания состоит в том, что нормальная реакция опоры ![]() , а составляющая силы трения
, а составляющая силы трения ![]() . Обруч при этом переходе вращается около
неподвижной точки А.
. Обруч при этом переходе вращается около
неподвижной точки А.
 По теореме о движении
центра масс в проекции на касательную и нормаль к его траектории
По теореме о движении
центра масс в проекции на касательную и нормаль к его траектории
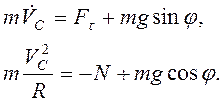 (3.48)
(3.48)
Силы реакции опоры и трения выразим
через параметры движения используя теорему об изменении кинетической энергии ![]() . При вращательном движении
. При вращательном движении ![]() . Момент инерции
. Момент инерции ![]() ,
угловая скорость
,
угловая скорость ![]() , и кинетическая энергия
, и кинетическая энергия ![]() . Работа силы тяжести
. Работа силы тяжести ![]() .
.
Тогда из теоремы об изменении кинетической энергии следует
![]() . (3.49)
. (3.49)
Из второго уравнения системы (3.48) получим для нормальной реакции опоры
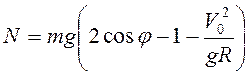 .
.
При отсутствии отрыва ![]() при всех углах
при всех углах ![]() , т.е.
достаточно потребовать
, т.е.
достаточно потребовать ![]() , или
, или 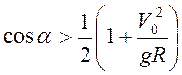 .
.
Дифференцируя по времени
(3.49) получим ![]() . Так как
. Так как ![]() ,
то
,
то 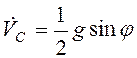 , и из первого уравнения системы (3.48)
касательная составляющая силы трения
, и из первого уравнения системы (3.48)
касательная составляющая силы трения 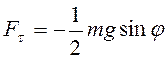 . Условие
. Условие ![]() ведет к неравенству
ведет к неравенству 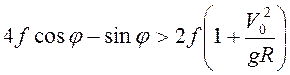 , которое должно выполняться при
, которое должно выполняться при ![]() .
.
Рассматривая левую часть
неравенства ![]() , найдем
, найдем ![]() , т.е.
, т.е. ![]() убывает, и выполнения указанного неравенства
достаточно потребовать при
убывает, и выполнения указанного неравенства
достаточно потребовать при ![]() . Отсюда
. Отсюда 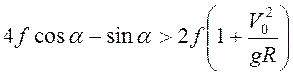 .
.
Ответ: 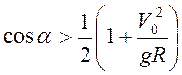 ,
, 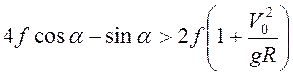 .
.
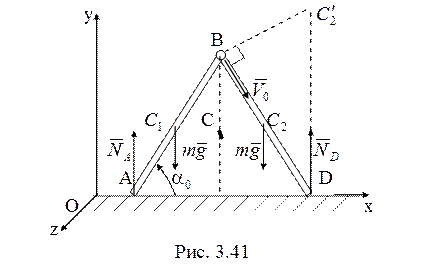 35. 1-й способ. Рассматриваемая система имеет две
степени свободы. В качестве параметров, характеризующих ее положение (рис.
3.41) возьмем
35. 1-й способ. Рассматриваемая система имеет две
степени свободы. В качестве параметров, характеризующих ее положение (рис.
3.41) возьмем ![]() ,
, ![]() .
.
Внешние силы, действующие
на систему, вертикальны. Составляющая их главного вектора 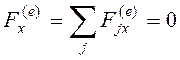 , и, следовательно, составляющая импульса системы
, и, следовательно, составляющая импульса системы
![]() . Центр масс системы С расположен на одной
вертикали с точкой В, и
. Центр масс системы С расположен на одной
вертикали с точкой В, и ![]() , т.е.
, т.е.
![]() . (3.50)
. (3.50)
Второе уравнение, характеризующее движение системы, найдем с помощью теоремы об изменении кинетической энергии. Так как работу совершают только консервативные стационарные силы тяжести, то следствием указанной теоремы является закон сохранения полной механической энергии системы
![]() .
.
Кинетическая энергия системы
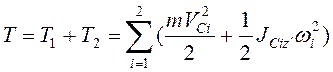 . (3.51)
. (3.51)
Координаты центров масс стержней 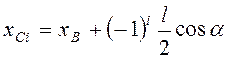 ,
, 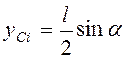 ;
составляющие скорости
;
составляющие скорости 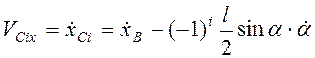 ,
, 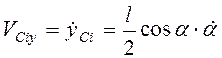 . Моменты инерции
. Моменты инерции 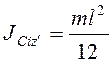 ,
составляющие угловых скоростей
,
составляющие угловых скоростей ![]() . Подстановка последних
формул в (3.51) даст
. Подстановка последних
формул в (3.51) даст ![]() .
.
Потенциальная энергия
системы 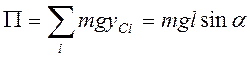 . В начальный момент времени
. В начальный момент времени 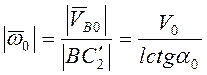 . Учитывая (3.50), закон сохранения механической
энергии системы даст
. Учитывая (3.50), закон сохранения механической
энергии системы даст
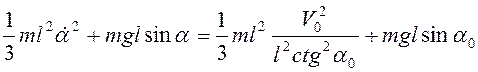 .
.
Поэтому в момент падения стержней при
![]()
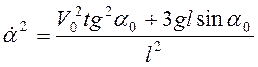 ;
; 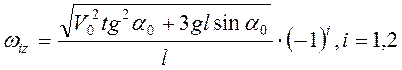 .
.
Составляющие скорости точки В
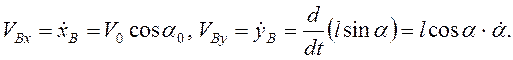
В момент падения при ![]()
![]() .
.
2-й способ. Так как ![]() (см.
предыдущий способ), то поступательно движущаяся вместе с точкой В вправо
система координат
(см.
предыдущий способ), то поступательно движущаяся вместе с точкой В вправо
система координат ![]() (рис. 3.42) будет инерциальной,
и в ней также
(рис. 3.42) будет инерциальной,
и в ней также ![]() .
.
 Кинетическая энергия
стержней
Кинетическая энергия
стержней 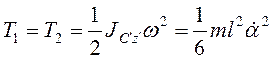 , потенциальная энергия
, потенциальная энергия
![]() .
.
Начальная угловая скорость стержней
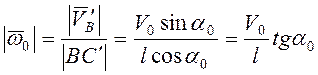 .
.
Дальнейшие вычисления повторяют первый способ.
Ответ: 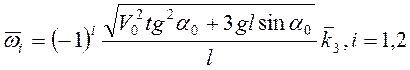 ,
,
![]() .
.
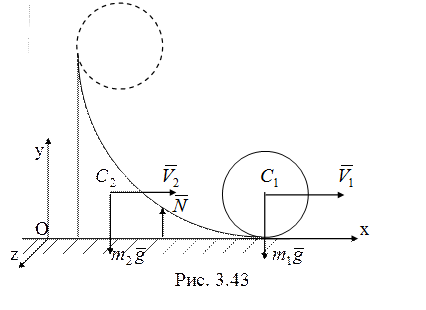 36. Рассмотрим
движение системы до достижения осью цилиндра крайнего нижнего положения (рис.
3.43). Внешние силы вертикальны, их составляющая
36. Рассмотрим
движение системы до достижения осью цилиндра крайнего нижнего положения (рис.
3.43). Внешние силы вертикальны, их составляющая ![]() , и
составляющая импульса системы
, и
составляющая импульса системы
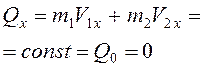 . (3.52)
. (3.52)
Изменение кинетической
энергии системы равно работе силы тяжести цилиндра ![]() . Кинетическая
энергия системы в показанный на рис. 3.43 момент времени
. Кинетическая
энергия системы в показанный на рис. 3.43 момент времени ![]() . Угловая скорость цилиндра за счет
разности скоростей
. Угловая скорость цилиндра за счет
разности скоростей ![]() и
и ![]()
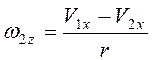 , момент инерции
, момент инерции ![]() .
Поэтому
.
Поэтому ![]() . Так как
. Так как ![]() (в начальный
момент времени система покоилась), то
(в начальный
момент времени система покоилась), то
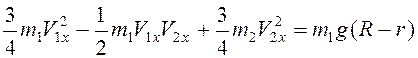 . (3.53)
. (3.53)
Совместным решением (3.52) и (3.53)
относительно неизвестных ![]() и
и ![]() получим
получим 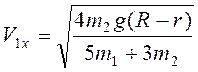 .
.
Ответ: 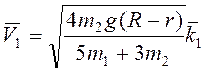 .
.
37. Работу в
рассматриваемой системе (рис. 3.44) совершают только силы взаимодействия между
точкой и платформой. Она равна изменению кинетической энергии системы ![]() .
.
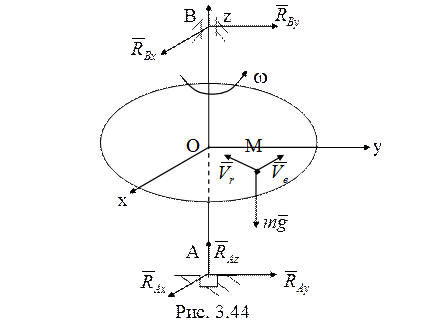 В начальный момент
времени
В начальный момент
времени ![]() . Скорость точки по теореме сложения скоростей
. Скорость точки по теореме сложения скоростей
![]() ,т.е.
,т.е.![]() ,
, ![]() .
.
В момент попадания точки на ось
вращения
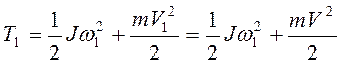 , и
, и
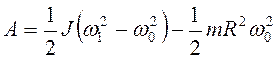 . (3.54)
. (3.54)
Чтобы найти угловую
скорость платформы в момент попадания точки на ось вращения воспользуемся
теоремой об изменении кинетического момента системы относительно оси вращения ![]() . Главный момент внешних сил тяжести и
реакции подшипников
. Главный момент внешних сил тяжести и
реакции подшипников ![]() , и поэтому
, и поэтому
![]() .
.
В начальный момент времени ![]() , в момент попадания точки на ось вращения
, в момент попадания точки на ось вращения ![]() , поэтому
, поэтому ![]() . Подставляя
последний результат в (3.54), получим
. Подставляя
последний результат в (3.54), получим 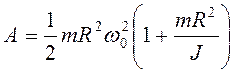 .
.
Ответ: 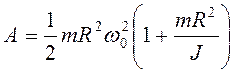 .
.
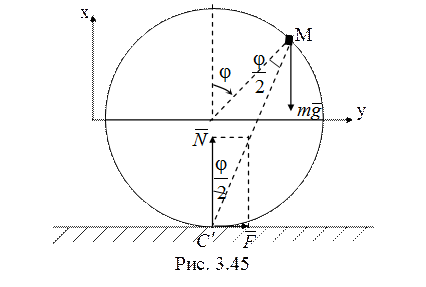 38. Рассмотрим
качение обруча по горизонтальной плоскости без проскальзывания до отрыва от нее
(рис. 3.45). Работу при этом совершает только сила тяжести и выполняется закон
сохранения полной механической энергии
38. Рассмотрим
качение обруча по горизонтальной плоскости без проскальзывания до отрыва от нее
(рис. 3.45). Работу при этом совершает только сила тяжести и выполняется закон
сохранения полной механической энергии
![]() .
.
Кинетическая энергия материальной точки,
принадлежащей катящемуся без проскальзывания обручу ![]() .
.
Скорость
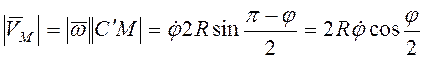 , и
, и
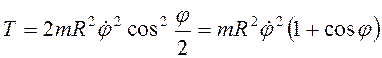 .
.
Потенциальная энергия ![]() , поэтому
, поэтому
![]() ,
то есть
,
то есть
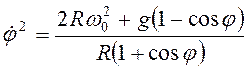 . (3.55)
. (3.55)
Отрыва обруча от
горизонтальной плоскости происходит в тот момент времени, когда обращается в
ноль нормальная реакция плоскости ![]() . По теореме о движении
центра масс в проекции на ось
. По теореме о движении
центра масс в проекции на ось ![]()
![]() . (3.56)
. (3.56)
Так как ![]() , то
, то ![]() . Дифференцируя по времени (3.55) после
некоторых преобразований получим
. Дифференцируя по времени (3.55) после
некоторых преобразований получим 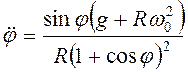 . Далее из (3.56)
найдем, что
. Далее из (3.56)
найдем, что ![]() . Отрыв обруча от плоскости произойдет при
значении угла
. Отрыв обруча от плоскости произойдет при
значении угла ![]() :
: ![]() .
.
Заметим, что так как вся
масса системы сосредоточена в точке М, то вследствие принципа Д’Аламбера
равнодействующая силы трения ![]() и нормальной реакции
опоры
и нормальной реакции
опоры ![]() направлена по прямой СМ, и сила трения
направлена по прямой СМ, и сила трения ![]() обращается в ноль одновременно с
обращается в ноль одновременно с ![]() . В этом также можно убедиться, вычислив
силу трения. Действительно
. В этом также можно убедиться, вычислив
силу трения. Действительно ![]() ,
, ![]() ,
, ![]() и
и
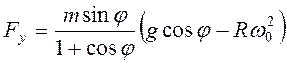 .
.
Условие качения без
проскальзывания состоит в выполнении неравенства ![]() , т.е.
(см. рис. 3.45)
, т.е.
(см. рис. 3.45) ![]() . Этого достаточно потребовать
при угле
. Этого достаточно потребовать
при угле ![]() . Так как
. Так как 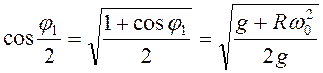 ,
, 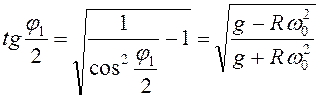 , то
, то 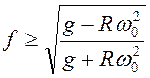 .
.
Ответ: 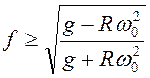 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.