12. Внешние силы,
действующие на систему, векторы которых лежат в плоскости диска, отсутствуют.
Так как в начальный момент времени система покоилась, то центр масс системы и в
дальнейшем будет оставаться неподвижным. При равенстве масс точки и диска он
расположен по середине отрезка ![]() (рис. 3.15). На рис.
3.15 показаны начальное и текущее положение системы.
(рис. 3.15). На рис.
3.15 показаны начальное и текущее положение системы.
 По теореме о
сохранении количества движения системы
По теореме о
сохранении количества движения системы
![]() . (3.15)
. (3.15)
Так как ![]() ,
, ![]() , то в проекции на касательную к траектории
центра масс диска
, то в проекции на касательную к траектории
центра масс диска ![]() из (3.15) следует
из (3.15) следует
![]() (
(![]() - угловая скорость диска). (3.16)
- угловая скорость диска). (3.16)
Главный момент внешних
сил относительно оси ![]() , перпендикулярной плоскости
диска,
, перпендикулярной плоскости
диска, ![]() , т.е. кинетический момент первоначально
покоящейся системы
, т.е. кинетический момент первоначально
покоящейся системы ![]() , или
, или
![]() . (3.17)
. (3.17)
Отсюда следует после подстановки в
(3.17) необходимых величин и преобразований, что 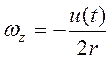 . Тогда
из (3.16) следует, что
. Тогда
из (3.16) следует, что 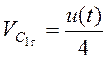 .
.
Ответ: 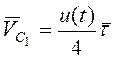 .
.
13. Силы, действующие на
тела, показаны на рис. 3.16. Воспользуемся теоремой об изменении кинетического
момента для каждого тела относительно оси, проходящей перпендикулярно плоскости
движения "от нас", и через мгновенный центр скоростей каждого тела ![]() (точку касания с горизонтальной плоскостью
качения). Тогда из составляемых уравнений будут исключены не подлежащие
(точку касания с горизонтальной плоскостью
качения). Тогда из составляемых уравнений будут исключены не подлежащие
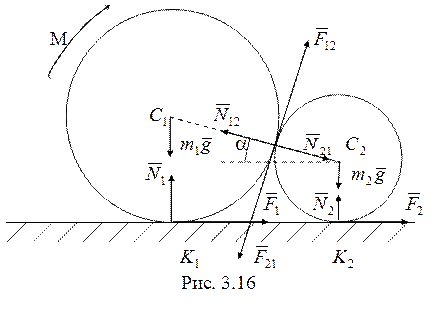 |
Согласно указанной теореме 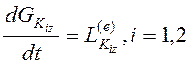 . Так как
. Так как 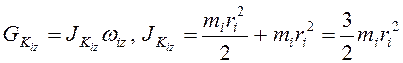 , то
, то
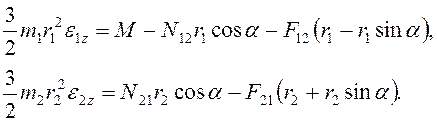 (3.18)
(3.18)
В силу третьего закона Ньютона ![]() , при проскальзывании катков друг
относительно друга сила трения
, при проскальзывании катков друг
относительно друга сила трения ![]() . Если
. Если ![]() - горизонтальная ось, то в отсутствие
отрыва катков друг от друга
- горизонтальная ось, то в отсутствие
отрыва катков друг от друга ![]() , т.е.
, т.е. ![]() , или
, или ![]() . Дифференцированием
получаем, что
. Дифференцированием
получаем, что ![]() .
.
Если ![]() ,
, ![]() , то
, то
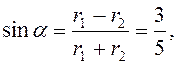
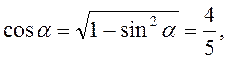
![]() , и решением системы (3.18) получим
, и решением системы (3.18) получим 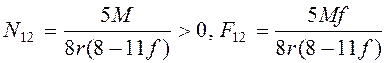 .
.
Из теоремы о движении
центра масс первого катка в проекции на вертикаль ![]() .
.
Отсюда 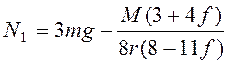 . При
отсутствии отрыва катка от плоскости
. При
отсутствии отрыва катка от плоскости ![]() , или
, или 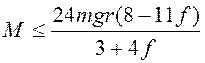 .
.
Замечание. При ![]() система
будет оставаться в равновесии, что можно показать решением соответствующей
задачи статики для рассматриваемой системы.
система
будет оставаться в равновесии, что можно показать решением соответствующей
задачи статики для рассматриваемой системы.
Ответ: 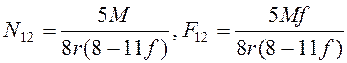 ,
, 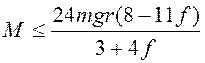 .
.
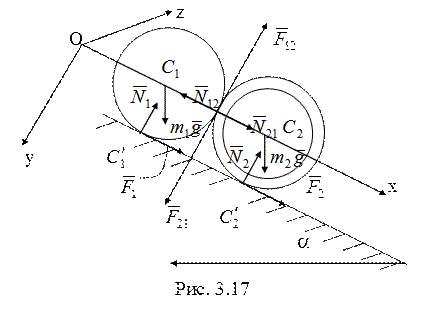 14. Силы, действующие
на тела, показаны на рис. 3.17. Для составления уравнений движения тел
воспользуемся теоремой об изменении кинетического момента каждого тела
относительно оси
14. Силы, действующие
на тела, показаны на рис. 3.17. Для составления уравнений движения тел
воспользуемся теоремой об изменении кинетического момента каждого тела
относительно оси ![]() , проходящей через мгновенный
центр скоростей тела
, проходящей через мгновенный
центр скоростей тела
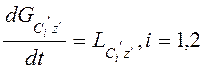 .
.
Так как ![]() , то
, то
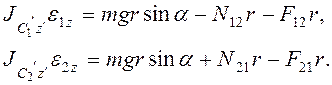 (3.19)
(3.19)
В соответствии с теоремой Штейнера ![]() ,
, ![]() , из
третьего закона Ньютона
, из
третьего закона Ньютона ![]() , силы трения при
проскальзывании цилиндров друг относительно друга
, силы трения при
проскальзывании цилиндров друг относительно друга ![]() .
.
Координаты ![]() , т.е.
, т.е. ![]() , и
ускорения центров цилиндров одинаковы. Угловые ускорения
, и
ускорения центров цилиндров одинаковы. Угловые ускорения 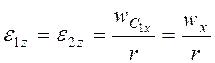 . Тогда из (3.19) следует
. Тогда из (3.19) следует
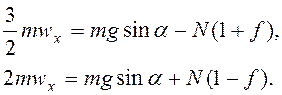
Решением последней линейной системы
находим 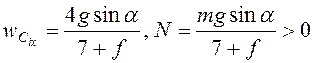 .
.
По теореме о движении
центров масс каждого тела ![]() , т.е. в проекции на
оси
, т.е. в проекции на
оси ![]() и
и ![]()
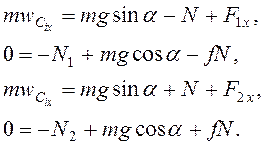
Решением последней системы получим
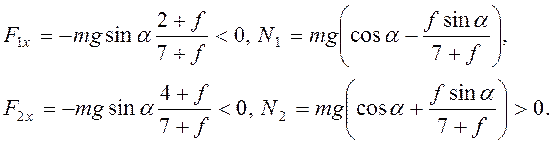
При отсутствии отрыва цилиндра от плоскости
должно быть ![]() , т.е.
, т.е.
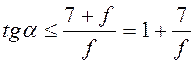 . (3.20)
. (3.20)
При отсутствии проскальзывании
цилиндров по плоскости силы трения ![]() . Отсюда следует, что
должно быть
. Отсюда следует, что
должно быть
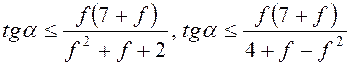 . (3.21)
. (3.21)
Так как 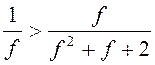 , то
условие (3.20) выполнено при выполнении условий (3.21), и его можно опустить. При
, то
условие (3.20) выполнено при выполнении условий (3.21), и его можно опустить. При
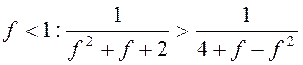 , и достаточно выполнить условие
, и достаточно выполнить условие 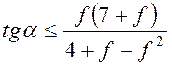 (при увеличении угла
(при увеличении угла ![]() первым начнет проскальзывать нижний
цилиндр).
первым начнет проскальзывать нижний
цилиндр).
Ответ: 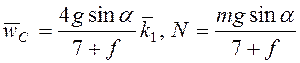 ,
, 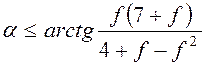 .
.
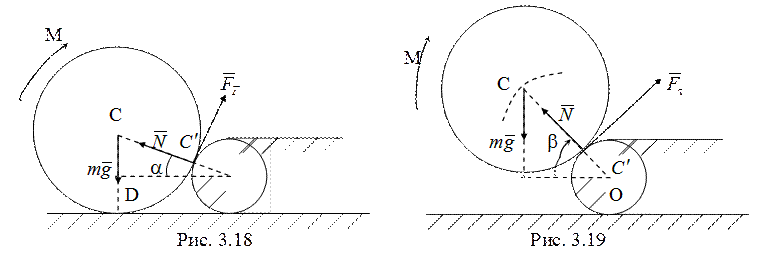
15. Чтобы момента ![]() было достаточно для отрыва цилиндра от
горизонтальной плоскости нужно, чтобы главный момент сил, показанных на рис.
3.18, относительно оси
было достаточно для отрыва цилиндра от
горизонтальной плоскости нужно, чтобы главный момент сил, показанных на рис.
3.18, относительно оси ![]() , направленной "от нас"
перпендикулярно плоскости рисунка, был положителен, т.е.
, направленной "от нас"
перпендикулярно плоскости рисунка, был положителен, т.е. ![]() . Так как
. Так как 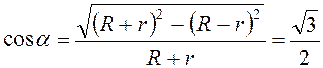 ,
, 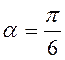 , то
, то
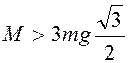 . (3.22)
. (3.22)
 |
Рассмотрим вкатывание
цилиндра на выступ в отсутствии проскальзывания (рис. 3.19). Для составления
уравнения, описывающего движение цилиндра, воспользуемся теоремой об изменении
кинетического момента относительно оси ![]() , проходящей
через мгновенный центр скоростей
, проходящей
через мгновенный центр скоростей
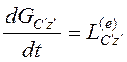 .
.
Так как ![]() ,
момент инерции
,
момент инерции 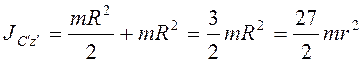 , то
, то
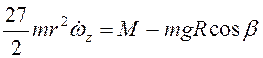 .
.
Центр масс цилиндра С движется по
окружности радиуса ![]() , его скорость
, его скорость ![]() , т.е.
, т.е. ![]() ,
поэтому
,
поэтому ![]() . Так как
. Так как 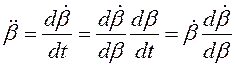 ,
то
,
то 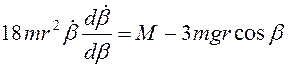 . Разделяя переменные и интегрируя, получим
. Разделяя переменные и интегрируя, получим
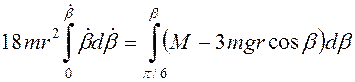 , или
, или
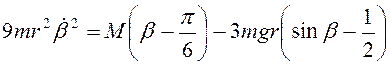 .
.
Для установления условия
вкатывания без проскальзывания нужно найти силу трения ![]() и
нормальную реакцию выступа
и
нормальную реакцию выступа ![]() . Из теоремы о движении
центра масс цилиндра в проекциях на касательную и нормаль к траектории этой точки
. Из теоремы о движении
центра масс цилиндра в проекциях на касательную и нормаль к траектории этой точки
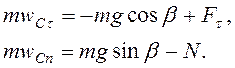
Так как ![]() , то
, то
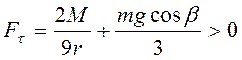 ,
,
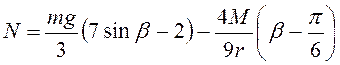 .
.
При ![]() при отсутствии отрыва должно быть
при отсутствии отрыва должно быть ![]() .
. ![]() Производная
Производная
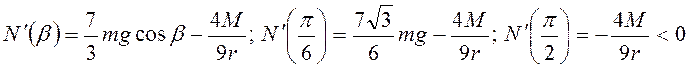 .
.
Если ![]() , то на
указанном интервале измерения угла
, то на
указанном интервале измерения угла ![]()
![]() монотонно
убывает, и для выполнения условия
монотонно
убывает, и для выполнения условия ![]() достаточно потребовать
достаточно потребовать ![]() . Тогда
. Тогда
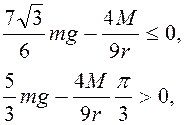 т.е.
т.е. 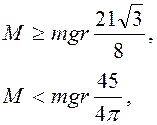
что одновременно невозможно.
Если же ![]() , то
, то ![]() сначала
возрастает, а затем убывает. Для выполнения условия
сначала
возрастает, а затем убывает. Для выполнения условия ![]() нужно
потребовать
нужно
потребовать ![]() , т.е.
, т.е. 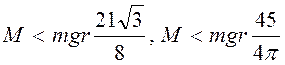 . Первое
из последних двух неравенств выполняется при выполнении второго, т.е.
достаточно выполнить условие
. Первое
из последних двух неравенств выполняется при выполнении второго, т.е.
достаточно выполнить условие
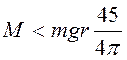 . (3.23)
. (3.23)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.