Условие отсутствия
проскальзывания дает неравенство ![]() , т.е.
, т.е.
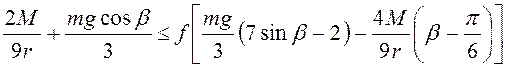 . (3.24)
. (3.24)
Левая часть неравенства монотонно
убывает при изменении угла ![]() , правая часть сперва
возрастает, а затем убывает. Необходимым условием выполнения (3.24) является
его выполнение при
, правая часть сперва
возрастает, а затем убывает. Необходимым условием выполнения (3.24) является
его выполнение при ![]() и при
и при ![]() т.е.
т.е.
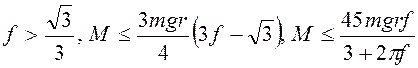 (3.25)
(3.25)
Ответ: 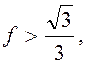
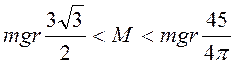 ,
, 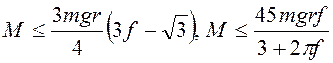 .
.
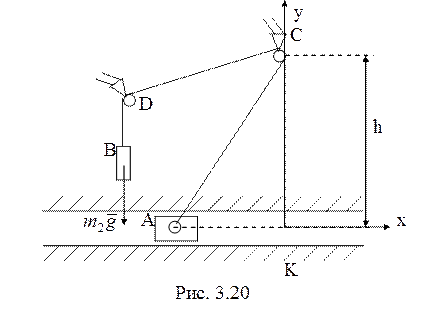
16. Работу в
рассматриваемой системе (рис. 3.20) совершает только консервативная
стационарная сила тяжести ![]() , поэтому выполняется
закон сохранения полной механической энергии
, поэтому выполняется
закон сохранения полной механической энергии
![]() . (3.26)
. (3.26)
Кинетическая энергия системы 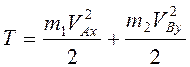 . Уравнение связи дает условие постоянства
длины нити
. Уравнение связи дает условие постоянства
длины нити ![]() . При введенной системе координат оно
примет вид
. При введенной системе координат оно
примет вид
![]() .
.
Дифференцированием по времени получим
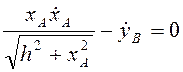 , т.е.
, т.е. 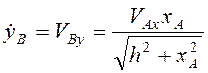 , и
, и 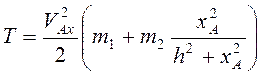
Потенциальная энергия системы
![]() .
.
Подставляя полученное выражение в (3.26) имеем для момента попадания точки А в точку К
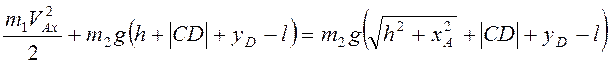 ,
,
откуда находим 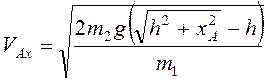 .
.
Ответ: 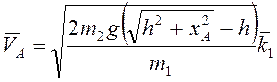 .
.
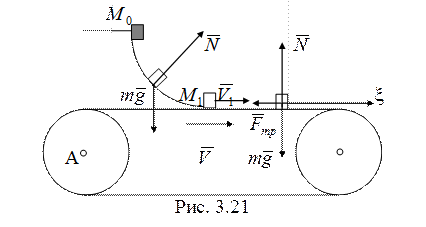 17. Рассмотрим движение груза до
попадания на ленту (рис. 3.21). Работу при этом совершает сила тяжести груза.
По теореме об изменении кинетической энергии
17. Рассмотрим движение груза до
попадания на ленту (рис. 3.21). Работу при этом совершает сила тяжести груза.
По теореме об изменении кинетической энергии ![]() . Так
как
. Так
как ![]() , работа силы тяжести
, работа силы тяжести ![]() , то скорость в момент попадания груза на
ленту
, то скорость в момент попадания груза на
ленту ![]() .
.
Система отсчета связанная
с равномерно движущейся лентой, является инерциальной, и в ней вид теоремы об
изменении кинетической энергии идентичен: ![]() . Так
как
. Так
как ![]() ,
, ![]() ,
работа силы трения
,
работа силы трения 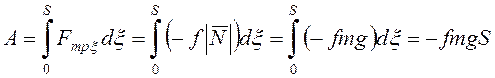 , то путь, пройденный грузом до
остановки относительно ленты
, то путь, пройденный грузом до
остановки относительно ленты 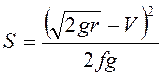 .
.
Ответ: 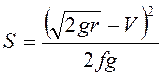 .
.
 |
К этому моменту времени по теореме об изменении кинетической энергии
![]() . (3.27)
. (3.27)
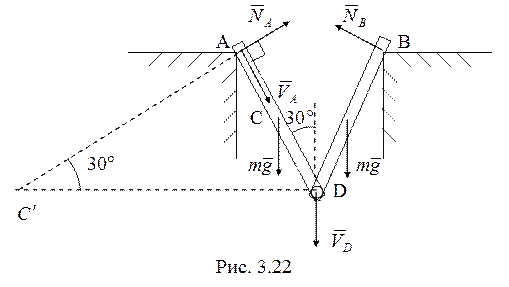
Кинетическую энергию
системы выразим через скорость точки D. Скорость точки D
направлена по вертикали вниз, скорость точки А направлена по касательной
поверхности между стержнем и опорой (из условия непроницания стержня сквозь
опору), т.е. вдоль стрежня. Тогда мгновенный центр скоростей стержня АВ
расположен в точке ![]() . Кинетическая энергия системы
. Кинетическая энергия системы
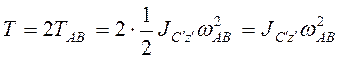 .
.
По теореме Штейнера ![]() . Так как
. Так как 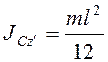 , и
, и 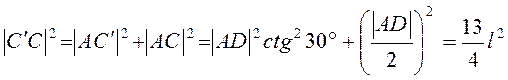 , то
, то 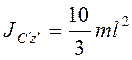 . Угловая
скорость стержня
. Угловая
скорость стержня 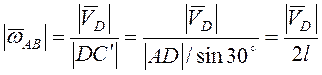 , и
, и 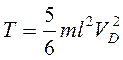 .
.
Работа силы тяжести к рассматриваемому моменту времени
![]() .
.
Подстановка найденных выражений в
(3.27) даст 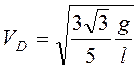 .
.
Ответ: 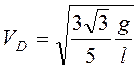 .
.
 19. По теореме об
изменении кинетической энергии
19. По теореме об
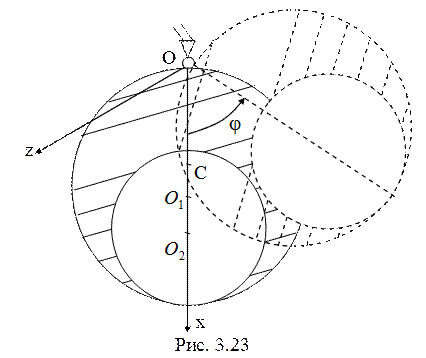
изменении кинетической энергии ![]() . В текущем положении
(рис. 3.23)
. В текущем положении
(рис. 3.23) ![]() . Момент инерции
. Момент инерции 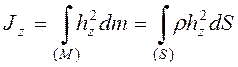 (
(![]() - площадь пластины,
- площадь пластины, ![]() - плотность).
- плотность).
Разбивая площадь интегрирования на площадь диска без выреза ![]() и площадь выреза
и площадь выреза ![]() получим
получим
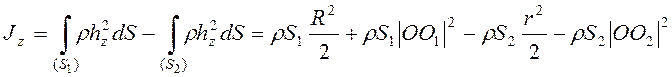 .
.
Так как ![]() , то
, то 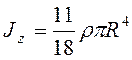 ,
,
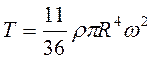 .
.
Работа силы тяжести ![]() . Расстояние до центра тяжести пластины
. Расстояние до центра тяжести пластины 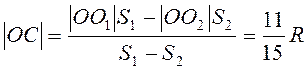 . Масса пластины
. Масса пластины 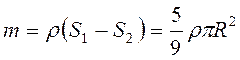 .
Тогда
.
Тогда 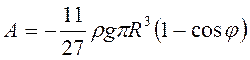 .
.
1) При максимальном
отклонении пластины на угол ![]()
![]() ,
т.е.
,
т.е.
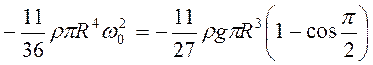 , или
, или 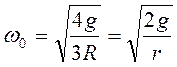 .
.
2) При ![]() ,
, ![]() ,
,
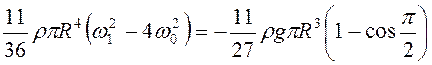 , т.е.
, т.е. 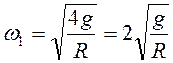 .
.
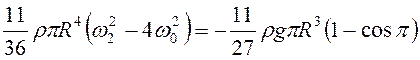 , т.е.
, т.е. 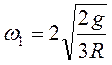 .
.
Ответ: 1) 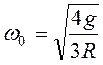 ; 2)
; 2) 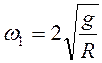 ,
, 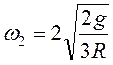 .
.
20. При рассматриваемом
качении системы без проскальзывания (рис. 3.24) работа силы реакции опоры ![]() и силы трения
и силы трения ![]() равна
нулю, и работу совершает только сила тяжести системы. По теореме об изменении
кинетической энергии системы на рассматриваемом интервале времени
равна
нулю, и работу совершает только сила тяжести системы. По теореме об изменении
кинетической энергии системы на рассматриваемом интервале времени
![]() . (3.28)
. (3.28)
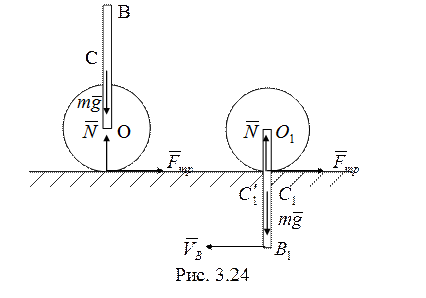 Кинетическая энергия
Кинетическая энергия ![]()
![]() (
(![]() - точка касания диска и плоскости, она
является при качении без проскальзывания мгновенным центром скоростей системы).
Момент инерции системы стержень-диск
- точка касания диска и плоскости, она
является при качении без проскальзывания мгновенным центром скоростей системы).
Момент инерции системы стержень-диск
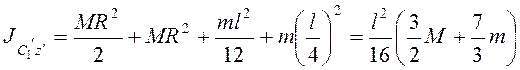 .
.
Угловая скорость 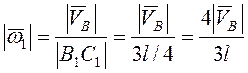 , и
, и 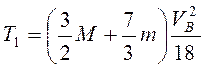 .
.
Работа силы тяжести ![]() (высота центра цилиндра не изменяется, и
сила тяжести цилиндра работу не совершает). Поэтому из (3.28) следует
(высота центра цилиндра не изменяется, и
сила тяжести цилиндра работу не совершает). Поэтому из (3.28) следует 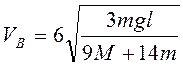 .
.
Ответ: 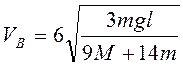 .
.
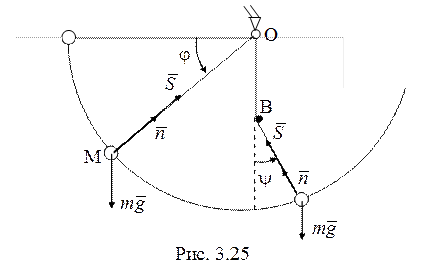 21. На участке
опускания нити из начального положения в вертикальное (рис. 3.25) натяжение
нити
21. На участке
опускания нити из начального положения в вертикальное (рис. 3.25) натяжение
нити ![]() может быть найдено из уравнения второго закона
Ньютона в проекции на нормаль к траектории точки М:
может быть найдено из уравнения второго закона
Ньютона в проекции на нормаль к траектории точки М: ![]() , или
, или
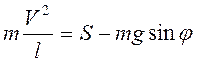 (
(![]() - длина нити).
- длина нити).
Скорость точки М найдем с
помощью теоремы об изменении кинетической энергии ![]() , или
, или
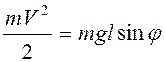 . (3.28)
. (3.28)
Тогда 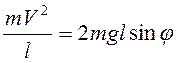 , и
натяжение
, и
натяжение ![]() . При
. При 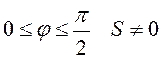 .
.
При абсолютно неупругом
ударе о гвоздь скорость точки В нити после удара станет нулевой, а из теоремы
об изменении кинетического момента для участка ВМ следует, что скорость точки М
за время удара не изменится. В крайнем нижнем положении при ![]() она, как следует из (3.28), будет равной
она, как следует из (3.28), будет равной ![]() .
.
После начала поворота нижней части маятника около точки В из второго закона Ньютона в проекции на нормаль к траектории точки М следует
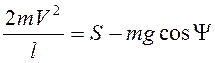 . (3.29)
. (3.29)
По теореме об изменении кинетической
энергии 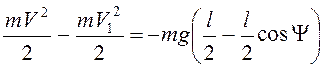 , т.е.
, т.е. 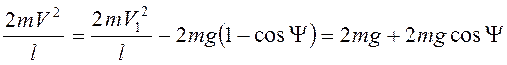 . Тогда
из (3.29) натяжение нити
. Тогда
из (3.29) натяжение нити ![]() .
. ![]() при
при ![]() , т.е.
при
, т.е.
при ![]() . После отклонения на этот угол подвижная
часть нити перестает быть прямолинейной.
. После отклонения на этот угол подвижная
часть нити перестает быть прямолинейной.
Ответ: ![]()
22. Для рассматриваемой
системы (рис. 3.26) по теореме об изменении кинетической энергии ![]() , или
, или ![]() , т.е.
, т.е. ![]() .
.
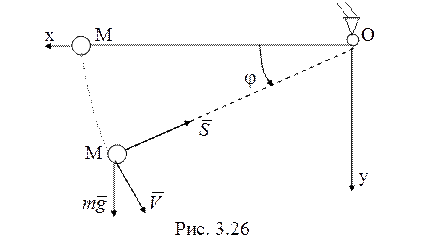 Вертикальная составляющая скорости
точки М
Вертикальная составляющая скорости
точки М
![]() .
.
Если ![]() , то
, то 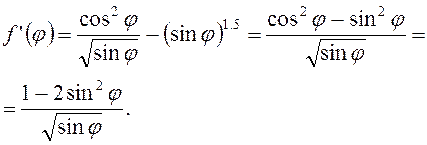 Тогда
Тогда ![]() при
при ![]() , т.е. при
, т.е. при ![]() . При
. При ![]() (функция возрастает), при
(функция возрастает), при ![]() (функция убывает). Максимальная
(функция убывает). Максимальная 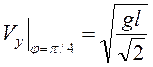 .
.
Ответ: ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.