После выхода верхнего конца стержня
из воды согласно теореме о движении центра масс в системе координат, показанной
на рис. 3.9, ![]() , где
, где ![]() . Тогда
. Тогда
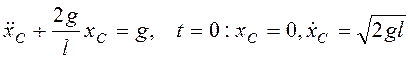 .
.
Общее решение линейного неоднородного
уравнения для ![]() имеет вид
имеет вид
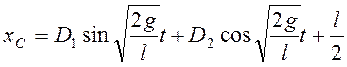 .
.
Из начальных условий следует, что
произвольные постоянные ![]() , и
, и
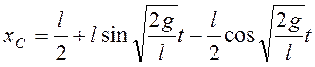 ,
,
т.е. центр масс стержня после выхода его из воды колеблется по вертикали около уровня поверхности воды. Максимальная высота подъема верхнего конца стержня над поверхностью воды
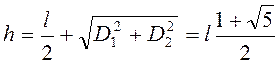 .
.
2-й способ. За время движения стержня в воде по
теореме об изменении кинетической энергии ![]() .
Кинетическая энергия поступательно движущегося стержня
.
Кинетическая энергия поступательно движущегося стержня ![]() ,
работа силы тяжести и архимедовой силы
,
работа силы тяжести и архимедовой силы ![]() ,
, ![]() . Тогда в момент касания верхним концом
стержня поверхности воды
. Тогда в момент касания верхним концом
стержня поверхности воды ![]() , и
, и ![]() .
.
После выхода верхнего
конца стержня из воды работа силы тяжести и архимедовой силы 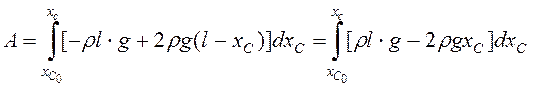 . В момент наибольшего выхода стержня из
воды скорость всех точек поступательно движущегося стержня будет нулевой, и по
теореме об изменении кинетической энергии
. В момент наибольшего выхода стержня из
воды скорость всех точек поступательно движущегося стержня будет нулевой, и по
теореме об изменении кинетической энергии
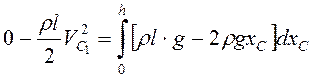 , т.е.
, т.е.![]() , или
, или ![]() .
.
Из последнего квадратного уравнения, оставляя наибольший его корень, имеем
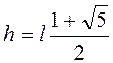 .
.
Вышеизложенное показывает, что второй способ дает результат, но не проясняет характера движения стержня.
Ответ: 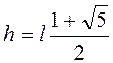 .
.
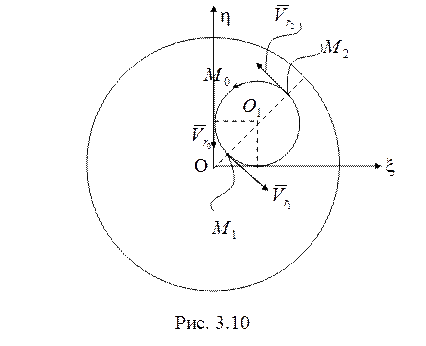 8. Рассмотрим движение точки относительно
диска. Вид сверху показан на рис. 3.10. Так как во все моменты времени
8. Рассмотрим движение точки относительно
диска. Вид сверху показан на рис. 3.10. Так как во все моменты времени ![]() , то
, то 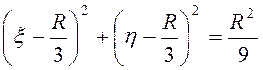 , т.е.
траекторией точки М относительно диска является окружность с центром в точке
, т.е.
траекторией точки М относительно диска является окружность с центром в точке ![]() и радиуса
и радиуса ![]() . Ближайшим
и наиболее удаленным от центра диска положениями точки М будут
. Ближайшим
и наиболее удаленным от центра диска положениями точки М будут ![]() и
и ![]() .
.
Составляющие относительной скорости точки М
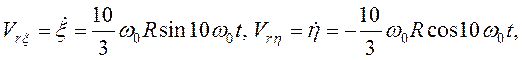
и 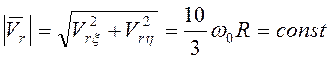 . В
соответствии с уравнениями относительного движения точки в положениях
. В
соответствии с уравнениями относительного движения точки в положениях ![]() и
и ![]() векторы
относительной скорости направлены по касательной к окружности, как показано на
рис. 3.10.
векторы
относительной скорости направлены по касательной к окружности, как показано на
рис. 3.10.
Сумма моментов внешних
сил, приложенных к системе, относительно оси ![]() , равна
нулю, поэтому как следствие теоремы об изменении кинетического момента
, равна
нулю, поэтому как следствие теоремы об изменении кинетического момента ![]() . Кинетический момент системы точка-диск
. Кинетический момент системы точка-диск
![]() .
.
Скорость точки М по теореме сложения
скоростей, учитывая вращательное движение диска, ![]() .
.
Для наиболее близкого к
центру диска положения ![]()
![]() . (3.9)
. (3.9)
В момент времени ![]() , соответствующий положению
, соответствующий положению ![]() ,
,
![]() .
.
Так как 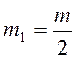 ,
, 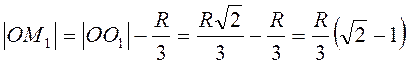 ,
, 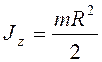 , то
, то
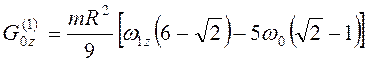 .
.
В начальный момент времени ![]() . Так как
. Так как 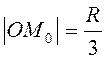 , то
, то 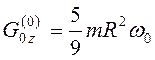 . Подставив найденные выражения в (3.9),
получим
. Подставив найденные выражения в (3.9),
получим 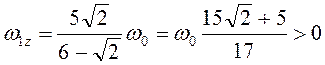 (
(![]() сонаправлена
с осью
сонаправлена
с осью ![]() ).
).
Для наиболее удаленного
от центра диска положения ![]()
![]() . (3.10)
. (3.10)
В момент времени ![]() , соответствующий положению
, соответствующий положению ![]() ,
,
![]() .
.
Так как 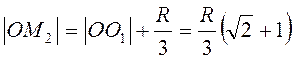 , то
, то 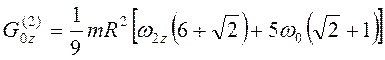 .
.
Далее из (3.10) следует 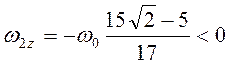 (
(![]() противонаправлена
оси
противонаправлена
оси ![]() ).
).
Ответ: 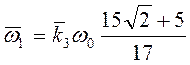 ,
, 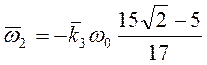 .
.
 9. 1-й способ.
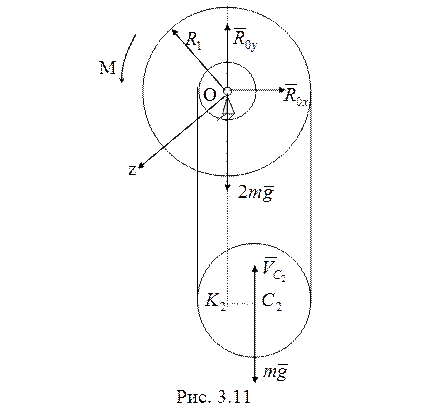
Внешние силы, действующие на систему, показаны на рис. 3.11. Составить
уравнение, описывающее движение системы и не содержащее неизвестных сил реакции
9. 1-й способ.
Внешние силы, действующие на систему, показаны на рис. 3.11. Составить
уравнение, описывающее движение системы и не содержащее неизвестных сил реакции
![]() позволяет теорема об изменении кинетического
момента относительно оси
позволяет теорема об изменении кинетического
момента относительно оси ![]() , так как моменты
, так как моменты ![]() .
.
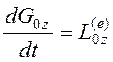 (3.11)
(3.11)
Кинетический момент системы
![]() .
.
Моменты инерции однородных дисков
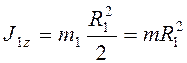 ,
, 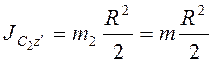 .
.
Мгновенный центр скоростей диска 2
расположен в точке ![]() , поэтому
, поэтому ![]() ,
а скорость точки
,
а скорость точки ![]() :
: ![]() .
.
Тогда ![]() .
.
Главный момент внешних
сил ![]() . Тогда из (3.11) следует
. Тогда из (3.11) следует
![]() .
.
Угловое ускорение 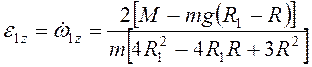 .
.
2-й способ. Теорема об изменении кинетической
энергии также позволяет составить дифференциальное уравнение движения системы,
не содержащее неизвестных реакций ![]() ,
, ![]() , так как они приложены в неподвижной точке
и не совершает работу.
, так как они приложены в неподвижной точке
и не совершает работу.
![]()
Кинетическая энергия ![]() . При вращательном движении
. При вращательном движении 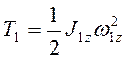 , при плоскопараллельном движении
, при плоскопараллельном движении 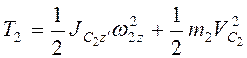 , т.е.
, т.е.
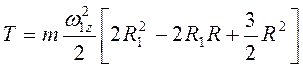 .
.
Элементарная работа сил ![]() . Поэтому
. Поэтому
![]() .
.
Так как ![]() , то
, то 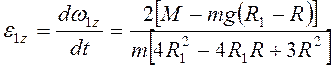 .
.
Ответ: 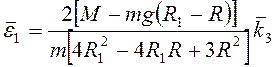 .
.
 10. Внешние силы, действующие на
систему, показаны на рис. 3.12. По теореме об изменении кинетического момента
стержня АВ вместе с грузом и ползуном относительно оси
10. Внешние силы, действующие на
систему, показаны на рис. 3.12. По теореме об изменении кинетического момента
стержня АВ вместе с грузом и ползуном относительно оси ![]()
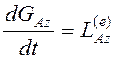 .
.
Так как ![]() ,
,
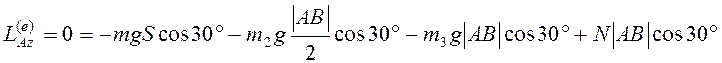 , и
реакция направляющих ползуна
, и
реакция направляющих ползуна 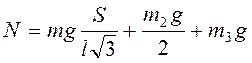 .
.
По теореме об изменении
кинетического момента всей системы относительно оси ![]()
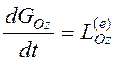 . (3.12)
. (3.12)
Так как ![]() ,
,
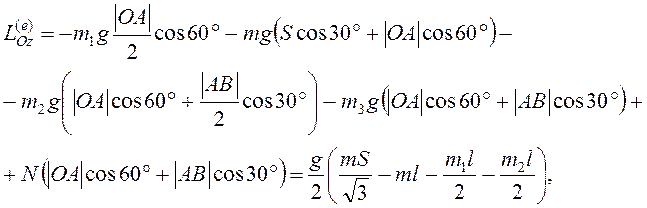
то из (3.12) следует
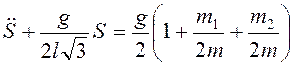 .
.
Начальные условия к полученному
уравнению ![]() . Решение для
. Решение для
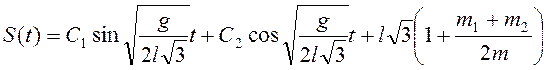 .
.
Из начальных условий следует 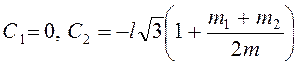 , т.е.
, т.е.
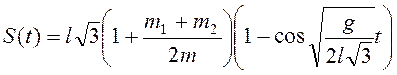 .
.
Ответ: 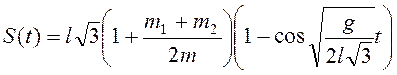 .
.
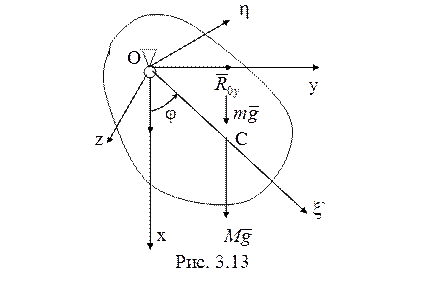 11. Рассмотрим
произвольный плоский физический маятник (рис. 3.13). Внешние силы показаны на рисунке.
Система координат
11. Рассмотрим
произвольный плоский физический маятник (рис. 3.13). Внешние силы показаны на рисунке.
Система координат ![]() жестко связана с маятником. По
теореме об изменении кинетического момента относительно оси
жестко связана с маятником. По
теореме об изменении кинетического момента относительно оси ![]()
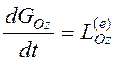 .
.
В отсутствие
присоединенной точечной массы ![]() , так как
, так как ![]() ,
, ![]() ,
следует уравнение
,
следует уравнение
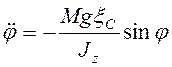 . (3.13)
. (3.13)
При наличии присоединенной массы в
точке с координатами (![]() )
)
![]() ,
, ![]() , и
, и
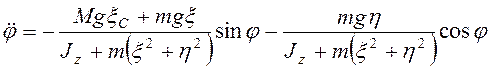 . (3.14)
. (3.14)
Движения маятника без
присоединенной точечной массы и с ней совпадают при совпадении уравнений (3.13)
и (3.14), то есть при совпадении коэффициентов при линейно независимых ![]() и
и ![]() в
правых частях этих уравнений. Поэтому
в
правых частях этих уравнений. Поэтому
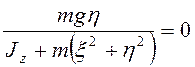 ,
,
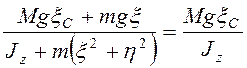 , т.е.
, т.е. ![]() или
или 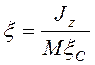 .
.
Случай помещения присоединенной массы
в точку подвеса ![]() тривиален и очевиден. Случай
тривиален и очевиден. Случай 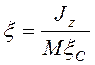 ,
, ![]() более
интересен.
более
интересен.
Замечание. Формула 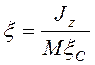 была
получена Х. Гюйгенсом. Точка с указанными координатами называется центром
качания.
была
получена Х. Гюйгенсом. Точка с указанными координатами называется центром
качания.
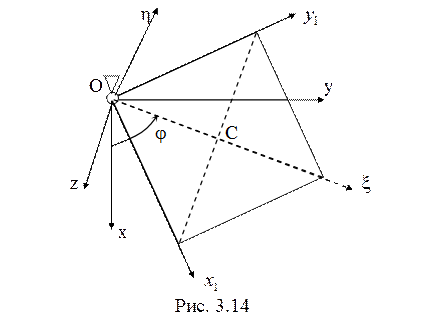 Для квадрата (рис.
3.14) стороны
Для квадрата (рис.
3.14) стороны ![]()
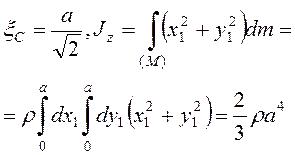
(![]() -
плотность). Если
-
плотность). Если ![]() - площадь квадрата, то
- площадь квадрата, то ![]() , и
, и 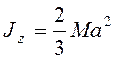 .
Отсюда
.
Отсюда 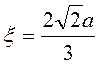 .
.
Ответ: на прямой ОС на
расстоянии ![]() от точки подвеса.
от точки подвеса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.