











23. По теореме об изменении кинетической энергии
![]() (3.30)
(3.30)
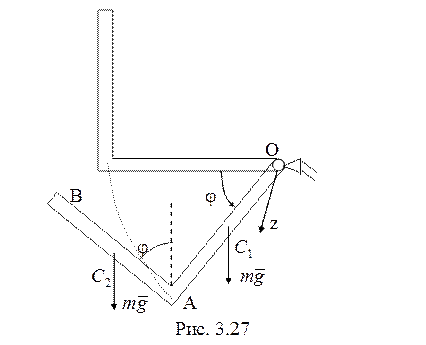 Кинетическая энергия вращающегося
уголка (рис. 3.27)
Кинетическая энергия вращающегося
уголка (рис. 3.27) ![]() . Момент инерции относительно оси
. Момент инерции относительно оси
![]()
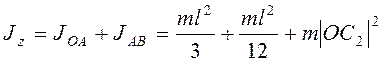 .
.
Так как 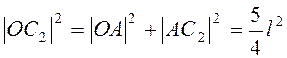 , то
, то 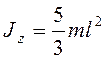 ,
, 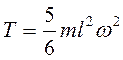 (
(![]() – масса стержня).
– масса стержня).
Работа сил тяжести стержней
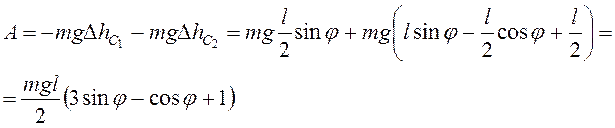 .
.
Тогда из (3.30) следует 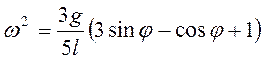 . Для функции
. Для функции
![]()
![]() ,
,
![]() при
при
![]() .
.
При ![]() , при
, при ![]() . Максимум угловой скорости достигается при
. Максимум угловой скорости достигается при
![]() .
.
При ![]()
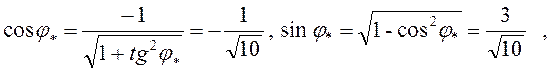
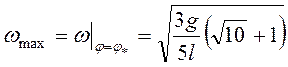 .
.
Ответ: 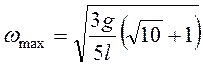 .
.
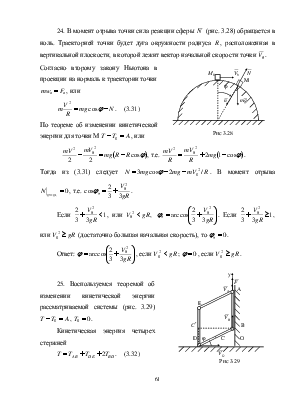
24. В момент отрыва точки
сила реакции сферы ![]() (рис. 3.28) обращается в ноль.
Траекторией точки будет дуга окружности радиуса
(рис. 3.28) обращается в ноль.
Траекторией точки будет дуга окружности радиуса ![]() , расположенная
в вертикальной плоскости, в которой лежит вектор начальной скорости точки
, расположенная
в вертикальной плоскости, в которой лежит вектор начальной скорости точки ![]() .
.
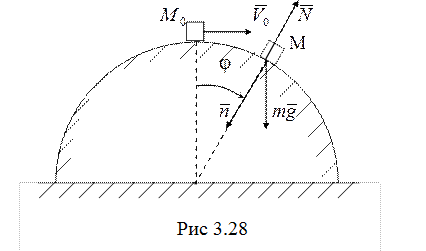 Согласно второму закону Ньютона в
проекции на нормаль к траектории точки
Согласно второму закону Ньютона в
проекции на нормаль к траектории точки
![]() , или
, или
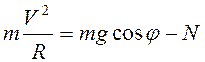 . (3.31)
. (3.31)
По теореме об изменении кинетической
энергии для точки М ![]() , или
, или
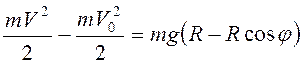 , т.е.
, т.е.
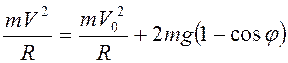 .
.
Тогда из (3.31) следует ![]() . В момент отрыва
. В момент отрыва ![]() ,
т.е.
,
т.е. 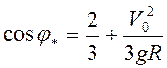 .
.
Если 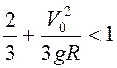 , или
, или 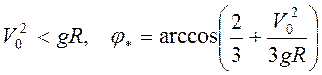 . Если
. Если
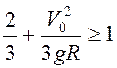 , или
, или ![]() (достаточно
большая начальная скорость), то
(достаточно
большая начальная скорость), то ![]() .
.
Ответ: 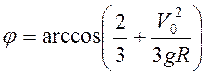 , если
, если ![]() ;
; ![]() , если
, если ![]() .
.
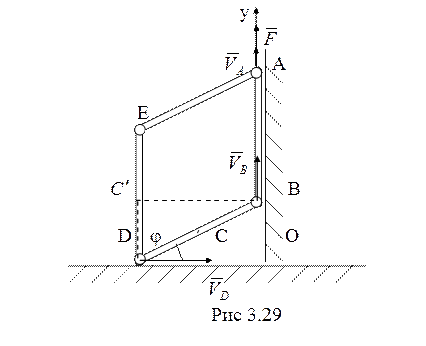
25. Воспользуемся
теоремой об изменении кинетической энергии рассматриваемой системы (рис. 3.29) ![]() ,
, ![]() .
.
Кинетическая энергия четырех стержней
![]() . (3.32)
. (3.32)
При поступательном движении ![]() . Из условия недеформируемости стержня BD проекции скоростей
. Из условия недеформируемости стержня BD проекции скоростей ![]() , т.е.
, т.е. ![]() . Так
как
. Так
как ![]() , то
, то ![]() , и
, и
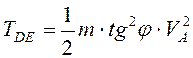 .
.
Кинетические энергии
стержней АЕ и BD равны. При плоскопараллельном
движении в текущем положении точка ![]() является мгновенным
центром скоростей стержня BD, и
является мгновенным
центром скоростей стержня BD, и ![]() . Момент инерции
. Момент инерции
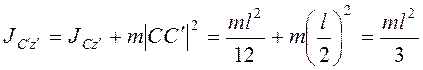 ,
угловая скорость
,
угловая скорость
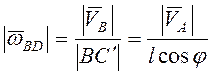 ,
и
,
и 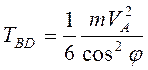 .
.
Тогда кинетическая энергия всей системы из (3.32)
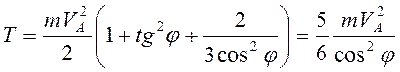 .
.
Работа сил тяжести
стержней АВ, BD и АЕ и силы ![]()
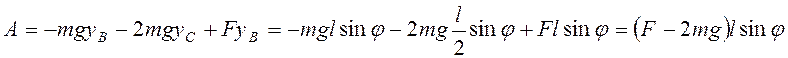 .
.
При ![]() силы
силы ![]() недостаточно, чтобы начать подъем
рассматриваемой системы.
недостаточно, чтобы начать подъем
рассматриваемой системы.
Из теоремы об изменении кинетической энергии системы следует, что
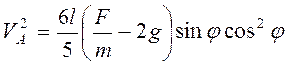 . (3.33)
. (3.33)
Рассмотрим функцию ![]() . Ее производная
. Ее производная
![]() .
.
На интервале ![]() ,
когда возможно показанное на рис. 3.29 текущее положение системы,
,
когда возможно показанное на рис. 3.29 текущее положение системы, ![]() при
при 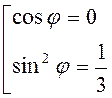 , или
, или 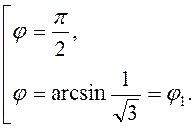
При ![]()
![]() (
(![]() возрастает),
при
возрастает),
при ![]()
![]()
(![]() убывает).
Скорость точки А максимальна при
убывает).
Скорость точки А максимальна при ![]() и, как следует из
(3.33),
и, как следует из
(3.33), 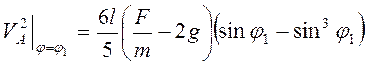 , т.е.
, т.е. 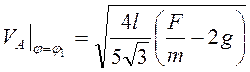 .
.
Ответ: 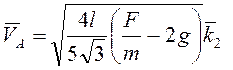 .
.
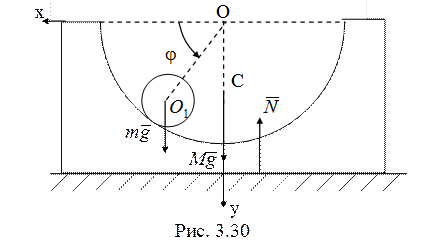 26. Рассматриваемая
система (рис. 3.30) имеет две степени свободы. Ее положение будем задавать
смещением тела
26. Рассматриваемая
система (рис. 3.30) имеет две степени свободы. Ее положение будем задавать
смещением тела ![]() вдоль горизонтальной плоскости и
углом
вдоль горизонтальной плоскости и
углом ![]() , который прямая
, который прямая ![]() образует
с горизонталью. Внешние силы, действующие на систему, показаны на рис. 3.30. Горизонтальная составляющая их
главного вектора
образует
с горизонталью. Внешние силы, действующие на систему, показаны на рис. 3.30. Горизонтальная составляющая их
главного вектора ![]() , в начальный момент времени система
покоилась, поэтому составляющая импульса системы
, в начальный момент времени система
покоилась, поэтому составляющая импульса системы ![]() . Но
. Но ![]() . Так как
. Так как ![]()
![]() , то
, то ![]() , и
, и ![]() , т.е.
, т.е. ![]() (3.34)
(3.34)
Работу в рассматриваемой
системе совершает только консервативная стационарная сила тяжести цилиндра, и
выполнен закон сохранения механической энергии ![]() . Кинетическая
энергия системы
. Кинетическая
энергия системы
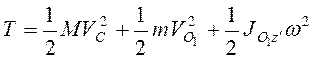 . (3.35)
. (3.35)
Скорости точек ![]() . Воспользовавшись теоремой косинусов, имеем
. Воспользовавшись теоремой косинусов, имеем
![]() .
.
Так как тело с выемкой движется
поступательно, то угловая скорость цилиндра равна его угловой скорости
относительно тела. В этом относительном движении точка касания цилиндра и тела
является мгновенным центром скоростей, и 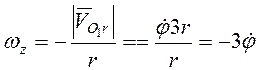 . Момент
инерции цилиндра
. Момент
инерции цилиндра 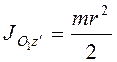 . Подставив последние формулы в
(3.35), получим для кинетической энергии системы
. Подставив последние формулы в
(3.35), получим для кинетической энергии системы
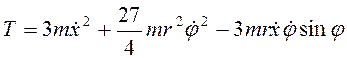 .
.
Потенциальная энергия системы
![]() .
.
В начальный момент времени ![]() ,
, 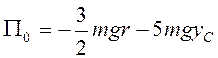 , и из
закона сохранения механической энергии системы получим
, и из
закона сохранения механической энергии системы получим
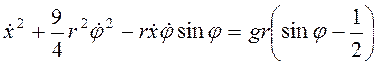 . (3.36)
. (3.36)
Совместным решением (3.34) и (3.36)
при ![]() , соответствующем нижнему положению оси цилиндра,
найдем
, соответствующем нижнему положению оси цилиндра,
найдем 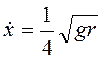 (в момент первого прохождения крайнего
нижнего положения).
(в момент первого прохождения крайнего
нижнего положения).
Ответ: 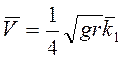 .
.
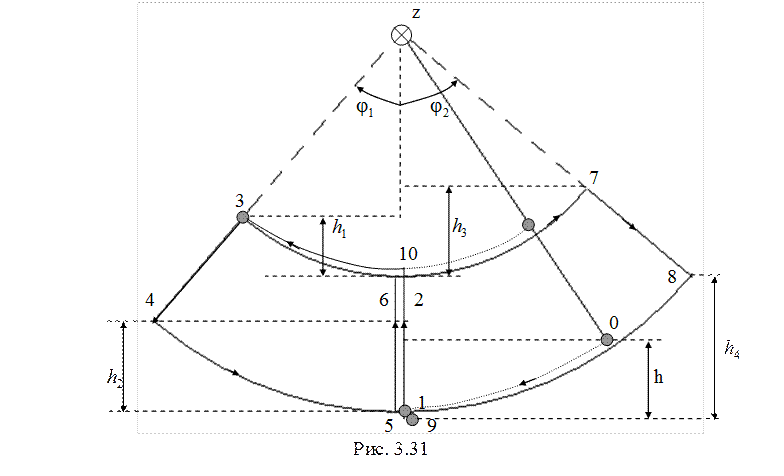
27. Рассмотрим движение модели качелей в виде описанного в условии задачи математического маятника (рис. 3.31) за один цикл.
На участке 0-1 по теореме
об изменении кинетической энергии ![]() , или
, или ![]() , т.е.
, т.е. ![]() . При
сокращении длины стержня на участке 1-2 в соответствии с теоремой об изменении
кинетического момента относительно оси, проходящей через точку подвеса
перпендикулярно плоскости
. При
сокращении длины стержня на участке 1-2 в соответствии с теоремой об изменении
кинетического момента относительно оси, проходящей через точку подвеса
перпендикулярно плоскости
 |
На участке подъема 2-3 ![]() , или
, или ![]() , т.е.
, т.е. 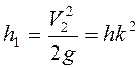 . Далее происходит мгновенное
восстановление длины стержня. При опускании (участок 4-5)
. Далее происходит мгновенное
восстановление длины стержня. При опускании (участок 4-5) ![]() , или
, или ![]() .
Изменение высоты
.
Изменение высоты ![]() . Так как
. Так как 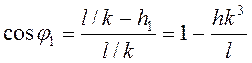 ,
то
,
то ![]() ,
, 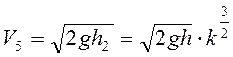 . При
сокращении длины стержня
. При
сокращении длины стержня 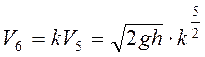 .
.
При подъеме (участок 6-7)
![]() , или
, или ![]() , т.е.
, т.е. ![]() . После восстановления длины стержня (7-8)
идет опускание (участок
. После восстановления длины стержня (7-8)
идет опускание (участок
8-9), и ![]() , или
, или ![]() . Так как
. Так как ![]() ,
, 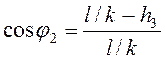 , то
, то ![]() ,
, ![]() . После мгновенного сокращения длины
стержня
. После мгновенного сокращения длины
стержня ![]() .
.
Если ![]() – скорости попадания точки в положение 2,
10, 18…, то
– скорости попадания точки в положение 2,
10, 18…, то ![]() . Соответственно
. Соответственно ![]() ,…,
,…,
![]() . При совершении полного оборота после N-попадания в крайнее нижнее положение
по теореме об изменении кинетической энергии должно быть выполнено условие
. При совершении полного оборота после N-попадания в крайнее нижнее положение
по теореме об изменении кинетической энергии должно быть выполнено условие 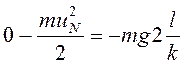 , т.е.
, т.е. 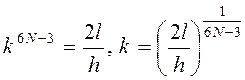 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.