Ответ: 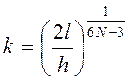 .
.
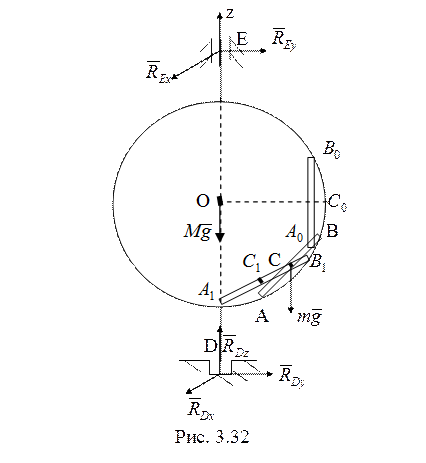 28. Рассматриваемая система (рис. 3.32)
имеет две степени свободы: поворот окружности и движение стержня относительно
окружности. Главный момент внешних сил тяжести и реакции подшипников D и Е относительно оси
28. Рассматриваемая система (рис. 3.32)
имеет две степени свободы: поворот окружности и движение стержня относительно
окружности. Главный момент внешних сил тяжести и реакции подшипников D и Е относительно оси ![]()
![]() , поэтому кинетический момент
системы
, поэтому кинетический момент
системы
![]() .
(3.37)
.
(3.37)
В начальный момент
времени ![]() . Момент инерции окружности относительно
оси вращения
. Момент инерции окружности относительно
оси вращения ![]() , момент инерции относительно
этой же оси параллельно расположенного стержня
, момент инерции относительно
этой же оси параллельно расположенного стержня
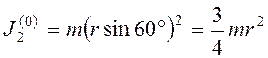 ,
и
,
и 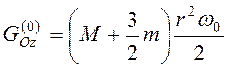 .
.
В момент остановки
стержня относительно окружности, соответствующий положению ![]() ,
, ![]() ,
, 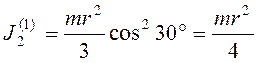 , и
, и
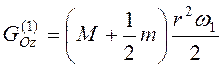 . Тогда
из (3.37) следует, что
. Тогда
из (3.37) следует, что 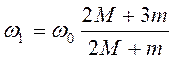 .
.
Работу на рассматриваемом интервале времени совершает только консервативная стационарная сила тяжести стержня, поэтому выполняется закон сохранения механической энергии
![]() . (3.38)
. (3.38)
Так как 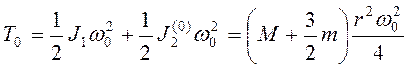 ,
, ![]() ,
,
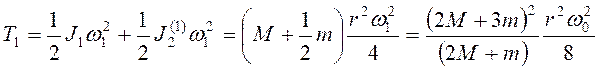 ,
,
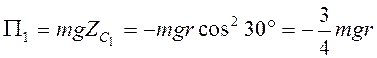 , то из (3.38) следует, что искомая
, то из (3.38) следует, что искомая
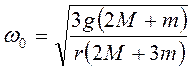 .
.
Ответ: 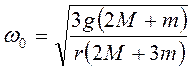 .
.
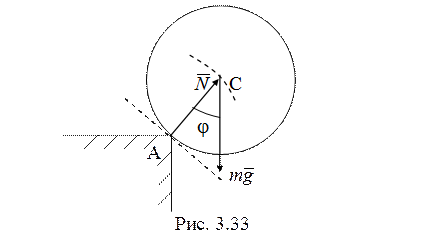 29. Внешние силы,
действующие на цилиндр после удаления опоры В, показаны на рис. 3.33. По
теореме об изменении кинетического момента относительно центра масс С в
проекции на ось, перпендикулярно плоскости движения цилиндра
29. Внешние силы,
действующие на цилиндр после удаления опоры В, показаны на рис. 3.33. По
теореме об изменении кинетического момента относительно центра масс С в
проекции на ось, перпендикулярно плоскости движения цилиндра 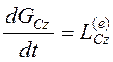 . Главный момент внешних сил
. Главный момент внешних сил ![]() , и
, и ![]() . Поэтому
угловая скорость
. Поэтому
угловая скорость ![]() , и после удаления опоры В
цилиндр движется поступательно. Так как до отрыва от опоры А
, и после удаления опоры В
цилиндр движется поступательно. Так как до отрыва от опоры А ![]() , то центр масс С движется по окружности радиуса
, то центр масс С движется по окружности радиуса
![]() с центром в точке А. По теореме о движении
центра масс в проекции на нормаль к его траектории
с центром в точке А. По теореме о движении
центра масс в проекции на нормаль к его траектории
![]() . (3.38)
. (3.38)
В начальный момент времени 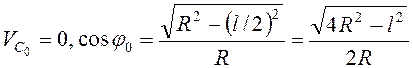 , и
, и
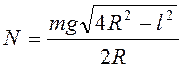 .
.
Так как изменение кинетической энергии равно работе силы тяжести цилиндра, то
![]() . (3.39)
. (3.39)
В момент отрыва при ![]() реакция опоры А
реакция опоры А ![]() ,
и совместное решение (3.38) и (3.39) дает
,
и совместное решение (3.38) и (3.39) дает 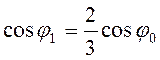 .
Вертикальное перемещение центра масс к этому моменту времени равно изменению
его высоты
.
Вертикальное перемещение центра масс к этому моменту времени равно изменению
его высоты
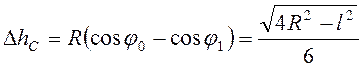 .
.
Ответ: 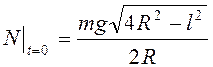 ,
, 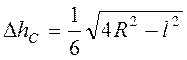 .
.
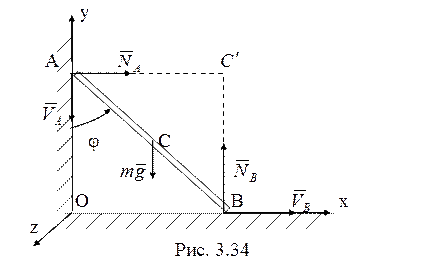 30. Рассмотрим
движение стержня до отрыва от вертикальной стенки (рис. 3.34). Работу при этом
падении совершает только консервативная стационарная сила тяжести, и
30. Рассмотрим
движение стержня до отрыва от вертикальной стенки (рис. 3.34). Работу при этом
падении совершает только консервативная стационарная сила тяжести, и
![]() . (3.40)
. (3.40)
Кинетическая энергия стержня
![]() (точка
(точка
![]() - мгновенный центр скоростей стержня). Момент
инерции
- мгновенный центр скоростей стержня). Момент
инерции 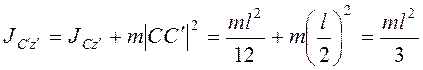 , составляющая угловой скорости
, составляющая угловой скорости ![]() , и
, и ![]() .
.
Потенциальная энергия 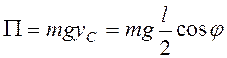 . Тогда из (3.40) следует
. Тогда из (3.40) следует
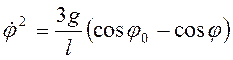 . (3.41)
. (3.41)
Отрыв от вертикальной
стенки наступает, когда ее реакция ![]() . По теореме о движении
центра масс
. По теореме о движении
центра масс
![]() . (3.42)
. (3.42)
Так как 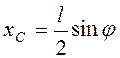 , то
, то 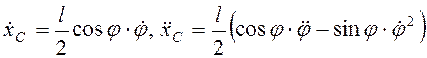 . Дифференцируя (3.41) по времени получим
. Дифференцируя (3.41) по времени получим 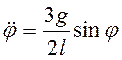 . Подставив полученные выражения в (3.42)
найдем
. Подставив полученные выражения в (3.42)
найдем 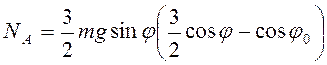 .
.
В момент отрыва ![]() . Так как
. Так как ![]() , и
, и ![]() , то
, то 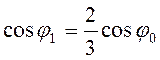 .
Угловая скорость в этот момент времени, согласно (3.41),
.
Угловая скорость в этот момент времени, согласно (3.41), 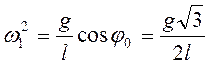 , т.е.
, т.е. 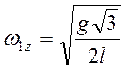 .
.
После отрыва от стенки
(рис. 3.35) ![]() , т.е.
, т.е.
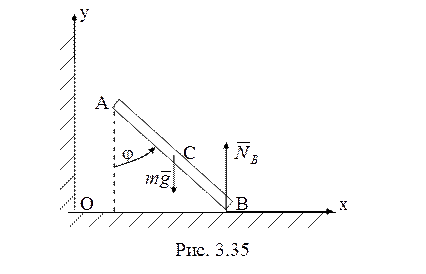
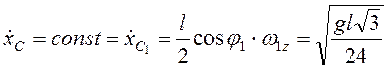 .
.
Кинетическая энергия при плоскопараллельном движении стержня
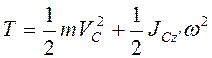 .
.
Для скорости центра масс 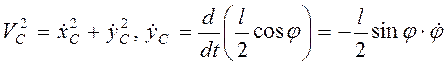 ,
,
момент инерции 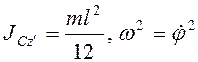 , и
, и 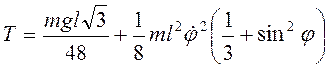 .
.
В момент падения при ![]() на основании (3.40) получим
на основании (3.40) получим 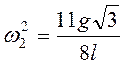 , т.е.
, т.е. 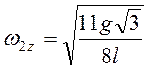 .
.
Ответ: 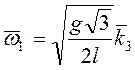 ,
, 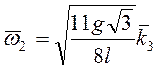 .
.
31. Рассматриваемая система (рис. 3.36) имеет две степени свободы. Для составления двух уравнений, описывающих ее закон движения, используем две теоремы динамики.
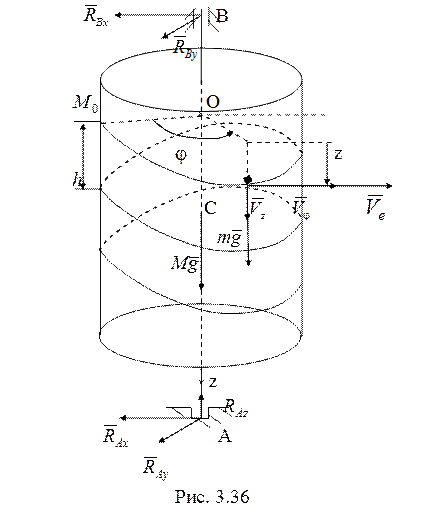 Внешние силы,
действующие на систему, показаны на рис. 3.36. Сумма моментов параллельных сил
тяжести и пересекающих ось
Внешние силы,
действующие на систему, показаны на рис. 3.36. Сумма моментов параллельных сил
тяжести и пересекающих ось ![]() сил реакции опоры
относительно указанной оси
сил реакции опоры
относительно указанной оси ![]() . Тогда кинетический
момент системы, учитывая начальные условия,
. Тогда кинетический
момент системы, учитывая начальные условия, ![]() . Но
. Но ![]() . Для цилиндра
. Для цилиндра 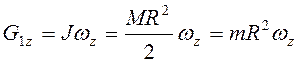 .
.
Для шарика
![]() . (3.43)
. (3.43)
Скорость шарика по теореме сложения
скоростей ![]() . Переносная скорость поворота шарика
вместе с цилиндром
. Переносная скорость поворота шарика
вместе с цилиндром ![]() . Для вычисления скорости шарика
относительно цилиндра используем связанную с цилиндром цилиндрическую систему
координат. Тогда
. Для вычисления скорости шарика
относительно цилиндра используем связанную с цилиндром цилиндрическую систему
координат. Тогда ![]() . Поэтому, согласно (3.43),
. Поэтому, согласно (3.43), ![]() . Спираль желоба описывается уравнением
. Спираль желоба описывается уравнением 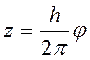 , то есть
, то есть ![]() , и
, и ![]() . Для всей системы
. Для всей системы ![]() ,
и
,
и ![]() .
.
По теореме об изменении
кинетической энергии системы ![]() ,
, ![]() ,
, ![]() .
Кинетическая энергия цилиндра
.
Кинетическая энергия цилиндра ![]() .
.
Кинетическая энергия шарика
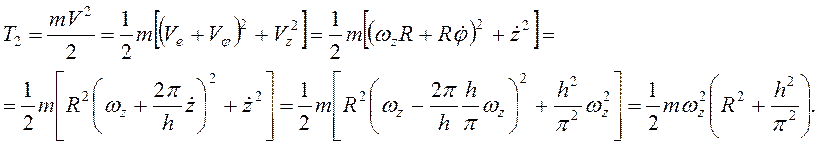
Работа силы тяжести шарика ![]() , поэтому
, поэтому 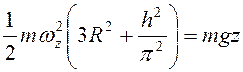 , и
, и
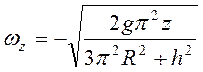 .
.
Ответ: 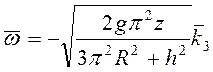 .
.
 |
Внешние силы, действующие
на систему, вертикальны. Их 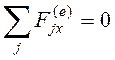 , следовательно,
горизонтальная составляющая импульса системы
, следовательно,
горизонтальная составляющая импульса системы ![]() .
.
В начальный момент времени
![]() .
.
В момент падения ![]() , т.е.
, т.е.
![]() . (3.44)
. (3.44)
Работу совершает только консервативная стационарная сила тяжести стержня, поэтому выполнен закон сохранения механической энергии
![]() . (3.45)
. (3.45)
В начальный момент времени кинетическая энергия системы
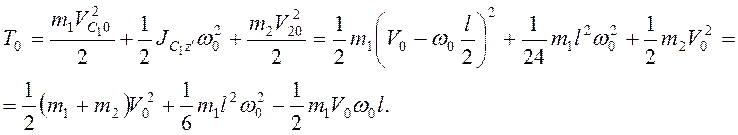
Потенциальная энергия системы ![]() .
.
В момент падения
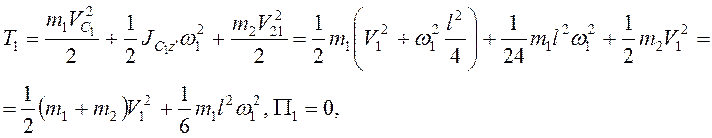
и согласно (3.45) ![]() .
.
Из (3.44) 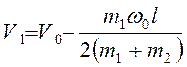 .
Подставляя это выражение в (3.46) после некоторых преобразований получим
.
Подставляя это выражение в (3.46) после некоторых преобразований получим 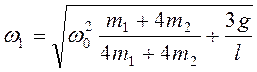 .
.
Ответ: 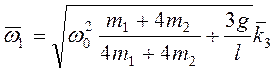 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.