Лабораторная работа №4
Тема: Исследование стойкости нелинейных систем по логарифмичным частотным характеристикам
Цель работы: научиться строить ЛАЧХ и ЛФЧХ линейной части, а также запретную зону; исследовать на устойчивость.
Ход работы
С помощью логарифмичных частотных характеристик можно исследовать абсолютную стойкость положения равновесия нелинейной системы.
Для определения стойкости системы необходимо построить ЛАЧХ и ЛФЧХ линейной части системы, а также запретную зону на площади логарифмических частотных характеристик.
Согласно варианту дана передаточная функция:
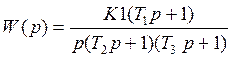
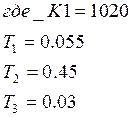
Подставив значения, получим
выражение: 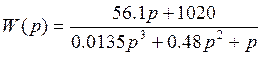
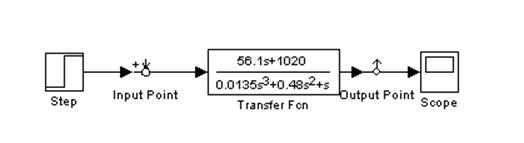
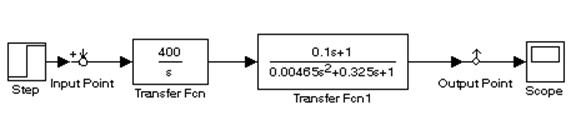
Построим ЛАЧХ и ЛФЧХ 2 способами
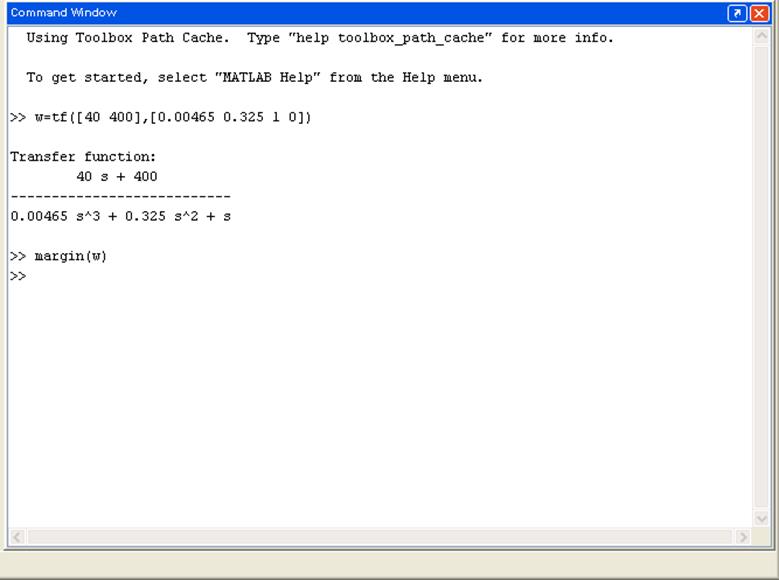
1.С помощью командного окна
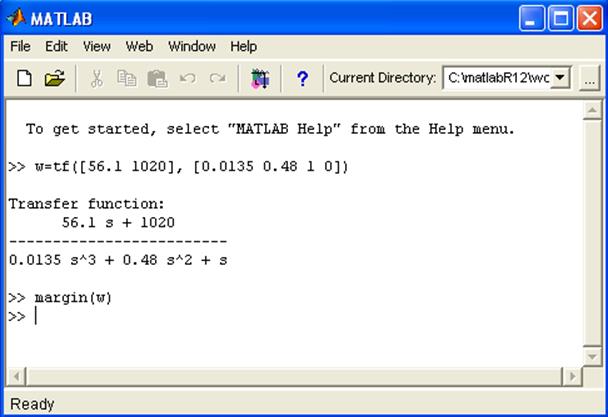
2.построим ЛАЧХ и ЛФЧХ с помощью TOOLS
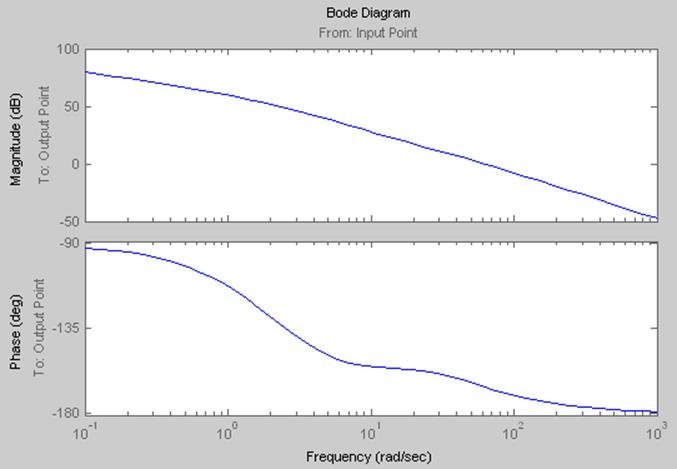
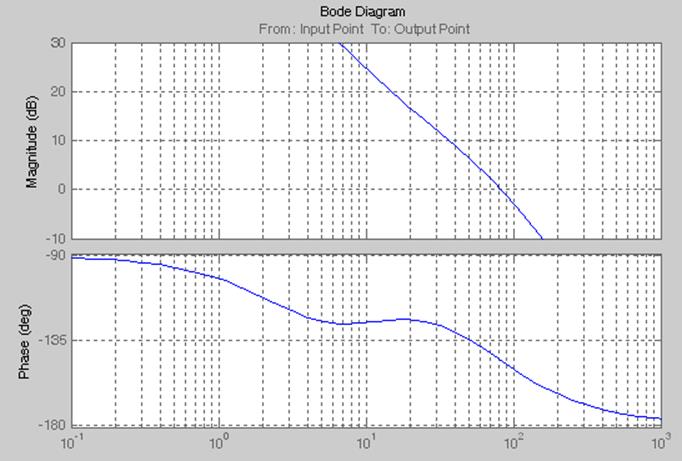
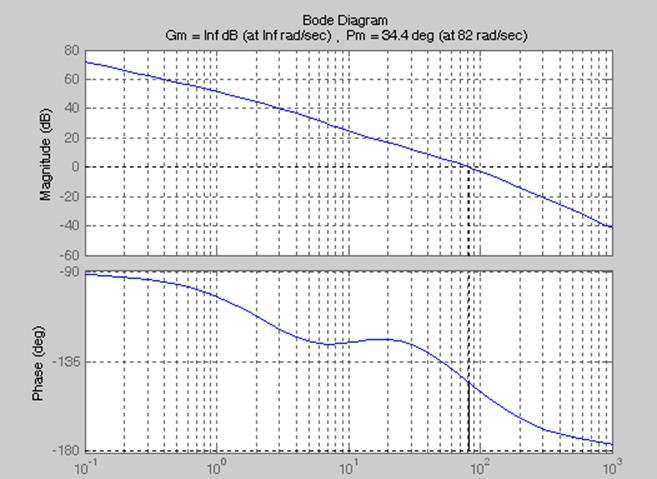
С помощью графика, представленного на рисунке 2, построим запретную зону
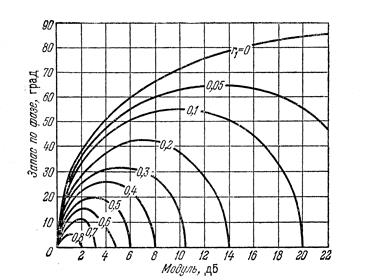
Необходимо определить значение r1-значение относительного наклона нижней границы сектора, в котором находится нелинейная характеристика при относительном наклоне верхней границы сектора, который равняется единице. Для нахождения значения r1 сектора [k1,k2], в котором характеристика нелинейного звена, нормируют таким образом, чтобы характеристика этого нелинейного звена принадлежало сектору [r1,1].
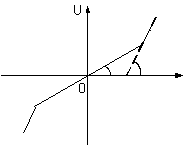
, значение относительного наклона
будет равно: 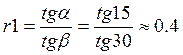
Выводы: В ходе данной лабораторной работы научились строить ЛАЧХ и
ЛФЧХ линейной части, запретную зону, а также изучили способ исследования
абсолютной устойчивости с помощью логарифмических частотных характеристик. В
результате расчетов и построения определили, что ЛФЧХ передаточной функции 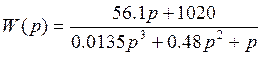 заходит в запретную
зону. А это значит, что система неустойчива.
заходит в запретную
зону. А это значит, что система неустойчива.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.