Визначення стійкості нелінійних систем за критерієм Попова

МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ

Кафедра КСУ

Звіт

по лабораторній роботі № 3

«Визначення стійкості нелінійних систем за критерієм Попова»

Виконав                                                                                     Студент групи СУ-42

Глушан В.О.    

Перевірив                                                                                                      Журба В.О

Суми 2008

Тема: Визначення стійкості нелінійних систем за критерієм Попова

Мета роботи – навчитися будувати модифіковану АФЧХ (криву Попова) лінійної частини системи в Matlab, визначити стійкість системи за критерієм Попова

Теоретичні відомості

Критерій Попова встановлює умови абсолютної стійкості. Абсолютна стійкість означає асимптотичну стійкість нелінійної системи у цілому (тобто відносно всього простору станів системи) за умови, що задано не конкретну не лінійність, а деякий клас нелінійностей М. Критерій Попова можна застосувати до класу стаціонарних нелінійностей, яким є множина М[k₁, k₂] усіх кусково-безперервних функцій, графіки яких знаходяться в секторі S[k₁, k₂] між лініями u = k₁ε та u = k₂ε (рис. 11). Ці нелінійності повинні задовольняти такі умови:

φ(ε) – безперервна функція,  φ(0) = 0;

ε φ(ε) > 0 при ε = 0;

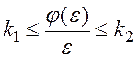    при ;

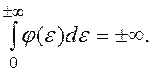
Абсолютна стійкість означає стійкість у цілому для всіх нелінійностей заданого класу.

Перед тим, як навести критерій Попова, введемо поняття прямої та кривої Попова. Прямою Попова називається пряма, що

проходить у комплексній площині через точку з координатами  (-1/k; 0j) і має кутовий коефіцієнт 1/q. Коефіцієнт k для однозначних нелінійностей (тобто для нелінійностей, характеристики яких містяться в секторі  S[0, k]) визначається з умови:

.

ε

u = k1ε

u = k2ε

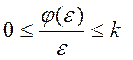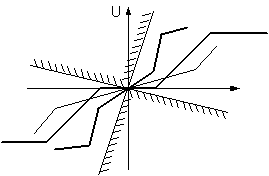
Рисунок 1 – Нелінійні характеристики, що належать сектору S[k₁, k₂]

Іншими словами, коефіцієнт k – верхня границя сектора, якому належить характеристика нелінійності.

Кутовий коефіцієнт 1/q визначається типом нелінійності, і для однозначних нелінійних характеристик параметр q вибирається з діапазону - ∞ < q < ∞, тобто пряму Попова можна проводити з будь-яким кутовим коефіцієнтом – як додатним, так і від’ємним.

Введемо тепер поняття видозміненої (модифікованої) частотної характеристики лінійної частини системи, або кривої Попова:

W_л^*(jω) = U_л (ω) + jωV_л(ω)

Вираз цієї характеристики: відрізняється від звичайної амплітудно-фазової характеристики W_л(jω) тільки тим, що уявна частина множиться на ω. Видозмінена характеристика W_л^*(jω) має такий самий вигляд, що й характеристика W_л(jω), тільки масштаб уявної частини змінюється у ω разів.

Сформулюємо тепер критерій Попова, або умови абсолютної стійкості: нелінійна система абсолютно стійка, якщо в площині W_л^*(jω) можна провести пряму Попова так, щоб крива Попова була праворуч від неї. Якщо таку пряму Попова провести неможливо, то абсолютна стійкість у досліджуваній системі неможлива.

Хід роботи

1. Зберемо схему для побудови кривої Попова.

Схема лінійної частини системи має вигляд:

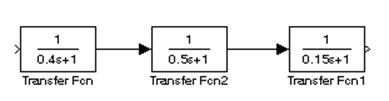
Характеристики нелінійної ланки та її параметри наведені нижче:

ε

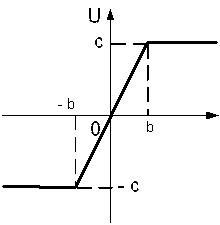
b = 1; c= 4

Для побудови кривої Попова необхідно виділити дійсну і уявну частину лінійної частини, після чого отримати модифіковану частотну характеристику лінійної частини системи.

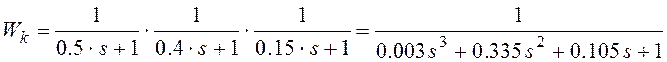
Зробимо заміну

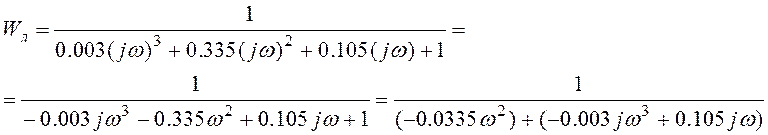
Помноживши чисельник та знаменник на вираз, комплексно зв'язаний зі знаменником, отримаємо вирази дійсної та уявної частин модифікованої амплітудно-фазової характеристики W_л(jω):

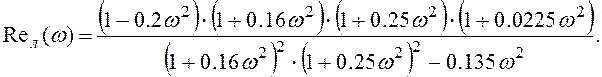
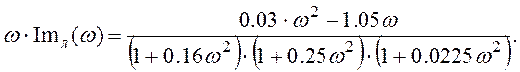
На основі отриманих результатів побудуємо криву Попова. Для цього зберемо в системі Matlab наступну схему:

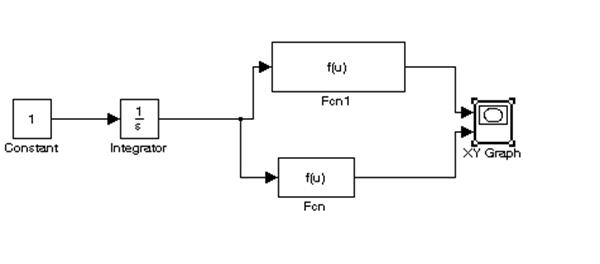
На цій схемі Fcn(u) - дійсна частин, Fcn1(u) – модифікована уявна частина модифікованої амплітудно-фазової характеристики W_л(jω). Провівши моделювання отримаємо криву Попова наступного вигляду:

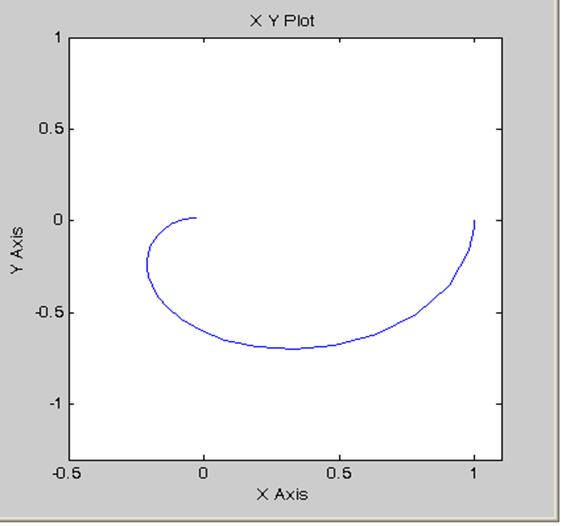
Рисунок 2 – крива Попова

Використавши задані параметри нелінійної ланки знайдемо координати точки, через яку проходить пряма Попова:

,

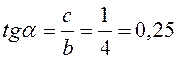Отже k=0,25. Тому точка, через яку проходитиме пряма Попова буде мати координати: ().

Проведемо в площині W^*_л(w)=X+jY пряму Попова. Нелінійна система буде абсолютно стійкою, якщо в площині W_л^*(jω) можна провести пряму Попова так, щоб крива Попова була праворуч від неї. Якщо таку пряму Попова провести неможливо, то абсолютна стійкість у досліджуваній системі неможлива. Як бачимо з рисунку для даної системи вищеназвана умова стійкості виконується. Отже задана система є абсолютно стійкою.

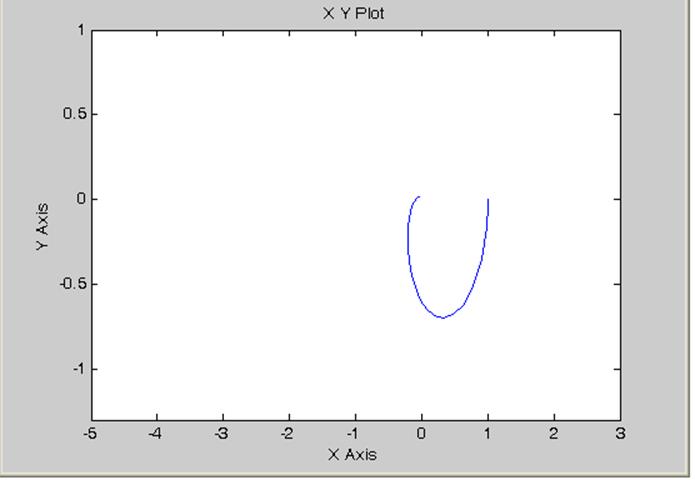
Рисунок 3 – Крива і пряма Попова

Висновок: виконавши лабораторну роботу, ми навчитися будувати модифіковану АФЧХ (криву Попова) лінійної частини системи в Matlab. Визначили за критерієм Попова, що задана система абсолютно стійка.