Дослідження стійкості нелінійних систем за логарифмічними частотними характеристиками

МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ

Кафедра КСУ

Звіт

по лабораторній роботі № 4

«Дослідження стійкості нелінійних систем за логарифмічними частотними характеристиками»

Виконав                                                                                     Студент групи СУ-42

Глушан В.О.

Перевірив                                                                                                      Журба В.О

Суми 2008Тема: Дослідження стійкості нелінійних систем за логарифмічними частотними характеристиками

Мета роботи – навчитися будувати ЛАЧХ та ЛФЧХ лінійної частини системи, а також заборонену зону; дослідити абсолютну стійкість положення рівноваги нелінійної системи

Теоретичні відомості

За допомогою логарифмічних частотних характеристик можна дослідити абсолютну стійкість положення рівноваги нелінійної системи.

Для визначення стійкості системи необхідно побудувати ЛАЧХ та ЛФЧХ лінійної частини системи, а також заборонену зону на площині логарифмічних частотних характеристик.

Побудова забороненої зони здійснюється за допомогою графіків, що наведені на рис. 1. Ці графіки пов’язують запас за фазою Δφ з модулем в децибелах для різних значень r₁.

r₁ – значення відносного нахилу нижньої границі сектора, в якому розташована нелінійна характеристика при відносному нахилі верхньої границі сектору, що дорівнює одиниці.

Для знаходження r₁ сектор [k₁, k₂],  в якому знаходиться характеристика нелінійної ланки, нормують так, щоб характеристика цієї нелінійної ланки належала сектору [r₁, 1]. Звідси видно, що r₁=k₁/k₂.

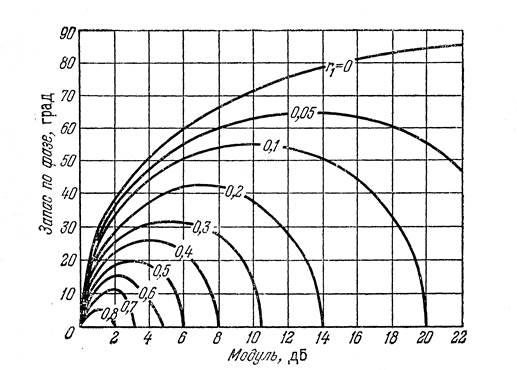
Рисунок 1 – Графіки, що пов’язують запас за фазою з модулем, в дБ, для різних r₁

Після побудови ЛЧХ та забороненої зони можна зробити висновок щодо стійкості нелінійної системи. Система стійка, якщо ЛФЧХ лінійної частини системи не заходить у заборонену зону, а якщо заходить – то система нестійка. Приклади логарифмічних частотних характеристик стійкої системи та забороненої зони наведені на рис. 14.

Хід роботи

1. Відповідно до варіанту передаточна функція лінійної ланки:

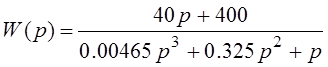
2. Побудуємо ЛАЧХ та ЛФЧХ лінійної частини системи двома способами (з командної строки Matlab та за допомогою меню Tools).

Введемо в командний рядок дані, необхідні для побудови  ЛАЧХ та ЛФЧХ:

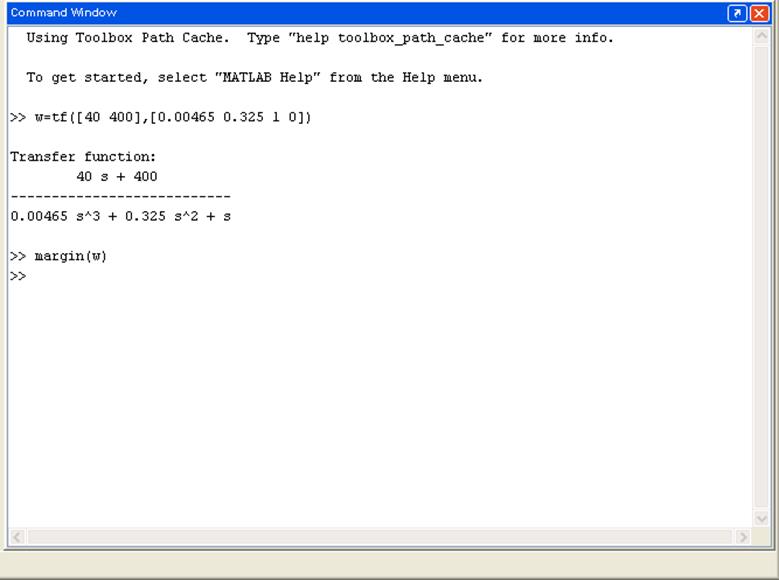
ЛАЧХ та ЛФЧХ лінійної частини системи зображено на рис.2:

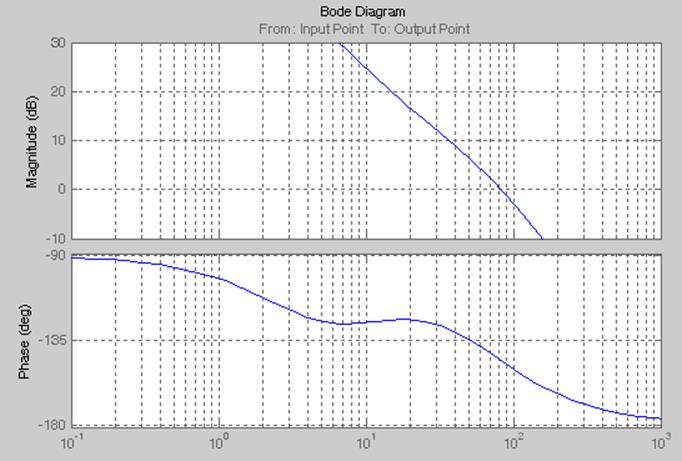
Рисунок 2 – Графіки ЛАЧХ та ЛФЧХ лінійної частини системи, побудовані з командного рядка Matlab

Для побудови ЛАЧХ та ЛФЧХ системи  за допомогою меню Tools зберемо в додатку simulink схему для моделювання поведінки системи:

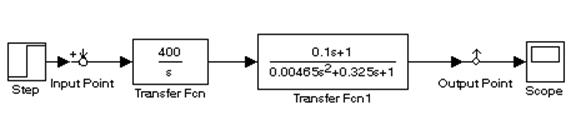
Отримали наступні графіки ЛАЧХ та ЛФЧХ, що зображені на рис.3:

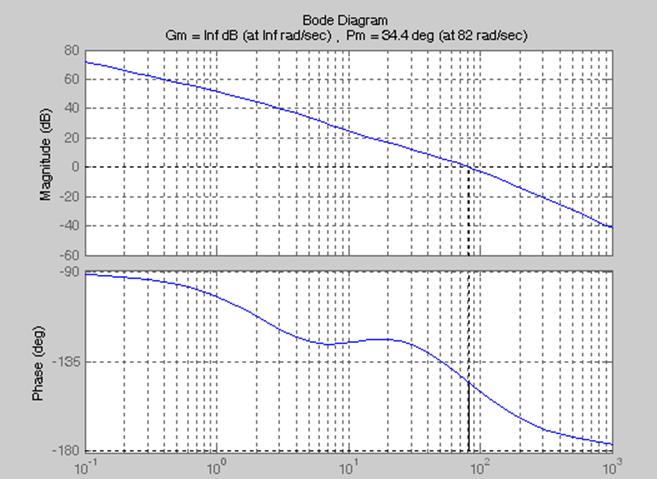
Рисунок 3 – Графіки ЛАЧХ та ЛФЧХ лінійної частини системи, побудовані а допомогою меню Tools

3. За допомогою графіків (рис. 1), що пов’язують запас за фазою з модулем в дБ для різних значень r₁, побудуємо заборонену зону для r₁ для заданої системи.

Необхідно визначити значення r₁- значення відносного нахилу нижньої границі сектора, в якому знаходиться нелінійна характеристика при відносному нахилі верхньої границі сектора, який дорівнює одиниці. Для знаходження r₁ сектор [k₁, k₂],  в якому знаходиться характеристика нелінійної ланки, нормують так, щоб характеристика цієї нелінійної ланки належала сектору [r₁, 1]. Звідси видно, що r₁=k₁/k₂, де , . Відповідно до варіанту α= 45˚, β= 59˚.

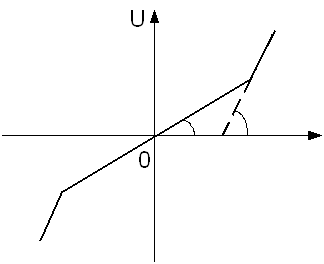
Тому значення відносного нахилу буде дорівнювати:

.

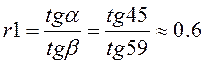Графік логарифмічних характеристик та забороненої зони приведено на рис. 4:

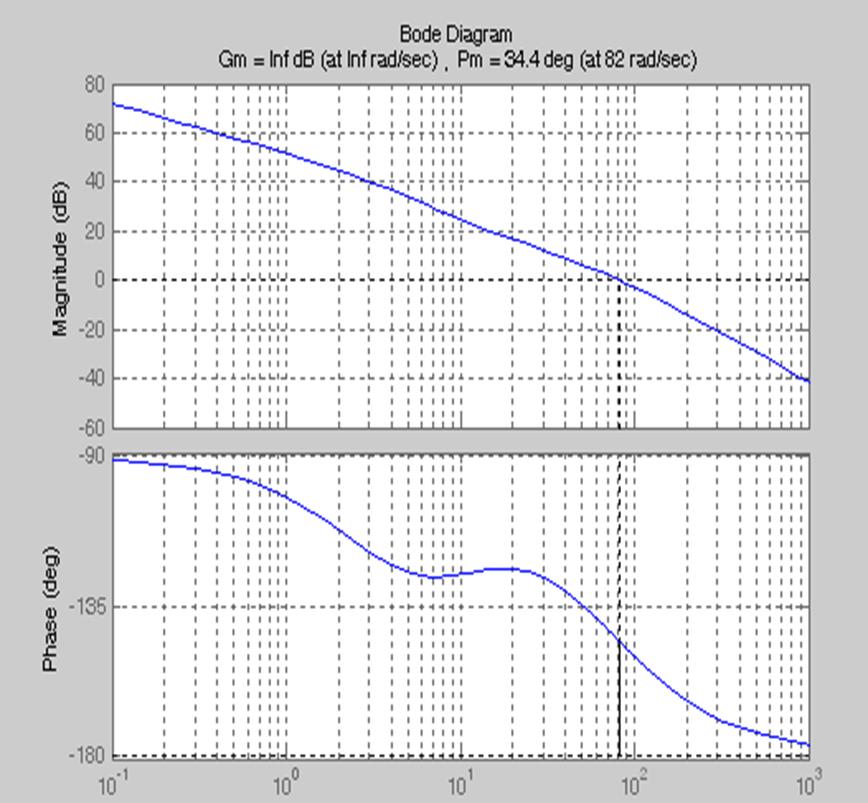
Рисунок 4 – Графік логарифмічних характеристик та забороненої зони

Висновок: виконавши лабораторну роботу, ми навчилися будувати ЛАЧХ та ЛФЧХ лінійної частини системи, а також заборонену зону; навчилися досліджувати стійкість положення рівноваги нелінійної системи за допомогою логарифмічних характеристик. В результаті моделювання та розрахунків визначили, що ЛФЧХ досліджуваної системи не заходить в заборонену зону. Отже система є стійкою.