Другие предметы \ Теория нелинейных и цифровых систем управления

Определение стойкости нелинейных систем по критерию Попова

Страницы работы

Уважаемые коллеги! Предлагаем вам разработку программного обеспечения под ключ.

Опытные программисты сделают для вас мобильное приложение, нейронную сеть, систему искусственного интеллекта, SaaS-сервис, производственную систему, внедрят или разработают ERP/CRM, запустят стартап.

Сферы - промышленность, ритейл, производственные компании, стартапы, финансы и другие направления.

Языки программирования: Java, PHP, Ruby, C++, .NET, Python, Go, Kotlin, Swift, React Native, Flutter и многие другие.

Всегда на связи. Соблюдаем сроки. Предложим адекватную конкурентную цену.

Заходите к нам на сайт и пишите, с удовольствием вам во всем поможем.

Содержание работы

Лабораторная работа №3

Определение стойкости нелинейных систем по критерию Попова

Цель работы: научиться строить модифицированную АФЧХ (кривую Попова) линейной части в MATLAB, определить стойкость по критерию Попова

Ход работы

Соберем схему для построения кривой Попова.

Т₁	0,2
Т₂	0,1
Т₃	0,5
Т₄	0,015

Линейная часть имеет вид:

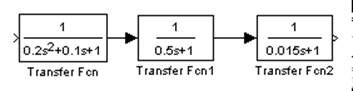
Характеристика нелинейного звена:

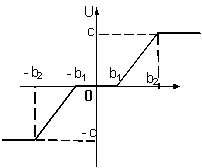
b₁= 0,5; b₂= 1; c = 6.

Для построения кривой Попова необходимо выделить действительную и мнимую часть линейной части, после чего получить модифицированную линейную часть.

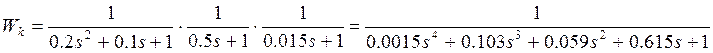
Делаем подстановку s=jw

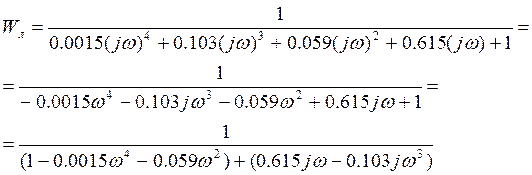
Действительная часть: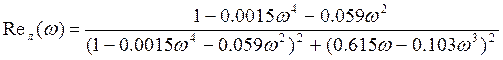

Мнимая часть: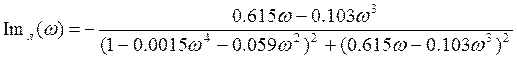

На основе полученных результатов построить кривую Попова

Соберем схему для построения кривой Попова.

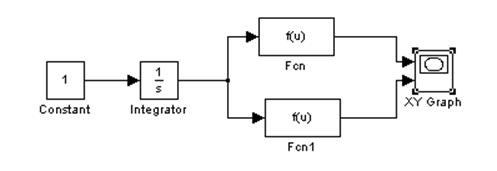
На данной схеме: является Fcn(u) - действительной частью

Fcn1(u) - модифицированной мнимой частью

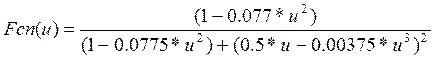
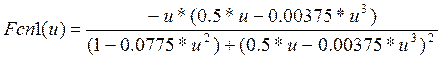
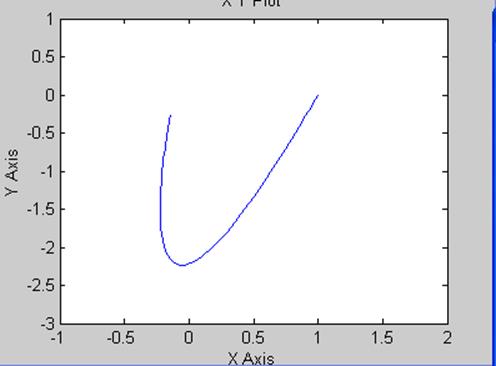
Рис.1 Кривая Попова

Из заданных параметров нелинейного звена находим координаты точки, через которую можно провести прямую Попова.

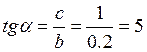
Координаты точки: ()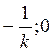

()

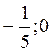Нелинейная система абсолютно устойчива если в плоскости W’л(w)=X+jY можно провести прямую Попова так, чтобы кривая Попова была справа от нее. Для данного случая это возможно, по этому система является абсолютно устойчивой.

Постоим прямую Попова

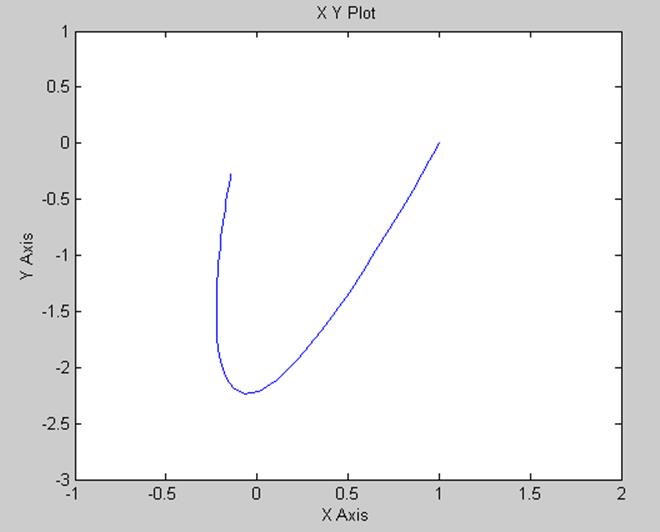
Рис.2 Кривая и прямая Попова

Выводы:

В ходе лабораторной работы научились строить модифицированную АФЧХ (кривую Попова) линейной части системы в MATLAB. Согласно критерию Попова определили, что данная система является абсолютно устойчивой.