Дослідження нелінійних систем методом фазової площини

МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ

Кафедра КСУ

Звіт

по лабораторній роботі № 2

«Дослідження нелінійних систем методом фазової площини»

Виконав                                                                                     Студент групи СУ-42

Глушан В.О.

Перевірив                                                                                                      Журба В.О

Суми 2008

Тема: Дослідження нелінійних систем методом фазової площини

Мета роботи – навчитися будувати фазові траєкторії нелінійних систем; знайти параметри автоколивань, що виникають у системі.

Теоретичні відомості

На відміну від лінійних систем стійкість нелінійних систем залежить не тільки від власних параметрів системи, але й від величини зовнішніх дій та місця їх прикладення. Тому не можна говорити про стійкість або нестійкість нелінійної системи взагалі, а можна розглядати стійкість або нестійкість різних режимів роботи системи при різних за величиною діях.

Специфічним динамічним режимом нелінійних систем, який не може бути в лінійних системах, є режим автоколивань. Автоколивання – це стійкі незгасаючі періодичні коливання, що виникають у нелінійних системах за умов відсутності зовнішніх періодичних дій. Амплітуда і частота автоколивань визначається тільки власними параметрами системи.

Багато особливостей динаміки нелінійних систем можна розглянути на прикладі систем другого порядку, використавши найпростіший варіант простору станів, а саме двовимірний простір або площину станів (фазову площину). За координати фазової площини беруть відхилення х вихідної величини від її значення, що відповідає усталеному режиму системи, і похідну у=dx/dt цього відхилення. Усталеному режиму системи другого порядку відповідає початок координат. Якщо будь-яка дія виводить систему з усталеного режиму, то зображуюча точка опиняється у довільному місці фазової площини. Під час перехідного процесу змінюється вихідна величина х та її похідна у, тому зображуюча точка рухається у фазовій площині по фазовій траєкторії. Початкове положення зображуючої точки відповідає початковим умовам вільного руху системи. Сукупність фазових траєкторій, що відповідають різним початковим станам системи, називається фазовим портретом. Фазовий портрет дає повне уявлення про динаміку нелінійної системи. Тому дослідження нелінійних систем методом фазової площини, по суті, зводиться до побудови фазового портрета і аналізу за його допомогою динамічних режимів системи.

Хід роботи

1. Зберемо схему нелінійної системи для побудови та дослідження фазових траєкторій

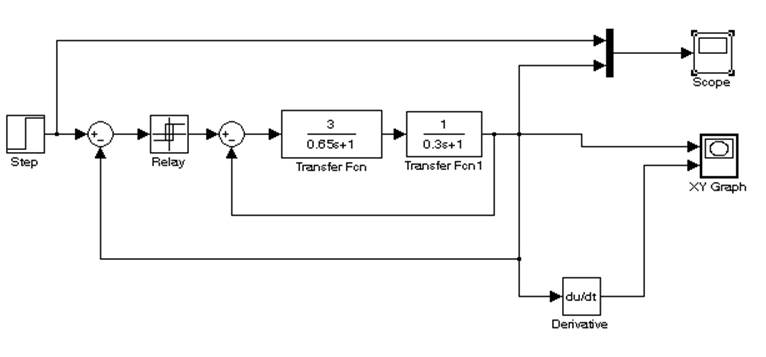
2. Змінюючи параметри системи, промоделюємо поведінку системи для отримання фазових траєкторій на фазовій площині, що відповідають різним початковим положенням системи. Отримані перехідні процеси та відповідні їм фазові траєкторії проілюстровано нижче(графіки а), б), в)).

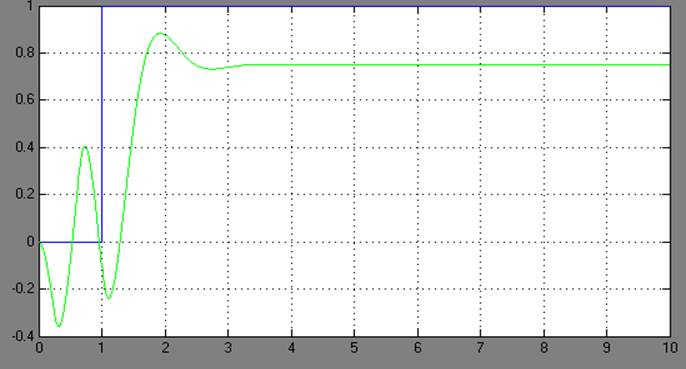
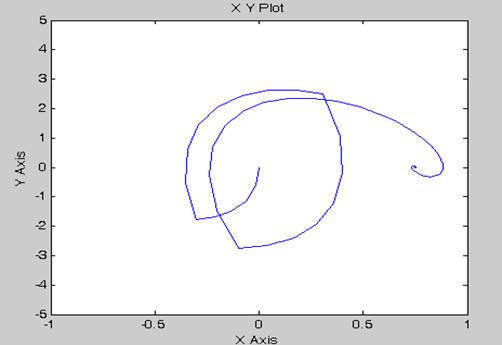
а)

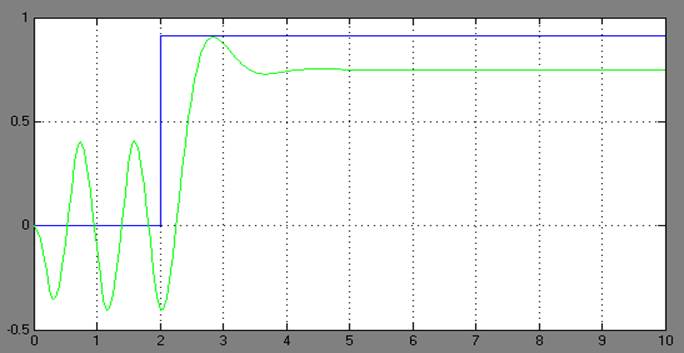
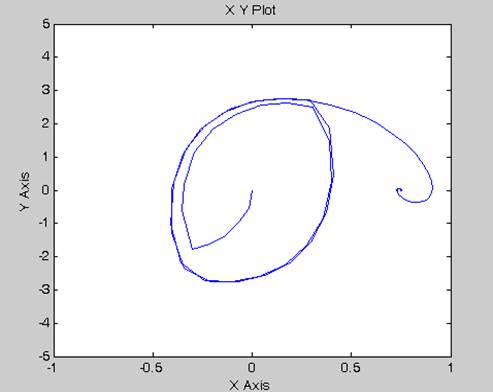
б)

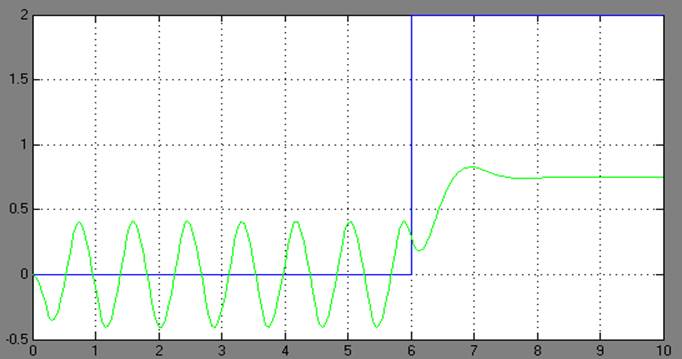
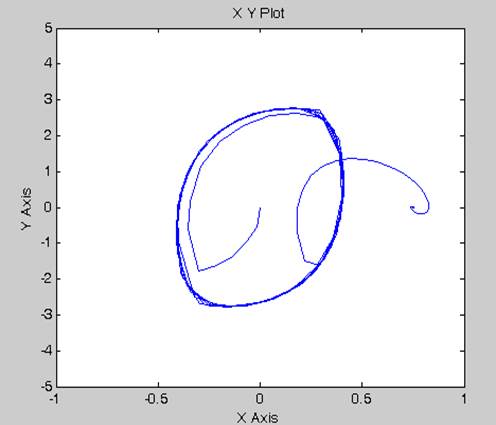
в)

3. Налаштуємо систему на режим автоколивань. Для отримання та дослідження режиму автоколивань необхідно виставити параметр Initial value, який не дорівнює нулю, параметр Final value блоку Step, який дорівнює нулю. Параметр Step time виставити таким, що не дорівнює нулю (наприклад, який дорівнює 2). Із цього моменту дана система переходить до режиму автоколивань. За початкове положення системи візьмемо значення вихідної координати х та її похідної у = dx/dt на момент часу Step time.

Для отримання різних початкових умов будемо змінювати параметри Step time та Initial value блоку Step. Проілюструємо поведінку системи графіками перехідних процесів та фазових траєкторій для різних значень параметрів блоку Step(графіки г), д), е)).

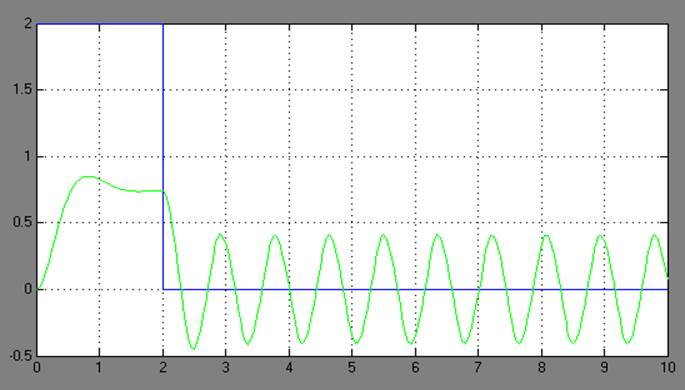
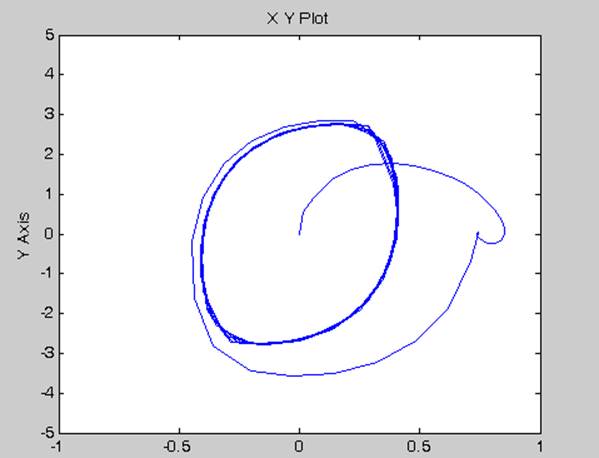
г)

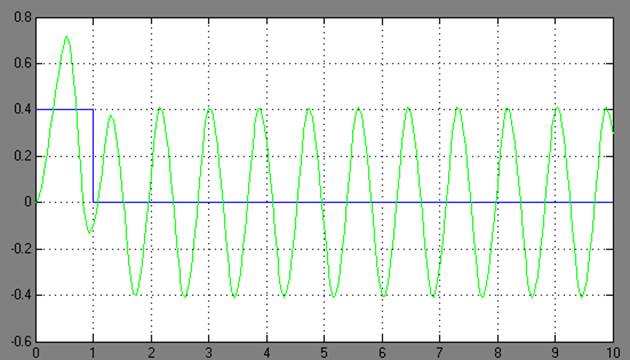
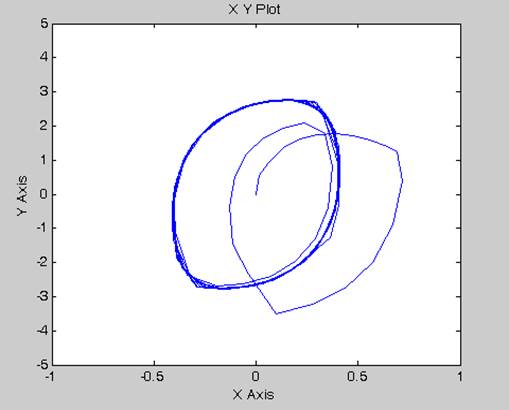
д)

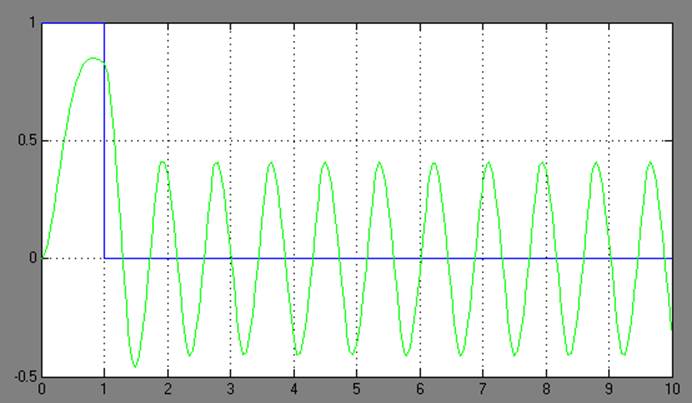
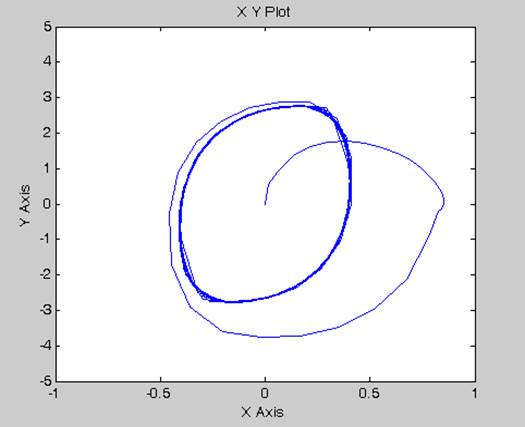
е)

4. За граничним циклом на фазовому портреті визначимо якісні та кількісні показники нелінійної системи в режимі автоколивань, а саме:

–  амплітуду автоколивань;

–  частоту автоколивань;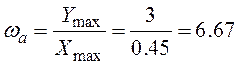

–  період автоколивань.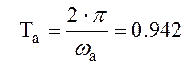

(х_max та у_max  – максимальні значення вихідної координати системи в режимі автоколивань та її похідної за часом відповідно).

Висновки: виконавши лабораторну роботу, ми навчитися будувати фазові траєкторії нелінійних систем; знайшли параметри автоколивань(амплітуду, частоту, період автоколивань), використавши для цього стійкий граничний цикл – замкнуту траєкторію на фазовій площині, що відповідає режиму автоколивань, що виникають у системі.