Дослідження нелінійної системи слідкуючого електропривода з редуктором

повороту виконуючої осі (ВВ) об’єкта регулювання;
ВС і ВЕ – пара сельсинів;
UВ – фазочутливий випрямляч;
А – підсилювач;
UМ – тиристорний перетворювач;
М – двигун з незалежним збудженням;
LМ – обмотка збудження двигуна;
q – редуктор;
ОУ – об’єкт управління.

Вимірюючий прилад –                                Θ_вх- Θ_вих=δ;                                                  (1)

Фазочутливий підсилювач UВ –                δ·к_фп=U_фп;                                          (2)

Підсилювач напруги А –                            U_фп·к_п= U_п;                                        (3)

Тиристорний перетворювач UМ –             U_п·к_мп= U_d,                                                 (4)

де к_фп, к_п, к_мп – коефіцієнти передачі фазочутливого підсилювача, підсилювача напруги і тиристорного перетворювача;

U_фп, U_п, U_d – вихідні напруги фазочутливого підсилювача, підсилювача напруги і тиристорного перетворювача.

Можна записати наступну систему рівнянь, яка описує двигун постійного струму з незалежним збудженням:

L_я·di_я/dt+r_я·i_я+c·ω= U_d;                                        (5)

М-М_с=J·dω/dt;                                                      (6)

c·ω=E_d;                                                                                                  (7)

c·i_я =М,(8)

          де L_я, r_я – індуктивність і активний опір якірного кола, i_я, E_d, ω – струм якоря, ЕРС і швидкість двигуна, c – коефіцієнт пропорційності між ЕРС і швидкістю, а також між моментом М і струмом якоря при незалежному потоку збудження, М_с – момент статичного навантаження, приведений до вала двигуна, J – сумарний момент інерції електропривода приведений до вала двигуна.

Рівняння передачі сигналу редуктором має наступний вигляд:

Θ_вих1=1/q ∫ω·dt               (9)

де q – передаточне число понижуючого редуктора.

          Проведемо аналіз нелінійних елементів (НЕ), які можливі в даній системі. Початковий сигнал редуктора буде відрізнятися від C_вых1 за рахунок нелінійності типу «люфт» в механіці цього виконуючого механізму. Тому реально на виході буде формуватися сигнал

Θ_вих= φ₁(Θ_вих1)                                                       (10)

З іншого боку, коло «фазочутливий підсилювача - тиристорний перетворювач» (ФЧУ-ТП) (рівняння (2) -(4)) може виконувати функцію обмеження значення струму шляхом формування нелінійності з зоною насичення. Відповідно

U_d= φ₂(δ)                                                               (11)

Якщо виразам (5) - (11) співвіднести відповідні передаточні функції, то структурна схема такої системи буде мати такий вид (мал. 2.2).

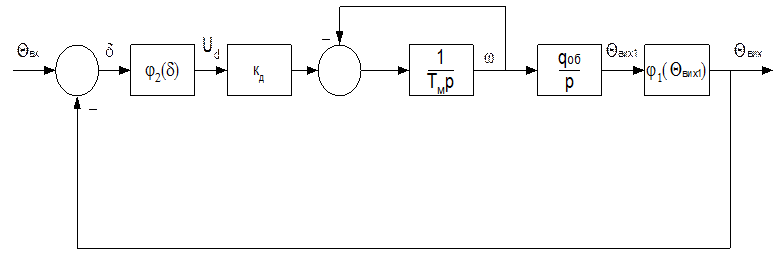
Малюнок 2.2 – Структурна схема слідкуюго електропривода (Т_я=L_я /r_я, Т_м=Jr_я /с²)

3.  Складаня системи рівнянь в нормальній формі Коші

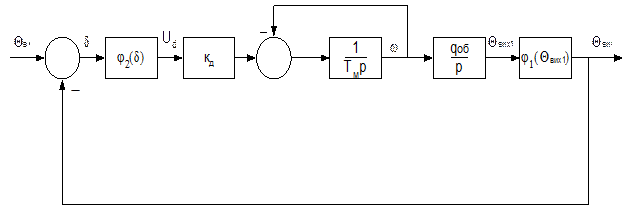При умові малого значення Т_я, що в більшості випадків відповідає реальній ситуації і відсутності зовнішнього статичного навантаження на двигун, структурна схема слідкуючого електропривода може бути зображена у вигляді схеми, показаної на мал. 3.1.

Малюнок 3.1 – Спрощена структурна схема слідкуючого електропривода (К_Д=1/c - коефіцієнт передачі двигуна q_об=1/q).

Якщо урахувати, що досліджується вільний рух системи, тобто спостерігається незмінне значення вхідного зовнішнього впливу (C_вх=0), а в якості основної координати х прийняти значення кута повороту осі двигуна

х=Θ_вих1                                               (12),

то в якості другої фазової координати зручно прийняти значення швидкості двигуна ω

y= ω                                                   (13),

що обумовлено можливістю зв’язати  їх між собою за допомогою простого виразу (9), тобто

x=q_об ∫y·dt                                                    (14)

або                                            dx/dt=q_об·y                                                    (15)

Вибір приведених вище визначальних параметрів електропривода в якості фазових координат, при умові вільного руху системи, дозволяє замінити дві присутні в системі нелінійності однією результуючою

U_d= φ₂(φ₁(-x))= φ(-x)                                             (16),

і дає можливість додатково зв’язати координати xі yтаким способом:

y= φ(-x)·к_д /(Т_мр+1)                                               (17),

          де р=d/dt - оператор диференціювання.

          Вираз (17) дозволяє записати ще одне рівняння з системи рівнянь форми Коші для розрахунку фазових траєкторій в координатах параметрів стану