Экстремальные системы автоматического управления

ЭКСТРЕМАЛЬНЫЕ САУ

В ряде процессов показатель качества, или эффективность, выражается в каждый момент времени функцией текущих координат системы. При этом система управления может считаться оптимальной, если она обеспечивает поддержание показателя качества в точке максимума.

Такие системы предназначены для управления объектами, которые не обладают монотонной зависимостью выходных параметров от входных. В них увеличение регулируемой величины может привести к одновременному уменьшению и увеличению регулируемого параметра, то есть объект обладает экстремальной статической характеристикой. (Рис. 1)

Значение регулируемого параметра, которое соответствует максимальной величине, называется оптимальным. Как правило, максимальная величина регулируемого параметра и соответствующее ей оптимальное значение регулирующего параметра заранее не известны или непредсказуемо изменяются под действием возмущений.

Чтобы использовать принцип обратной связи для управления объекта с экстремальной статической характеристикой, необходимо знать в какую сторону следует изменять регулирующий параметр для приведения регулируемого параметра к его максимальному значению, то есть знать, по какую сторону от точки б (Рис.1) находится точка отображающая состояние системы в данный момент. Для этого используют метод случайного поиска. Сначала производят небольшое пробное изменение регулирующего параметра, например, в сторону его увеличения, и выясняют, увеличивается или уменьшается при этом величина регулируемого параметра. Если она увеличивается, то регулирующий параметр продолжают изменять в ту же сторону, а если уменьшается - направление изменения регулирующего параметра меняют на противоположное.

Регулятор, который автоматически осуществляет пробные воздействия и определяет правильное направление изменения управляющего воздействия, называется экстремальным, а САУ с таким регулятором - экстремальной.

 Рассмотрим экстремальную САУ на примере процесса сжигания газа в топке.

рис

Пусть в некоторый момент времени расход воздуха и температура продуктов сгорания соответствуют точке а₀ (Рис. 2). После пробного шага - увеличения расхода воздуха - температура возрастает (а₁). Тогда регулятор вновь увеличит расход воздуха, что вызовет новое увеличение температуры (а₂). Таким образом, температура будет «шагами» приближаться к максимальному значению (б). Но после точки б при очередном увеличении расхода воздуха температура уменьшится (а₄). Регулятор отреагирует и уменьшит расход воздуха, то есть сделает шаг в противоположную сторону. При этом состояние системы будет отражаться точкой а₃, которая находится слева от точки б. Поэтому опять повторится шаг в сторону увеличения расхода воздуха и так далее. Возникнут колебания расхода воздуха и температуры возле точки искомого максимума. Такие колебания характерны для любой экстремальной системы, в которой происходит пошаговый поиск максимума регулируемого параметра.

Наличие колебаний в системе не позволяет достигнуть точного максимума, тем не менее они необходимы для нормальной работы систем. Рассмотрим работу САУ в случае, когда экстремальная характеристика объекта изменилась (точка б переместилась в точку б’). Прежнее значение расхода воздуха теперь не будет оптимальным, но узнать это можно лишь при очередном пробном изменении расхода воздуха, то есть при колебательном режиме работы. Таким образом, при очередном шаге из точки а₃ в точку а₄ температура возрастет (а₄’) и следующий шаг будет сделан в точку а₅’. Колебания в системе автоматически переместятся в окрестность нового максимума.

Поиск экстремума значительно усложняется, если показатель оптимальности зависит от нескольких переменных и изменяется несколькими регулирующими органами. Рассмотрим несколько методов для осуществления поиска.

Метод Гауса-Зайделя. Устанавливается очередность изменения координат х₁, х₂, х₃. Сначала делается шаг ∆х₁ по первой координате и выявляется знак вызванного этим шагом изменения показателя качества ∆I. Если шаг оказался неверным, надо изменить его направление и сделать последующие шаги (по той же координате) до тех пор, пока ∆I не станет равным нулю (или не изменит знак). Как только это произойдет, необходимо сделать ход по следующей координате ∆х₂ и продолжить процедуру аналогичным образом.

Метод градиента. На каждом шаге измеряются производные 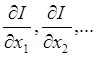; следующий шаг делается одновременно по всем координатам так, чтобы перемещение по каждой из них было пропорционально соответствующей производной. Тогда вектор суммарного перемещения будет направлен по градиенту. При непрерывном движении по градиенту траектория движения к экстремуму будет нормальной к линиям I=const.

Алгоритм экстремального управления по данному методу может быть сформулирован следующим образом: