Алгоритм обучения модели многомерного процесса в условиях неопределенности

.АЛГОРИТМ ОБУЧЕНИЯ МОДЕЛИ МНОГОМЕРНОГО ПРОЦЕССА

В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ

Гольцов А. С., ВПИ (филиал) ВолгГТУ

В теории управления сложились два основных подхода к описанию неопределенностей математической модели системы управления: стохастический и детерминированный. В стохастических моделях систем управления возмущающие воздействия считают случайными процессами с известными вероятностными характеристиками и используют принцип разделения (достоверной эквивалентности). Однако в задачах управления нелинейными объектами принцип разделения выполняется только в тех случаях, когда математические описания объекта управления (ОУ) и оптимальных траекторий перехода управляемых переменных в требуемое состояние известны с точностью до постоянных параметров, а возмущающие воздействия являются центрированными белыми гауссовскими шумами. Но в реальных ситуациях часто известны оптимальные траектории только для части переменных состояния ОУ, а для остальных переменных с помощью неравенств задано лишь множество допустимых траекторий перехода этих переменных в требуемое состояние. В этих случаях при синтезе систем оптимального управления возникают нелинейные двухточечные краевые задачи (ДКЗ), которые нельзя решать в реальном масштабе времени.

При синтезе систем управления в детерминированной (минимаксной) постановке предполагается, что возмущающие воздействия являются сигналами с ограниченной энергией, а математическое описание ОУ известно с точностью до постоянных (либо медленно изменяющихся) параметров, принадлежащих ограниченному множеству допустимых значений. Цель управления состоит в достижении наилучшего качества управления при наихудшей для выбранного управления реализации последовательности возмущающих воздействий. Структурную идентификацию передаточной функции замкнутой системы управления осуществляют методами - и - оптимизации. Оценивание переменных состояния и параметров математической модели системы управления осуществляют с помощью алгоритмов скоростного градиента, стохастической аппроксимации и другими методами. Однако эти методы синтеза системы управления можно применять только в линейной постановке задачи управления. Такая система управления не должна содержать интегрирующие звенья (а их включают в системы управления для обеспечения астатических свойств) и ограничения в форме неравенств на траектории перехода управляемых переменных в требуемое состояние. Кроме того, управляющие воздействия формируют в виде сигналов с ограниченной энергией, поэтому такие управляющие воздействия, как правило, нельзя применять в реальных задачах управления (абсолютная величина сигналов с ограниченной энергией с течением времени должна уменьшаться до нуля).

Решение задачи синтеза систем автоматического управления нелинейными процессами в условиях неопределенности предлагается выполнять с помощью регуляризации традиционной постановки задачи адаптивного управления. Предполагается, что математическая модель ОУ задана в пространстве состояний с помощью нелинейных уравнений:

;    ;

;    ;   :   ,

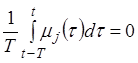где:  - вектор переменных состояния ОУ;  - вектор управляющих воздействий;  - вектор возмущающих воздействий на модель ОУ;  - вектор погрешностей задания начального состояния ОУ;  – вектор выходных переменных измерительных устройств (ИУ);  – вектор погрешностей измерений;  - предел допустимой погрешности j-го ИУ. Вектор  образован погрешностями математического описания скоростей изменения переменных состояния ОУ первым слагаемым правой части уравнения (1.1) и другими неконтролируемыми факторами. Возмущающие воздействия подлежат оцениванию в процессе управления. Кроме того, с помощью неравенств

;   ;   .

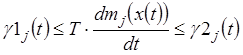задано множество допустимых траекторий перехода ОУ из начального состояния в конечное состояние.

С помощью В-сплайнов n-го порядка математическую модель изменения во времени оценок  вектора входных (обучающих) воздействий на модель ОУ можно задать в k-м интервале непрерывности сплайнов уравнением:

;  ;  ;  ,

где  - интервал непрерывности сплайнов;  - матрица известных финитных функций времени ;  - вектор параметров, подлежащих идентификации;  - вектор погрешностей аппроксимации, которые по условию состоятельности оценок  могут быть сигналами с ограниченной энергией.

Такую задачу оценивания переменных состояния ОУ можно теперь рассматривать как детерминированную задачу оптимального управления моделью ОУ: определить обучающие воздействия  на модель ОУ минимизацией регуляризованного по А.Н. Тихонову функционала обобщенной работы (РФОР). Для этого В скользящем временном окне (протяженностью ) сформируем скалярную переменную, образованную нормированной суммой средних абсолютных значений сигналов рассогласования:

.

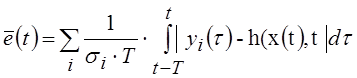Это дополнительное уравнение наблюдения содержит в явном виде информацию о прошлых состояниях объекта и его модели. Поэтому его необходимо включить в РФОР.

С помощью метода неопределенных множителей Лагранжа с последующим применением метода инвариантного погружения к возникающей ДКЗ получено решение этой задачи в виде регуляризованного алгоритма рекуррентного МНК. Полученный алгоритм отличается от традиционного алгоритма рекуррентного МНК тем, что осуществляет ПИ-регулирование обучающих воздействий на модель ОУ. Поэтому этот алгоритм формирует состоятельные оценки переменных состояния ОУ. Кроме того, показано, что полученный алгоритм асимптотически устойчив и формирует устойчивое решение задачи оценивания переменных состояния ОУ с произвольными возмущающими воздействиями. Требуемую близость к оптимальному решению можно обеспечить выбором значений параметра регуляризации и интервала непрерывности сплайнов.

Этот алгоритм был использован в проточном вискозиметре, предназначенном для непрерывного контроля вязкости нефтепродуктов, полимеров и других продуктов в процессе их производства.