Экстремальные системы автоматического управления, страница 2

а) накапливаются экспериментальные данные по входу х и по выходу у, по ним оцениваются величины математических ожиданий по входу М_х и по выходу М_у (блоки 2) и производится центрирование (блоки 3);

б) с использованием выражения

                     (*)

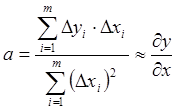где ∆у_i, ∆х_i - центрированные значения выходного и входного

            параметров объекта управления.

Вычисляются величины составляющих градиента по всем направлениям (блоки 6, 8, 9).

в) движение в сторону достижения экстремума осуществляется по выражению

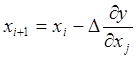
где x_i+1, ∆x_i - значения обобщенной координаты на i-той и i+1

             итерации;

    ∆ - величина приращения (обычно 2σ_х²);

     - составляющая градиента по j-тому направлению, вычисляемая по выражению (*).

рис

Алгоритм позволяет отслеживать дрейф оптимального режима и наносить управляющее воздействие, компенсирующее этот дрейф. Однако данный алгоритм не позволяет точно попасть в оптимум, а только следит за его перемещением.

Основным режимным параметром функционирования алгоритма является объем информации (m), накапливаемой для обеспечения расчетов по соотношению (*).

Точность вычислений возрастает при увеличении объема накопления и поэтому чем больше измерений, тем лучше. Но чем больше измерений, тем дольше происходит накопление информации, тем дальше оптимальный режим уплывает от рассчитанного, и тем больше возрастают потери при управлении. Поэтому существует компромисс между увеличением объема выборки и скорости дрейфа.

Разрешение данного компромисса и дает оптимальный режим функционирования алгоритма управления. Универсальность алгоритма позволяет рекомендовать его в качестве типового для многих технологических процессов. Особенно выгодно применение этого алгоритма в условиях больших (по амплитуде) изменений входных параметров для малоинерционных или без инерционных объектов.

Метод градиента дает идеальный путь к экстремуму, если поверхность (гиперповерхность) I (x₁,... х_n) является параболоидом вращения или сферой. Если сечения I=const отличны по форме от окружностей и вытянуты, то может оказаться более целесообразным использовать разные коэффициенты воздействий по производным . При сильно извилистых линиях, при наличии «оврагов» и «гребней» метод градиента становится малоцелесообразным.

Метод наискорейшего спуска. Сначала определяется направление градиента в начальной точке, а затем осуществляется прямолинейное движение по этому направлению до тех пор, пока не обратится в ноль (или не изменит знак) производная . Далее снова измеряется градиент и движение осуществляется по новому направлению, которое в случае остановки точно в точке с нулевым значением производной будет перпендикулярно предыдущему.

Случайный поиск. Резкое увеличение числа возможных комбинаций по перемещению регулирующих органов, из которых надлежит выбрать одну правильную, имеющую место при возрастании числа координат, привело к тому, что в ряде случаев введение элемента случайности в процедуру поиска сможет ускорить в среднем приближение к экстремуму.

Кроме регулярных пробных воздействий для осуществления поиска могут использоваться также случайные сигналы, создаваемые генераторами шумов или специальными фильтрами. Если система многомерна, то для каждой координаты следует выделять свою полосу частот шумовых сигналов. Рассмотрим «алгоритм наилучшей пробы», который заключается в следующем. Делается m случайных проб, каждая из которых вырабатывает случайным образом комбинации управляющих воздействий по всем координатам. При каждой пробе замеряется изменение показателя оптимальности ∆I. Проба с наилучшим результатом запоминается, и рабочий шаг делается в направлении вектора, давшего наилучший результата. Затем опять делается m проб и выбирается наилучший вектор из хранящихся в памяти векторов проб и так далее.

Системы экстремального регулирования могут использоваться как самостоятельно, так и в сочетании с системами, регулирующими по другому принципу.

Достоинства экстремальных САУ:

1. Экстремальное регулирование вне зависимости от применяемых процедур обеспечивает текущее отслеживание всех перемещений оптимума, что позволяет не делать проверки алгоритма на сходимость;
2. Алгоритмы экстремального регулирования выбираются из наиболее проверенных процедур вычислительной математики, следовательно, легко проверяемы и программируемы;
3. Экстремальное регулирование не требует знания математической модели объекта и использует гипотезу о том, что вблизи экстремума объект описывается квадратным уравнением (если вблизи экстремума объект описывается биквадратным уравнением, то экстремальное регулирование не применяется).

Законы управления экстремальных систем значительно сложнее типовых законов управления, поэтому экстремальные регуляторы реализуются, как правило, в цифровой форме.