Адаптация в автоматизированных системах – это процесс изменения параметров, структуры и управляющих воздействий на основе текущей информации с целью достижения определённого, обычно оптимального состояния системы при начальной неопределённости и изменяющихся условиях работы [62].
Одним из способов построения алгоритмов, применяемых в адаптивных системах управления, является использование теории оценивания и оптимальной фильтрации в качестве математической базы. Теории оценивания и оптимальной фильтрации были сформулированы в 50-60 годах ХХ века и описаны в работах Н.Винера [17], Р. Беллмана [6], Р. Калмана [34], А.А. Фельдбаума [59], Р. Бьюси [34] и Острёма [44]. Обобщённые результаты теории оценивания приведены в работах Э. Сейджа и Дж. Мелса [53, 54], Р. Изермана [32]. На базе данных работ впоследствии были разработаны рекуррентные алгоритмы оптимального управления, описанные в работах Фрадкова [42], Цыпкина [62, 63], Фомина [60, 61], Поляка [22], Растригина [51], Граничина [22, 23] и других авторов [43, 67, 68].
В настоящее время методика исследования оценок, получаемых рекуррентными алгоритмами оценивания и оптимальной фильтрации, приобрела в целом законченный вид. И в настоящее время работы [1, 3, 7, 21, 24, 25, 31, 40, 42, 48, 50, 58, 64, 70, 71, 72, 73, 75, 77, 80, 82, 84, 86, 87, 88] направлены на применение теории оптимального управления к конкретным динамическим объектам. На примере данных работ видно, что возможно построение адаптивных систем управления, основанных на рекуррентных методах оценивания и оптимальной фильтрации, которые будут обеспечивать оптимальное управление в соответствии с выбранными критериями оптимальности и качества. Одним из способов определения оптимальных критериев управления сложным динамическим объектом является минимизация функционала обобщённой работы [19, 20, 21, 38].
При этом следует отметить, что применение данных алгоритмов для ЭВМ даёт результаты при использовании математических моделей процессов и объектов, описанных в пространстве состояний.
В общем случае, адаптивная система, показанная на рисунке 1.4, содержит устройство управления, реализующее один из фундаментальных принципов управления, и устройство адаптации, взаимодействующее с устройством управления [19]. Непосредственно управляет объектом устройство управления, а устройство адаптации предназначено для обеспечения его оптимальной настройки. Система автоматического управления в этом случае имеет два иерархических уровня.
Устройство адаптации состоит из обучаемой модели объекта управления и блока настройки регулятора. Последний на основании результатов идентификации параметров объекта управления и внешней среды обеспечивает соответствующее изменение параметров устройства управления или его структуры и алгоритма управления.
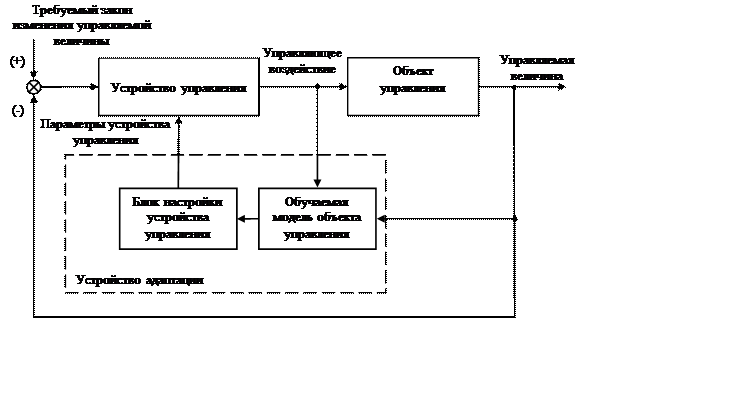
Рисунок 1.4 – Структурная схема адаптивной системы управления
Устройство адаптации включается в цепь обратной связи и реагирует также на изменение управляемой переменной. Таким образом, можно сформулировать пять взаимосвязанных задач, решение которых даст возможность построить оптимальную систему.
Задача управления. Рассматривается система с заданной связью между входным управляющим воздействием и состояниями системы. Требуется найти управление, меняющее состояние так, чтобы была достигнута некоторая заданная цель.
Задача оценки состояния. Рассматривается известная система со случайным входным воздействием и шумом измерения так, что измеренный выходной сигнал представляет собой искаженное состояние. Известны законы распределения шума устройства и шума измерения, требуется найти “наилучшую” оценку истинного состояния системы по известному выходному сигналу.
Задача стохастического управления. Задача стохастического управления может быть получена путем объединения первых двух задач. Требуется определить такое управление, чтобы выходное состояние системы изменялось желаемым образом. Присутствуют шум устройства и шум измерений. Известны законы распределения этих шумов, требуется найти наилучшую оценку состояния системы по наблюдаемому выходному состоянию, прежде чем можно будет определить “наилучшее” управление.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.