Анализ систем управления активной мощностью печей сопротивления для производства карбида кремния, страница 5

где

x − фракция (объём) карбида кремния;

,− начальное и текущее газосодержание шихты;

, − начальное и текущее значение теплоёмкости шихты;

,− начальное и текущее значение коэффициента теплопроводности шихты;

,  − начальное и текущее значение плотности шихты;

,, − теплоёмкость, теплопроводность и плотность карбида кремния.

Предполагается, что фракция  карбида кремния зависит от фракции газов SiO₂, расчёт которой осуществляется по уравнению:

,

(1.8)

где

R − скорость реакции карбидообразования;

 − коэффициент диффузии;

K − параметр, зависящий от площади диффузии. 

Граничными условиями являются уравнение тепловыделения на графитовом керне и у стенки печи сопротивления:

, ,

(1.9)

где

I − ток, протекающей через керн;

− электрическое сопротивление печи;

r₁ − радиус керна печи;

r₂  − радиус стенки печи;

L − длина керна;

Q − теплота, теряющаяся через кирпичную изоляционную стенку и стальное основание печи.

Описанная математическая модель позволяет рассчитывать радиальный профиль температуры в печи, фракцию карбида кремния в реальном времени. Для решения математической модели необходимы измерения начальных значений коэффициентов для шихты, электрического сопротивления керна, коэффициента теплопроводности шамотного изоляционного кирпича, температуры стенки печи. При большом количестве печей, имеющих разную степень износа изоляции и электродов, их характеристики будут значительно отличаться. Отдельные компоненты шихты (песок, нефтяной кокс) могут закупаться у разных поставщиков, поэтому их физические свойства будут также отличаться. Вследствие этого измерение всех необходимых параметров модели является затруднительным.   

Математическая модель [28] содержит уравнения теплопроводности в частных производных для ванны печи и для изоляционной стенки:

(1.10)

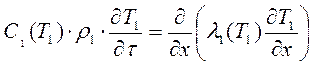 − для стенок печи;

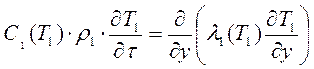 − для пода печи;

где:

, ,  − значения теплоёмкости для шихты, стенок печи и выделяемых газов;

,, −  плотность шихты, материала стенок печи и выделяемых газов;

, − коэффициенты теплопроводности шихты и стенок печи;

− скорость газовой фильтрации;

 −  температура газов;

 − начальная концентрация шихтовых компонентов;

,  − стехиометрическое соотношение и молекулярный вес шихтовых компонентов;

 − тепловой эффект от реакции образования карбида кремния;

 − степень превращения исходных компонентов шихты;

x,y − координаты сечения печи.

Преимущество предложенной модели заключается в том, что описываемая подвижная печь сопротивления является точным аналогом печей, используемых на предприятии ОАО «Волжский абразивный завод». Математическая модель позволяет рассчитывать двухмерное распределение температуры по сечению печи. Однако для решения предложенной модели необходимо измерять значения физических коэффициентов шихты, скорость и температуру выделяемых газов, что очень сложно реализовать на рассматриваемом производстве.

Описанные модели содержат множество коэффициентов тепловых характеристик шихты, точное определение которых затруднительно. К тому же, свойства компонентов шихты изменяются в процессе плавки при постепенном превращении части шихты в карбид кремния. Возмущения, связанные с особенностями конструкции конкретной печи, а также со сложными химическими процессами внутри печи, являются неконтролируемыми.

Из приведенных математических моделей видно, что процесс образования карбида кремния в печи сопротивления является довольно сложным процессом, который сопровождается химическими реакциями превращения части шихты в карбид кремния и меняющейся во времени площадью реакционной зоны. Использование одной из перечисленных выше математических моделей без возможности измерения температуры печи и знания множества начальных параметров шихты (теплоемкость, теплопроводность, плотность) не может дать приемлемого результата.

Однако для задачи управления мощность печи может быть использована математическая модель, составленная по методу «вход-выход», рассматривая объект управления (печь сопротивления) как «черный ящик». Такой подход получил широкое распространение в адаптивных системах автоматического управления, использующих обучаемую математическую модель объекта управления в цепи в обратной связи [19].