Определение возможностьи применения железобетонных шпал типа 2Ш27-Ат800СБ при обращении четырехосных грузовых вагонов с повышенными осевыми нагрузками до 230 кН со скоростью 80 км/час в кривых

3. Расчетно-конструктивная часть.

Требуется определить возможность применения железобетонных шпал типа 2Ш27-Ат800СБ при обращении четырехосных грузовых вагонов с повышенными осевыми нагрузками до 230 кН со скоростью 80 км/час в кривых. Размеры шпалы и расчетные схемы приведены на листе 4.

3.1. Определение вертикальных и горизонтальных сил, действующих на шпалу.

Расчетные характеристики вагона:

-статическая нагрузка колеса                                                       Р_ст=115 кН;

-диаметр колеса                                                                              d=0,95 м;

-вес необрессоренных частей экипажа, отнесенный к колесу  q=11 кН;

-приведенная к колесу жесткость рессор                                    ж=2 кН/мм;

-расстояние между смежными осями тележки                            l₁=1,80 м;

-предельно допускаемая глубина ползуна на поверхности катания колеса а₁=0,67 мм.

Расчетные характеристики пути:

-рельсы Р50 с приведенным износом 6 мм, I_y=1813 см⁴  = 1,813∙10^-5 м⁴, I_z=377 см⁴ = =0,377∙10^-5 м⁴, β=1; число шпал на 1 км в кривой 2000, l=0,5 м; балласт щебеночный, γ=1; рельсовое скрепление типа СБ-65 с упругой прокладкой толщиной 7 мм.

Модуль упругости подрельсового основания u=110 МПа, при горизонтальном изгибе u_z=63 МПа, при кручении рельса u_φ=315 кН/рад.

Коэффициент относительной жесткости рельса и подрельсового основания будет равен:

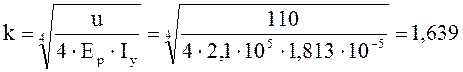 м^-1

Максимальный прогиб рессор:

 мм.

Максимальное усилие возникающее от колебания надрельсовой части экипажа:

 кН.

Средняя нагрузка колеса на рельс:

 кН.

Среднеквадратичное отклонение усилий:

 кН.

Среднеквадратичное отклонение динамической нагрузки колеса на рельс от сил инерции необрессоренных масс при прохождении колесом плавной изолированной неровности пути:

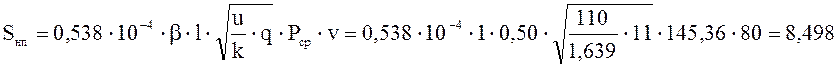кН.

Среднеквадратичное отклонение динамической нагрузки колеса на рельс от сил инерции необрессоренных масс вследствие наличия непрерывных неровностей на поверхности катания колес:

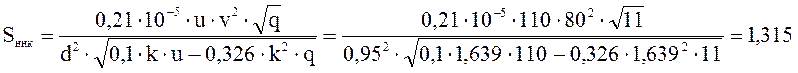 кН.

Среднеквадратичное отклонение динамической нагрузки колеса на рельс от сил инерции необрессоренных масс из-за наличия плавных изолированных неровностей на поверхности катания колес:

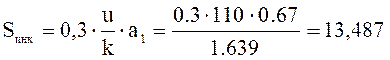 кН.

Среднеквадратичное отклонение динамической нагрузки колеса на рельс, вызванное неравномерностью передачи нагрузки отдельным шпалам вследствие наличия в пути рядом с расчетной шпалой неработающих шпал:

 кН.

По таблицам для k∙l₁=1,82∙1,80=3,28 находится η=-0,0424.

Эквивалентная нагрузка, учитывающая влияние смежной оси вагонной тележки:

η∙P_ср=-0,0424∙145,36= -6,163 кН.

Расчетная максимальная нагрузка колеса на рельс:

 кН.

Для четырехосного грузового вагона при а_нп=0,7 м/с²:

-рамная сила Z_p=31,5+26∙а_нп=31,5+26∙0,7=49,70 кН;

-боковая сила Н=54+25∙а_нп=54+25∙0,7=71,50 кН.

Поперечные силы с учетом коэффициентов горизонтальной динамичности:

Z_дин=Z_p∙(1+0.0024∙v)=49,7∙(1+0,0024∙80)=59,24 кН;

Н_дин=Н_р∙(1+0,003∙v)=71,50∙(1+0,003∙80)=88,66 кН.

Дополнительная вертикальная нагрузка на наружный рельс и разгрузка внутреннего: 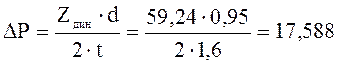 кН.

Расчетная вертикальная динамическая нагрузка с учетом перегрузки от действия рамной силы:  кН.

Вертикальная сила давления рельса на шпалу:

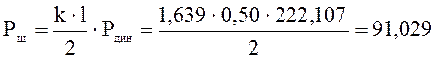 кН.

Коэффициент относительной жесткости в горизонтальной плоскости:

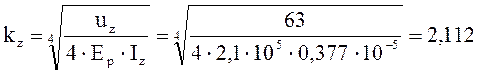м^-1;

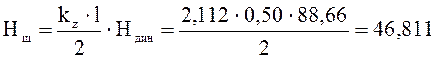 кН.

Боковая сила Н_ш , приложенная на уровне подошвы рельса, создает в подрельсовом сечении шпалы изгибающий момент:

 кН.

Схема сил и моментов, действующих на шпалу, представлена на листе 4.

Вертикальную нагрузку считаем распределенной на уровне нейтральной оси подрельсовой части шпалы на длине е:

м.

Распределенную нагрузку представим в виде:

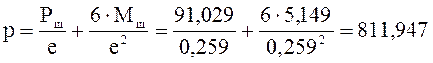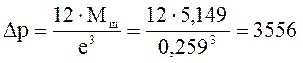кН/м,

кН/м.

3.2. Определение изгибающих моментов, поперечных сил и прогибов (давлений на балласт).

Расчетная схема шпалы показана на листе 4. Примем коэффициент постели с=13∙10⁴ кН/м³.

Расчетные характеристики шпалы на первом (подрельсовом участке):

b₁=0,270 м; I_red1=1,449∙10^-4 м⁴; Е_b=3,25∙10⁷ кН/м².

Оснавная характеристика уравнения прогиба шпалы как балки на упругом основании:

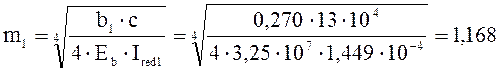 м^-1.

Для конца первого, подрельсового участка: z=l₁∙m₁=1,05∙1,168=1,227 м;

z-a=m₁∙(l₁-a)=1,168∙(1,05-0,41)=0,748 м; z-β=m₁∙(l₁-b)=1,168∙(1,05-0,68)=0,432 м.

Для этих аргументов находим значения следующих функций:

A_x=cos(x)∙ch(x);                        B_x=0,5∙(sin(x)∙ch(x)+cos(x)∙sh(x));

C_x=0,5∙sin(x)∙sh(x);                  D_x=0,25∙(sin(x)∙ch(x)-cos(x)∙sh(x))