6. Быстронатекающая ползучесть для бетона подвергнутого тепловой обработке при натяжении арматуры на упоры:
Rbp=0,7∙Rb=0,7∙22,308=15,615 МПа;
σsp,I=σsp-(σ1+σ2+σ3+σ4+σ5)=570-(17,1+81,25+0+0+0)=471,65 МПа;
Ns=Asp∙σsp,I=4.524∙10-4∙471,65∙103=213 кН;
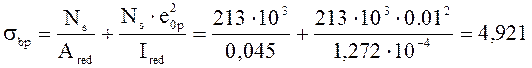 Мпа;
Мпа;
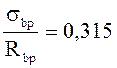 < 0,25+0,025∙Rbp=0,64;
< 0,25+0,025∙Rbp=0,64;
σ6=0,85∙40∙σbp/Rbp=0,85∙40∙0,315=10,716 МПа.
Все первые потери:
σI=σ1+σ2+σ3+σ4+σ5+σ6=109,06 МПа.
Вторые потери (II)
7. Релаксация напряжений арматуры:
σ7=0.
8. Усадка бетона:
σ8=40 МПа.
9. Ползучесть бетона:
Ns=Asp∙(σsp-σI)= 4,524∙10-4∙(570-109,06)∙103=209 МПа;
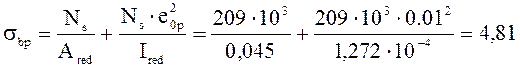 МПа;
МПа;
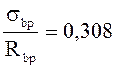 < 0,75
< 0,75
σ6=0,85∙150∙σbp/Rbp=0,85∙150∙0,308=39,27 МПа
После всех потерь напряжения в арматуре на уровне ее центра тяжести будут
σII=σ7+σ8+σ9=0+40+39,27=79,27 МПа;
σsp=570-(σI+σII)=570-(109,106+79,27)=381,664 МПа.
Общая сила предварительного обжатия:
Ns=Asp∙σsp=4,524∙10-4∙381,664∙103=172,661 кН.
Установившиеся предварительные напряжения в бетоне:
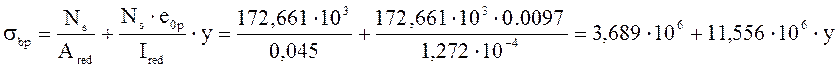
Расчет трещинностойкости бетона в растянутой зоне:
По нижнему краю сечения (растянутая зона) y=0 ур=уred
σbp=3,689+11,556∙0,087=4,73 МПа;
Наименьший предельный момент по трещинностойкости бетона:
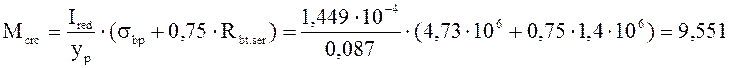 кН∙м.
кН∙м.
Расчет выносливости сечения:
По верхнему краю сечения (сжатая зона) y=0,193 м
yсж=yred-y=0,087-0,193=-0,106 м;
σbp=3,689-11,556∙0,106=2,467 МПа;
Определим подбором с интерполяцией коэффициент γb1:
γb1=0,77, 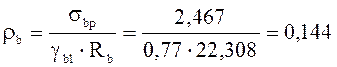 ;
;
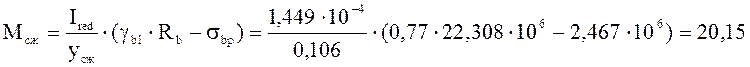 кН∙м.
кН∙м.
На уровне нижнего, наиболее растянутого ряда арматуры у=0,045 м
уа=уred-0,045=0,087-0,045=0,042 м;
σbp=3,689-11,556∙0,042=4,177 МПа;
σs.min=σsp-α’∙σbp=381,664-10∙4,177=339,892 МПа;
Подбором с интерполяцией принимаем γs3=0,57,
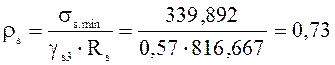 ;
;
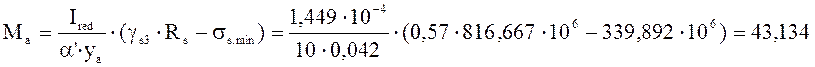 кН∙м.
кН∙м.
Расчет предельной поперечной силы по условию трещинностойкости на нейтральной оси приведенного сечения шпалы:
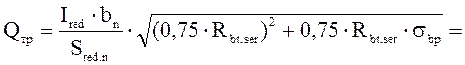
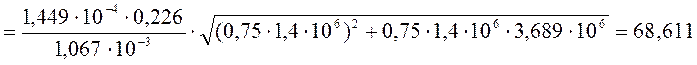 кН
кН
Расчет сечения по середине шпалы производим аналогично расчету по подрельсовому сечению.
Геометрические характеристика поперечного сечения шпалы на среднем участке при a’=10:
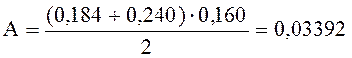 м2;
м2;
![]() м2;
м2;
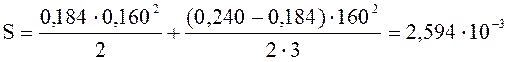 м3;
м3;
![]() м3;
м3;
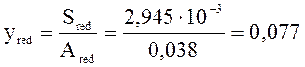 м;
м;
![]() м;
м;
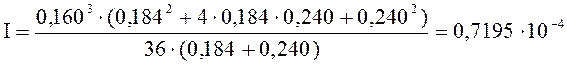 м4;
м4;
![]()
![]() м4;
м4;
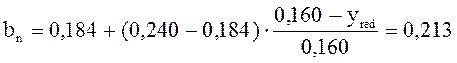 м;
м;
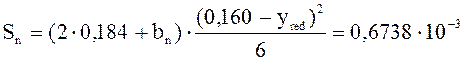 м3;
м3;
![]()
![]() м3.
м3.
Установившиеся предварительные напряжения в бетоне:
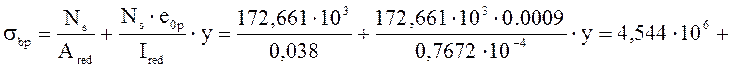
![]()
Расчет трещинностойкости бетона в растянутой зоне:
По верхнему краю сечения (растянутая зона) у=0,160 м.
yp=yred-y=0,077-0,160=-0,083 м;
σbp=4,554+2,029∙0,083=4,66 МПа;
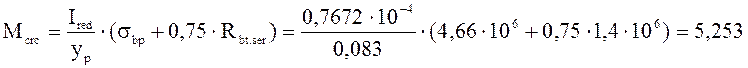 кН∙м.
кН∙м.
Расчет выносливости сечения:
По нижнему краю сечения (сжатая зона)
y=0;
yсж=yred=0,077 м;
σbp=4,554+2,029∙0,077=4,336 МПа;
Определим подбором с интерполяцией:
γb1=0,82, 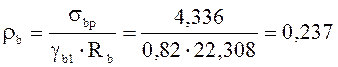 ;
;
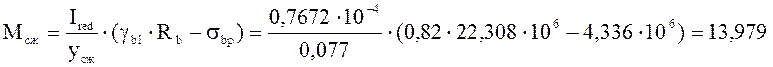 кН∙м.
кН∙м.
На уровне верхнего, наиболее растянутого ряда арматуры
у=0,110 м, уа=уred-у=0,077-0,110=-0,033 м;
σbp=4,554+2,029∙0,033=4,559 МПа;
σs.min=σsp-α’∙σbp=381,664-10∙4,559=336,074 МПа;
Подбором с интерполяцией принимаем γs3=0,57,
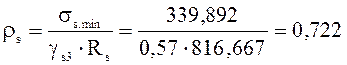 ;
;
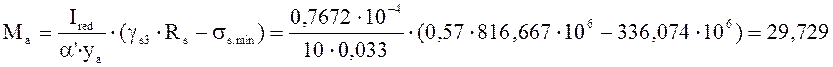 кН∙м
кН∙м
3.4. Анализ полученных результатов.
Полученные результаты сведем в таблицу 3.1.
Таблица 3.1 –Результаты расчета.
|
Предельный изгибающий момент, кН∙м по условию |
По середине подрельсовой площадки |
По середине шпалы |
||
|
-выносливости бетона в сжатой зоне |
20,15 |
Действующий момент 6,67 кН∙м |
-13,98 |
Действующий момент -5,135 кН∙м |
|
-выносливости наиболее растянутой арматуры |
43,13 |
-29,73 |
||
|
-трещинностойкости бетона в растянутой зоне |
9,55 |
-5,25 |
||
|
Предельная поперечная сила, кН, по условию трещинностойкости на нейтральной оси приведенного сечения |
68,61 |
Действующая поперечная сила 32,14 кН |
- |
- |
Сопоставление наибольших эксплуатационных моментов с наименьшими предельными моментами по выносливости и трещинностойкости бетона в расчетных сечениях шпалы показывает, что при данных характеристиках пути и подвижного состава применение железобетонных шпал типа 2Ш27-Ат800СБ может быть допущено.
Давление на шпалы балласт под концом шпалы σбс=334 кПа, посередине подрельсовой площадки - σбс=214,5 кПа. Нормативное давление равно σбс.норм=0,325 МПа.
Сопоставление показывает, что напряжение в балласте в подрельсовом сечении не превышает допускаемых на щебеночный балласт от вагонных нагрузок. напряжение в балласте под концом шпалы выше допускаемых. Это не может служить запретом для применения шпал в этих условиях, но вызовет остаточные деформации балластного слоя под концами шпал.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.